Algorithm For the first example: s=1:{bestcost(A1×A2),bestcost(A2×A3),bestcost(A3× A4)} s=2:{bestcost(A1×A2×A3),bestcost(A2×A3×A4)} ■fori=1t0ns=3:{bestcost(a1×A2×A3×A4} ▣C(i,)=0 fors =1 to n-1 //s:step length for i=1 ton-s Best cost of Best cost of ■j=i+S A;×…XAK Ak+1X…×Aj C(i,j)=mingC(i,k)+C(k +1,+mi-1mkmii<k<j return C(1,n) Cost of X×Y,where X=A:X…XAk, Y=Ak+1×…×A i j=i+s 11
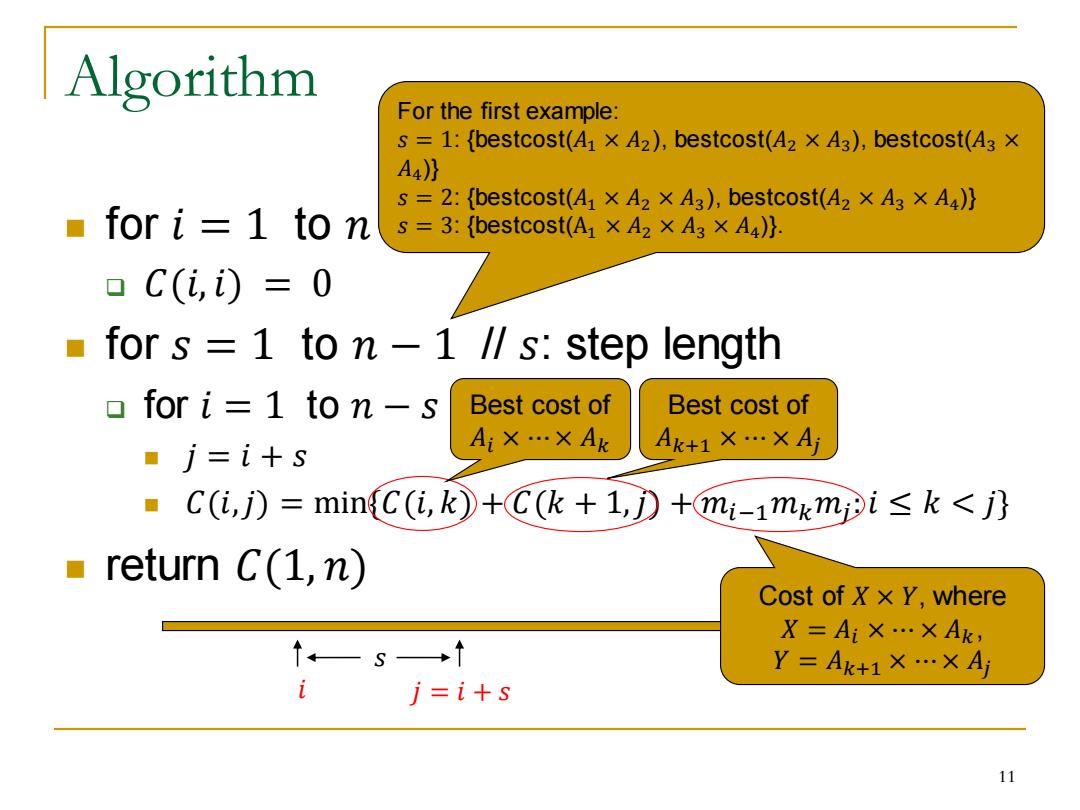
Algorithm ◼ for 𝑖 = 1 to 𝑛 ❑ 𝐶(𝑖, 𝑖) = 0 ◼ for 𝑠 = 1 to 𝑛 − 1 // 𝑠: step length ❑ for 𝑖 = 1 to 𝑛 − 𝑠 ◼ 𝑗 = 𝑖 + 𝑠 ◼ 𝐶(𝑖,𝑗) = min{𝐶(𝑖, 𝑘) + 𝐶(𝑘 + 1,𝑗) + 𝑚𝑖−1𝑚𝑘𝑚𝑗 : 𝑖 ≤ 𝑘 < 𝑗} ◼ return 𝐶(1, 𝑛) 𝑖 𝑗 = 𝑖 + 𝑠 𝑠 Best cost of 𝐴𝑖 × ⋯ × 𝐴𝑘 Best cost of 𝐴𝑘+1 × ⋯ × 𝐴𝑗 Cost of 𝑋 × 𝑌, where 𝑋 = 𝐴𝑖 × ⋯ × 𝐴𝑘, 𝑌 = 𝐴𝑘+1 × ⋯ × 𝐴𝑗 For the first example: 𝑠 = 1: {bestcost(𝐴1 × 𝐴2 ), bestcost(𝐴2 × 𝐴3), bestcost(𝐴3 × 𝐴4)} 𝑠 = 2: {bestcost(𝐴1 × 𝐴2 × 𝐴3 ), bestcost(𝐴2 × 𝐴3 × 𝐴4)} 𝑠 = 3: {bestcost(A1 × 𝐴2 × 𝐴3 × 𝐴4)}. 11

Complexity for i=1 to n ▣C(i,)=0 for s=1 to n-1 //s:step length)terations for i=1 ton-s ■j=i+s -0(1) C(i,j)=min{C(i,k)+C(k+1,j)+mi-1mkmj:i<k <j return C(1,n) -0(n) Total:0(n2)×0(n)=0(n3) Much better than the exponential! 12
Complexity ◼ for 𝑖 = 1 to 𝑛 ❑ 𝐶(𝑖, 𝑖) = 0 ◼ for 𝑠 = 1 to 𝑛 − 1 // 𝑠: step length ❑ for 𝑖 = 1 to 𝑛 − 𝑠 ◼ 𝑗 = 𝑖 + 𝑠 ◼ 𝐶(𝑖,𝑗) = min{𝐶(𝑖, 𝑘) + 𝐶(𝑘 + 1,𝑗) + 𝑚𝑖−1𝑚𝑘𝑚𝑗 : 𝑖 ≤ 𝑘 < 𝑗} ◼ return 𝐶(1, 𝑛) ◼ Total: 𝑂 𝑛 2 × 𝑂(𝑛) = 𝑂(𝑛 3 ) ❑ Much better than the exponential! 12 Θ(𝑛 2 ) iterations –𝑂(𝑛) –𝑂(1)

Optimal value vs.optimal solution We've seen how to compute the optimal value using dynamic programming. What if we want an optimal solution? The order of matrix multiplication. 13
Optimal value vs. optimal solution ◼ We’ve seen how to compute the optimal value using dynamic programming. ◼ What if we want an optimal solution? ❑ The order of matrix multiplication. 13

Problem 2:longest increasing subsequence 14
Problem 2: longest increasing subsequence 14

Problem 2:longest increasing subsequence A sequence of numbers a1,a2,...,an ▣Eg:5,2,8,6,3,6,9,7 A subsequence:a subset of these numbers taken in order oai,ai2,,ai,where1≤i<i2<…<ij≤n An increasing subsequence:a subsequence in which the numbers are strictly increasing ▣Eg:5,2,8,6,3,6,9,7 Problem:Find a longest increasing subsequence. 15
Problem 2: longest increasing subsequence ◼ A sequence of numbers 𝑎1,𝑎2,… , 𝑎𝑛 ❑ Eg: 5, 2, 8, 6, 3, 6, 9, 7 ◼ A subsequence: a subset of these numbers taken in order ❑ 𝑎𝑖1 , 𝑎𝑖2 , …, 𝑎𝑖𝑗 , where 1 ≤ 𝑖1 < 𝑖2 < ⋯ < 𝑖𝑗 ≤ 𝑛 ◼ An increasing subsequence: a subsequence in which the numbers are strictly increasing ❑ Eg: 5, 2, 8, 6, 3, 6, 9, 7 ◼ Problem: Find a longest increasing subsequence. 15