
Macromechanical Analysis of a Lamina 71 AD=(A+D) A'D=VAy+(x,y+△)-(x,y+[u(x,y+△y)-(x,y, AD=△y. 2.10a,b) Substituting the preceding expressions of Equation(2.10)in Equation(2.9), △y △y Using definitions of partial derivatives, Ev=ay' (2.11) because au1, dy dy for small displacements. A normal strain is positive if the corresponding length increases;a normal strain is negative if the corresponding length decreases. The shearing strain in the x-y plane,Yv is defined as the change in the angle between sides AB and AD from 90.This angular change takes place by the inclining of sides AB and AD.The shearing strain is thus defined as Yy=01+02, (2.12) 2006 by Taylor Francis Group,LLC
Macromechanical Analysis of a Lamina 71 AD = Δy. (2.10a,b) Substituting the preceding expressions of Equation (2.10) in Equation (2.9), . Using definitions of partial derivatives, (2.11) because for small displacements. A normal strain is positive if the corresponding length increases; a normal strain is negative if the corresponding length decreases. The shearing strain in the x–y plane, γxy is defined as the change in the angle between sides AB and AD from 90°. This angular change takes place by the inclining of sides AB and AD. The shearing strain is thus defined as (2.12) AD AQ QD ′ ′ = ( ′ ′) + ( ′ ′) , 2 2 AD y v x y y v x y ux y ′ ′ = + +− + [ (, ) (, ) Δ Δ ] [(, 2 + − Δy ux y ) (, )] , 2 y y vx y y vx y y ε = + + − → lim ( , ) ( , )} / Δ Δ 0 Δ 1 2 2 1 ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ + ⎡ + − ⎣ ⎢ ⎤ ⎦ ⎥ ⎧ ⎨ ⎪ ⎩ ⎪ ⎫ ux y y ux y y 2 (, ) (, ) Δ Δ ⎬ ⎪ ⎭ ⎪ − 1 y v y u y ε = + ∂ ∂ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ + ∂ ∂ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ⎡ ⎣ ⎢ ⎢ ⎤ 1 2 2 2 1 / ⎦ ⎥ ⎥ − 1 y v y ε = ∂ ∂ , ∂ ∂ << u y 1, ∂ ∂ << v y 1, xy γ = + θ θ 1 2, 1343_book.fm Page 71 Tuesday, September 27, 2005 11:53 AM © 2006 by Taylor & Francis Group, LLC
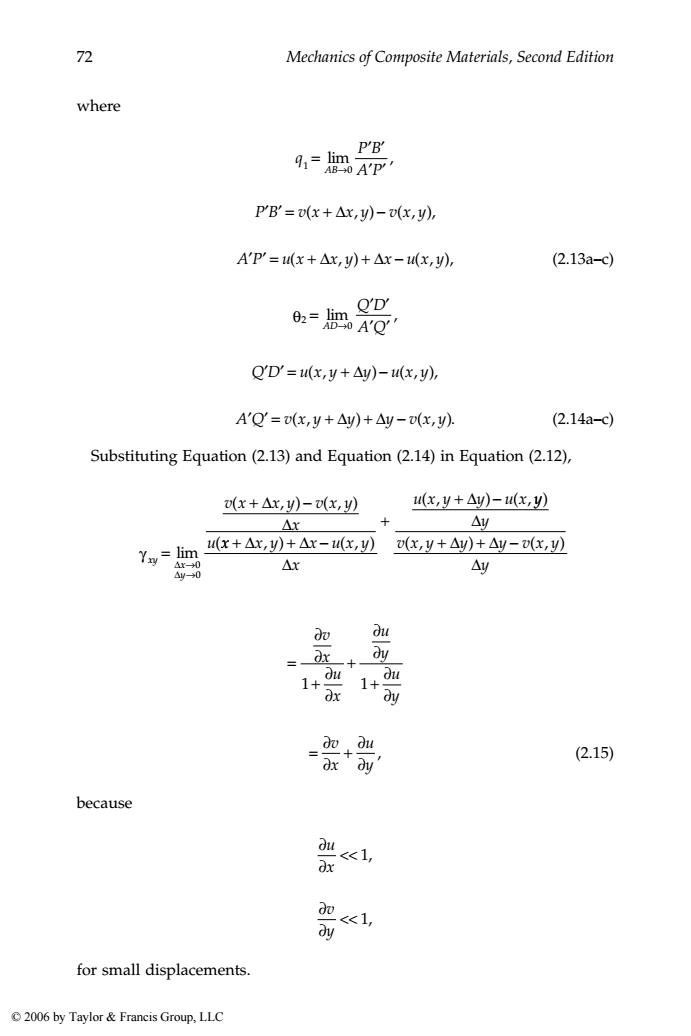
72 Mechanics of Composite Materials,Second Edition where P'B' 9 AP P'B'=v(x+Ax,y)-v(x,y), A'P'=(x+△x,y)+△r-(x,y), (2.13a-c) QD 02=A Q'D'=u(x,y+Ay)-u(x,y), A'Q=ox,y+△y)+△y-x,y) (2.14a-c) Substituting Equation(2.13)and Equation(2.14)in Equation(2.12), (x+△x,y)-(x,y) (x,y+△y)-(x,y) △x + △y Yay=lim u(x+△x,y)+△x-1u(x,y) x,y+△y)+△y-(x,y) △x0 △x △y △y-0 dv ou + dy du 1+ 1+ du dx ay dv du ax dy (2.15) because du 221, ax w ay for small displacements. 2006 by Taylor Francis Group,LLC
72 Mechanics of Composite Materials, Second Edition where (2.13a–c) (2.14a–c) Substituting Equation (2.13) and Equation (2.14) in Equation (2.12), (2.15) because for small displacements. 1 0 q P B AB A P = ′ ′ → ′ ′ lim , PB v x x y v x y ′ ′ =+ − ( , ) ( , ), Δ AP ux x y x ux y ′ ′ = + +− ( , ) ( , ), Δ Δ 2 0 θ Q D AD A Q = ′ ′ → ′ ′ lim , QD ux y y ux y ′ ′ = +− ( , ) ( , ), Δ AQ v x y y y v x y ′ ′ = + +− ( , ) ( , ). Δ Δ vx x y vx y x u xy x y γ = + − → → lim ( , ) (, ) ( Δ Δ Δ Δ 0 0 x x y x ux y x ux y y ux + +− + + − Δ Δ Δ Δ , ) (, ) (, ) (, y y vx y y y vx y y ) (, ) (, ) Δ Δ Δ Δ + +− = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ v x u x u y u y 1 1 = ∂ ∂ + ∂ ∂ v x u y , ∂ ∂ << u x 1, ∂ ∂ << v y 1, 1343_book.fm Page 72 Tuesday, September 27, 2005 11:53 AM © 2006 by Taylor & Francis Group, LLC

Macromechanical Analysis of a Lamina 73 The shearing strain is positive when the angle between the sides AD and AB decreases;otherwise,the shearing strain is negative. The definitions of the remaining normal and shearing strains can be found by noting the change in size and shape of the other sides of the infinitesimal cuboid in Figure 2.7 as do dw Yy=zdy ow ou Y=axoz ow E2= (2.16a-c) Example 2.1 A displacement field in a body is given by u=105(x2+6y+7xy) 0=10-5yz) 0=105(xy+yz2) Find the state of strain at (x,y,z)=(1,2,3). Solution From Equation(2.8), du e,20x =o(e+6y+7》 =10-5(2x+7z =10-5(2×1+7×3 =2.300×10-4. 2006 by Taylor Francis Group,LLC
Macromechanical Analysis of a Lamina 73 The shearing strain is positive when the angle between the sides AD and AB decreases; otherwise, the shearing strain is negative. The definitions of the remaining normal and shearing strains can be found by noting the change in size and shape of the other sides of the infinitesimal cuboid in Figure 2.7 as (2.16a–c) Example 2.1 A displacement field in a body is given by u = 10–5(x2 + 6y + 7xy) v = 10–5(yz) w = 10–5(xy + yz2) Find the state of strain at (x,y,z) = (1,2,3). Solution From Equation (2.8), . yz v z w y γ = ∂ ∂ + ∂ ∂ , zx = w x + u z γ , ∂ ∂ ∂ ∂ z w z ε = ∂ ∂ . ∈ = ∂ ∂ x u x = ∂ ∂ ( ) ( ) + + − x 10 6 7 x y xz 5 2 = + ( ) − 10 2 7 5 x z = ×+× ( ) − 10 2 1 7 3 5 = × − 2 300 10 4 . 1343_book.fm Page 73 Tuesday, September 27, 2005 11:53 AM © 2006 by Taylor & Francis Group, LLC

74 Mechanics of Composite Materials,Second Edition From Equation(2.11), dv ey-dy ((y)) =105(2) =10-5(3) =3.000×10-5」 From Equation(2.16c), w e.20z =0y+》 -105(2yz) =10-5(2×2×3) =1.2×104. From Equation(2.15), u+地 =yx =品ok+6y+7a+品o6 2006 by Taylor Francis Group,LLC
74 Mechanics of Composite Materials, Second Edition From Equation (2.11), . From Equation (2.16c), . From Equation (2.15), ∈ = ∂ ∂ y v y = ∂ ∂ ( ) ( ) − y 10 yz 5 = ( ) − 10 5 z = ( ) − 10 3 5 = × − 3 000 10 5 . ∈ = ∂ ∂ z w z = ∂ ∂ ( ) ( ) + − z 10 xy yz 5 2 = ( ) − 10 2 5 yz = ×× − 10 2 2 3 5 ( ) = × − 1 2 10 4 . γ xy u y v x = ∂ ∂ + ∂ ∂ = ∂ ∂ ( ) ( ) + + + ∂ ∂ ( ) ( ) − − y x y xz x 10 6 7 10 yz 52 5 1343_book.fm Page 74 Tuesday, September 27, 2005 11:53 AM © 2006 by Taylor & Francis Group, LLC

Macromechanical Analysis of a Lamina 75 =10-5(6)+10-5(0) =6.000×10-5. From Equation(2.16a), dv ow Yy=dz dy =足o(+oy*+g》 =105(y)+10-5(x+2) =105(2)+105(1+32) =1.2×104. From Equation(2.16b), =品10(y+yr2月+是0-(r+6y+7z》 =105(y)+105(7x) =10-5(2)+10-5(7×1 =9.000×10-5. 2.2.3 Elastic Moduli As mentioned in Section 2.2.2,three equilibrium equations are insufficient for defining all six stress components at a point.For a body that is linearly 2006 by Taylor Francis Group,LLC
Macromechanical Analysis of a Lamina 75 . From Equation (2.16a), . From Equation (2.16b), . 2.2.3 Elastic Moduli As mentioned in Section 2.2.2, three equilibrium equations are insufficient for defining all six stress components at a point. For a body that is linearly = ( ) + ( ) − − 10 6 10 0 5 5 = × − 6 000 10 5 . γ yz v z w y = ∂ ∂ + ∂ ∂ = ∂ ∂ ( ) ( ) + ∂ ∂ ( ) ( ) + − − z yz y 10 10 xy yz 5 52 = ( ) + + ( ) − − 10 10 5 52 y xz = ( ) + + ( ) − − 10 2 10 1 3 5 52 = × − 1 2 10 4 . γ zx w x u z = ∂ ∂ + ∂ ∂ = ∂ ∂ ( ) ( ) + + ∂ ∂ ( ) ( ) + + − − x xy yz z 10 10 6 7 x y xz 5 2 52 = ( ) + ( ) − − 10 10 7 5 5 y x = ( ) + × ( ) − − 10 2 10 7 1 5 5 = × − 9 000 10 5 . 1343_book.fm Page 75 Tuesday, September 27, 2005 11:53 AM © 2006 by Taylor & Francis Group, LLC