
第三章水动力学基础 二、欧拉法(流场法) 欧拉法是把充满液体质点的空间作为研究对象,不用跟踪 每个质点,而是把注意力集中在考察分析水流中的水质点在通过 固定空间点时的速度、压强的变换情况,来获得整个液体运动的 规律。由于欧拉法是以流动的空间作为研究对象,所以通常把液 体流动所占据的空间称为流场。此发亦称流场法。 在直角坐标系中,各运动要素是空间坐标x,y,z和时间变 量t的函数。空间点的坐标x,y,z,t称为欧拉变量。 则流速场u可表示为:u=u(x,y,z,) 设流速u在x、y、z三个坐标轴方向的投影是u,山,山,则流速场可 写成: 稻 KRNN
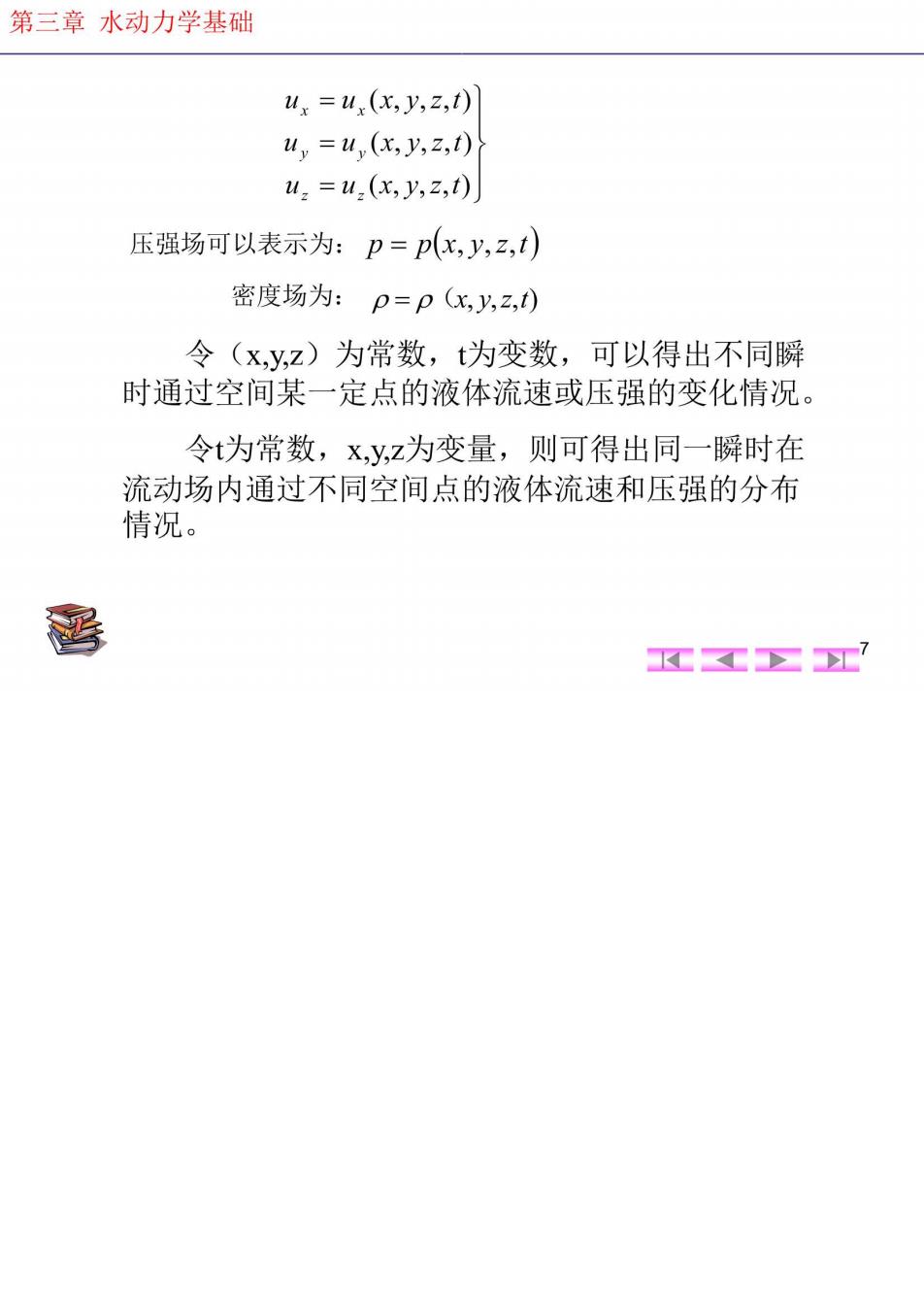
第三章水动力学基础 ux=u,(x,y,z,t) u=u (x,y,2,1) u.=u.(x,y,z,t) 压强场可以表示为:p=p(x,y,z,t) 密度场为:p=p(x,y,z,) 令(x,y,z)为常数,t为变数,可以得出不同瞬 时通过空间某一定点的液体流速或压强的变化情况。 令t为常数,x,y,z为变量,则可得出同一瞬时在 流动场内通过不同空间点的液体流速和压强的分布 情况。 西 KC工Σ江

第三章水动力学基础 加速度应是速度对时间的全导数。因此,根据复合函数求导法则并考虑到 dr =4,可得加速度在空间坐标x,y,z方向的分量为 dt ou, dt ot 0z du。 ou, a,= dt ot u. dt ot O: 8z 当地加速度 迁移加速度 善第一项为当地加速度,后三项为迁移加速度·工
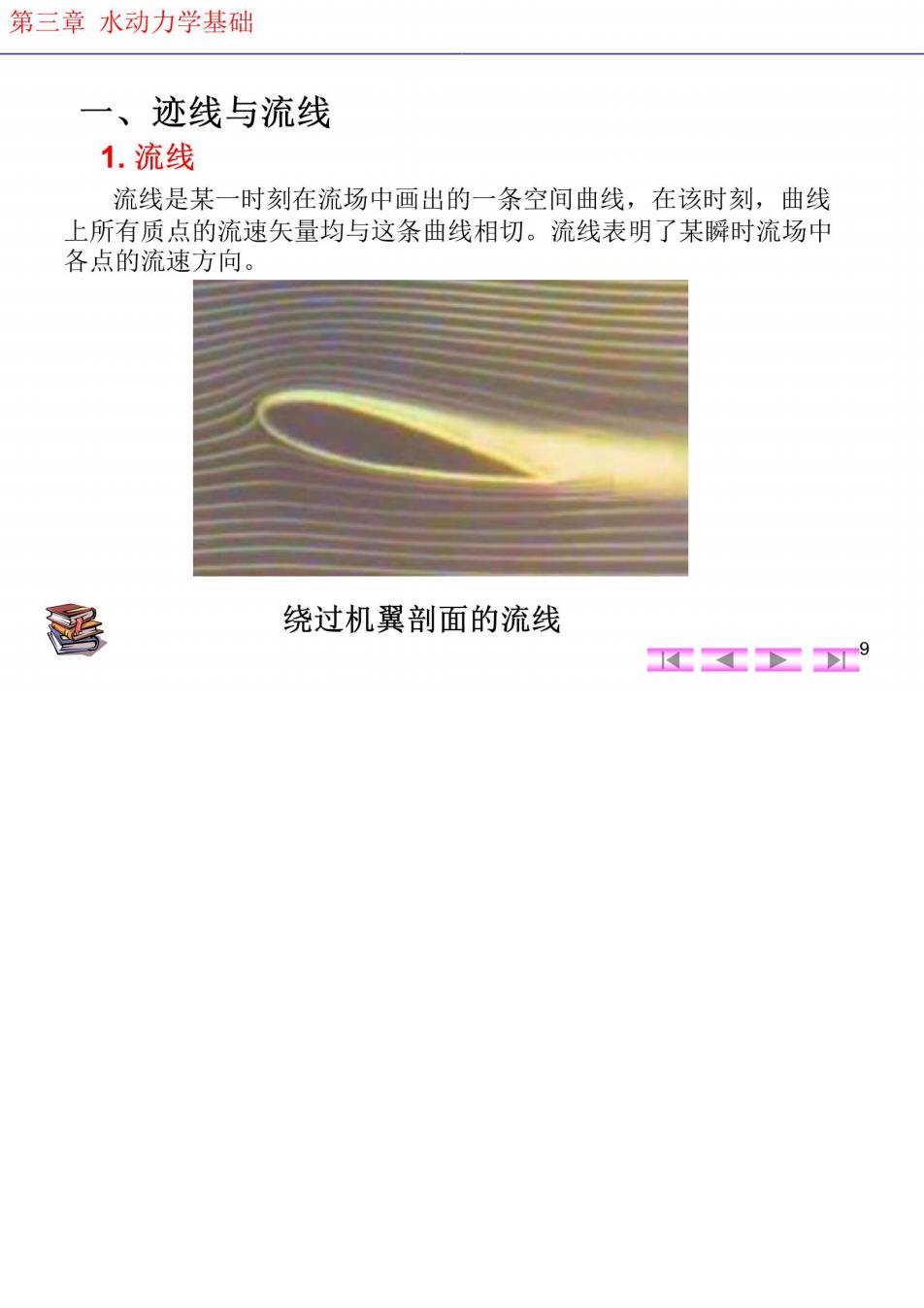
第三章水动力学基础 一、迹线与流线 1.流线 流线是某一时刻在流场中画出的一条空间曲线,在该时刻,曲线 上所有质点的流速矢量均与这条曲线相切。流线表明了某瞬时流场中 各点的流速方向。 移 绕过机翼剖面的流线 K工Σ9

第三章水动力学基础 绕叶片的流线 绕突然缩小管道的流线