
重点课程运筹学案例集 样就显得更合理了。(3)为了公平,所有的交易者都应公平对待。 另外,对应任意正数C,的规划的最优解其实与严格小于1的入,对应的行和列的组成的 线性方程D1=A的解是相同的。换句话说,就是规划()的最优基本可行解与C,的取值无 关,只要C,保持正值(证明过程见附录)。这可用含两个交易者的问题来解释:这个图表明 可行域的形状和最优基本可行解会根据两个交易者或其中 一个交易者是否有完全清偿能力而 变动。四种可能的解在图中画出来:(1)两个交易者都不破产,即由两个交易者对应的不等 式约束交于c。在这种情况下,唯一的极点a对应最优的基本可行解,在该点入=l,几2=1: (2)两个交易者都破产,这时解用两条虚线的交点b给出,最优解为入<1入2<1:(3) 交易者1破产,而交易者2不破产,这时点c代表了最优基本可行解,入<1几2=1:(4) 交易者2破产,而交易者1不破产,这时入=1几2<1,点d代表了最优基本可行解。 最优点: a)两个交易者都不会破产 (b)两个交易者都会破 (c)仅交易者2会破产 (d)仅交易者1会破产 元≤1 该图还画出当两个交易者都不破产时的目标函数对应的线。显然无论在前述哪种情形下, 对应的最优可行解并不随C,的取值而改变。所以只要目标函数的系数保持正值,他们不对最 优解产生影响。规划(P)包含有N个变量,N个由(6)给出的不等式约束。N个(7)给出的 上界约束和(8)给出的非负约束。假设C,=1,我们用IBw的数学规划软件包PSX370在 BW4341型计算机上求解出了该规划:(1)(6)中第i行的松弛变量X,的值,它表示交易者 最后剩下的资产的价值。若该值大于0,则表示相应的交易者能偿还债务,不至于破产。(2) 交易者在不超过上界的约束下的最大的债务清偿比率入, 不会破产的交易者可以由入,=和X>0确认出来。他们的资产可调整为 a,=☑,一X,这里☑为他们用于偿债的那部分资产。求解出新的线性方程D2=A以后, 结果入将与(P)的最优基本可行解一致。 第16页共66页
重点课程运筹学案例集 第 16 页 共 66 页 样就显得更合理了。(3)为了公平,所有的交易者都应公平对待。 另外,对应任意正数 C j 的规划的最优解其实与严格小于 1 的 j 对应的行和列的组成的 线性方程 D = A 的解是相同的。换句话说,就是规划(P)的最优基本可行解与 C j 的取值无 关,只要 C j 保持正值(证明过程见附录)。这可用含两个交易者的问题来解释:这个图表明 可行域的形状和最优基本可行解会根据两个交易者或其中一个交易者是否有完全清偿能力而 变动。四种可能的解在图中画出来:(1)两个交易者都不破产,即由两个交易者对应的不等 式约束交于 e。在这种情况下,唯一的极点 a 对应最优的基本可行解,在该点 1, 1 1 2 = = ; (2)两个交易者都破产,这时解用两条虚线的交点 b 给出,最优解为 1, 1 1 2 ;(3) 交易者 1 破产,而交易者 2 不破产,这时点 c 代表了最优基本可行解, 1, 1 1 2 = ;(4) 交易者 2 破产,而交易者 1 不破产,这时 1, 1 1 2 = ,点 d 代表了最优基本可行解。 最优点: (a)两个交易者都不会破产 (b)两个交易者都会破产 (c)仅交易者 2 会破产 (d)仅交易者 1 会破产 2 1 该图还画出当两个交易者都不破产时的目标函数对应的线。显然无论在前述哪种情形下, 对应的最优可行解并不随 Ci 的取值而改变。所以只要目标函数的系数保持正值,他们不对最 优解产生影响。规划(P)包含有 N 个变量,N 个由(6)给出的不等式约束。N 个(7)给出的 上界约束和(8)给出的非负约束。假设 C =1 i ,我们用 IBM 的数学规划软件包 MPSX370 在 IBM4341 型计算机上求解出了该规划;(1)(6)中第 i 行的松弛变量 xsi 的值,它表示交易者 最后剩下的资产的价值。若该值大于 0,则表示相应的交易者能偿还债务,不至于破产。(2) 交易者在不超过上界的约束下的最大的债务清偿比率 i 。 不会破产的交易者可以由 =1 i 和 x 0 Si 确认出来。他们的资产可调整为 ai ai xSi = − ,这里 ai 为他们用于偿债的那部分资产。求解出新的线性方程 D = A 以后, 结果 i 将与(P)的最优基本可行解一致

重点课程运筹学案例集 我们用一个含有四个交易者的例子来解释一下1,到【,内的交易者的构成。这个例子同时 说明如何用方程(2)来调整【,和1,内的交易者的资产。调整后的2和I3内的交易者的资产 将用来归结为 一个2-交易者的线性规划模型(如图一所描述) 「83-42-5-151 10 -9 65 -40-15 设:D= -74-2345-20 0= 85 00050」 L30 交易者1,2,3,4分别属于1,2,和4。他们所有的债务和等于所有的债权和,正 好形成一个封闭的系统。 求解这个例子时,能很容易地看出只有交易者3是不会破产的交易者。而交易者4是没 有任何债权的肯定会破产的。所以入=L九,=30/50=0.6。用公式(2)对交易者1的资 产进行调整a=24(原有的10+从交易者3收回的应收款项5+从交易者4收回的60%的应收教 项15*60%)。同样交易者2的资产=52。为了确定入,和九2,我们归结出下面的线性模型。 值得提出的是原来的包含四个交易者的模型会产生相同的结果。 max+ 831-42元2≤34, S.4. -911+6512≤52, 1≤1,元≤1, 元20,1220. 该规划的解为几=0.746,入2=0.903。图1中的点b就代表了该最优解。这两个交易者都会 破产。而前面又已知道交易者4也将破产,所以这个例子只有一个交易者3不会破产。破产 者的资产加上他们实际收回的应收款项用于还债,交易者1只还74.6%。而交易者2与交易者 4分别只还90.3%和60%。 在这个例子里,注意到一开始4个交易者共有128元资产。到最后,交易者1,2和4均 只有0元,而交易者3将拥有全部的128元。交易者3将先将其所欠交易者1和2的债务还 清(分别为5元和40元),这时他从原有85元剩下40元。当P解决后,他从交易者1那收 回55.2元(74元的74.6%),再从交易者2那里收▣20.8元(23元的90.3%),从交易者4那 里收回12元(20元的60%)。这样他最后拥有128元。 这个简单的例子说明了我们是怎样用LP来解决问题的。这样的方法使大规模的问题也简 单了一些。在第四部分,我们提出了一个10个交易者的例子来解释另一些补充的应用问题。 3.按资产类型的清偿比例 到目前为止,讨论己进行到可以将不会破产的交易者从会破产的交易者中确认出来,并 确认每个交易者的债务清偿比率。换句话说,我们已经知道为了将债务危机消除,每一个债 务应为他所欠的每一科威特元支付多少元。但是,这还保留了一个问题需要解决。既然每个 交易者所有的资产包括许多类型(如股票,债券,现金不动产等),这些资产具有不同的风险 那末应如何组合这些金融工具来支付给 债 人呢?正由于资 产的价值仅代表现在名义 的市场价值,我们认为只有按与债务人资产组合相同的比例来分配他们的资产给他们的债权 人才是公平的。 当考虑到某些资产的所有权会在各交易者之间转移,而他的质量和形式都是无法预知时, 第17页共66页
重点课程运筹学案例集 第 17 页 共 66 页 我们用一个含有四个交易者的例子来解释一下 I1 到 I4 内的交易者的构成。这个例子同时 说明如何用方程(2)来调整 I2 和 I3 内的交易者的资产。调整后的 I2 和 I3 内的交易者的资产 将用来归结为一个 2-交易者的线性规划模型(如图一所描述) 设: = − − − − − − − − − = 30 85 3 10 0 0 0 50 74 23 45 20 9 65 40 15 83 42 5 15 D Q 交易者 1,2,3,4 分别属于 I3,I2,I1 和 I4。他们所有的债务和等于所有的债权和,正 好形成一个封闭的系统。 求解这个例子时,能很容易地看出只有交易者 3 是不会破产的交易者。而交易者 4 是没 有任何债权的肯定会破产的。所以 1, 30/50 0.6 3 4 = = = 。用公式(2)对交易者 1 的资 产进行调整 a1=24(原有的 10+从交易者 3 收回的应收款项 5+从交易者 4 收回的 60%的应收款 项 15*60%)。同样交易者 2 的资产 a2=52。为了确定 1 和 2 ,我们归结出下面的线性模型。 值得提出的是原来的包含四个交易者的模型会产生相同的结果。 0, 0. 1, 1, 9 65 52, 83 42 34, . . max 1 2 1 2 1 2 1 2 1 2 − + − + st 该规划的解为 0.746, 0.903 1 2 = = 。图 1 中的点 b 就代表了该最优解。这两个交易者都会 破产。而前面又已知道交易者 4 也将破产,所以这个例子只有一个交易者 3 不会破产。破产 者的资产加上他们实际收回的应收款项用于还债,交易者 1 只还 74.6%。而交易者 2 与交易者 4 分别只还 90.3%和 60%。 在这个例子里,注意到一开始 4 个交易者共有 128 元资产。到最后,交易者 1,2 和 4 均 只有 0 元,而交易者 3 将拥有全部的 128 元。交易者 3 将先将其所欠交易者 1 和 2 的债务还 清(分别为 5 元和 40 元),这时他从原有 85 元剩下 40 元。当 LP 解决后,他从交易者 1 那收 回 55.2 元(74 元的 74.6%),再从交易者 2 那里收回 20.8 元(23 元的 90.3%),从交易者 4 那 里收回 12 元(20 元的 60%)。这样他最后拥有 128 元。 这个简单的例子说明了我们是怎样用 LP 来解决问题的。这样的方法使大规模的问题也简 单了一些。在第四部分,我们提出了一个 10 个交易者的例子来解释另一些补充的应用问题。 3.按资产类型的清偿比例 到目前为止,讨论已进行到可以将不会破产的交易者从会破产的交易者中确认出来,并 确认每个交易者的债务清偿比率。换句话说,我们已经知道为了将债务危机消除,每一个债 务应为他所欠的每一科威特元支付多少元。但是,这还保留了一个问题需要解决。既然每个 交易者所有的资产包括许多类型(如股票,债券,现金不动产等),这些资产具有不同的风险, 那末应如何组合这些金融工具来支付给每一个债权人呢?正由于资产的价值仅代表现在名义 的市场价值,我们认为只有按与债务人资产组合相同的比例来分配他们的资产给他们的债权 人才是公平的。 当考虑到某些资产的所有权会在各交易者之间转移,而他的质量和形式都是无法预知时

重点课程运筹学案例集 这个问题就会变的复杂起来。于是,有必要设计一个系统,通过它分配交易者的资产(假如 有m种),而且使分配给他的债权人资产的构成比例与他的资产构成比例相同,这样,就能达 到公正的要求。这可以通过解决交易者间关于每种类型的资产k的债务纠纷米完成,我们为 每种类型的资产设计了一个联立的方程来解决所有交易者之间的纠纷。假设某交易者的资产 ☑,等于其所有各类资产的价值和。向量A用矩阵可表示为: A=AI+A2 +Am 9 其中 A= ☑为交易者i拥有k类资产的价值量。 将(6)中不等式换为等式,并替换A,得到一个线性等式系统: D2=A+A2+…+Am 所以 =D-A+D-A+…+D-A (10) 设 九=DA, (k=1,2,m) 那末 =++…+ (12) 等式(12)说明一个交易者的债务清偿比率等于他所拥有的各种资产的债务清偿比率之 和。而且D显然不依赖于各种资产类型k。所以,只需要求得D的逆阵并将D乘上m 个资产向量A来得到m个2x的值。 可把前面所讲的根据资产类型来分配债务清偿包含在一个稍大LP内以直接提供每种资产 k的飞:。这可通过重新改写约束(6)完成,每个约束将向量2:作为变量,向量A作为右 边值。应付款项卫和应收款项r,无论资产类型都保持一样。再另给参数阝来表示不破 的交易者用完各种资产的优先级。这样,可扩展计划P,以求出2k=(w,2k,…): (P) ax∑x∑YC,B,4 s1.p,4-∑n2t≤ak,i=1,2,N,k=l,2,m ∑ks1, i=1,2,N 2体≥0, i=1,2,N,k=1,2,m. 第18页共66页
重点课程运筹学案例集 第 18 页 共 66 页 这个问题就会变的复杂起来。于是,有必要设计一个系统,通过它分配交易者的资产(假如 有 m 种),而且使分配给他的债权人资产的构成比例与他的资产构成比例相同。这样,就能达 到公正的要求。这可以通过解决交易者间关于每种类型的资产 k 的债务纠纷来完成。我们对 每种类型的资产设计了一个联立的方程来解决所有交易者之间的纠纷。假设某交易者的资产 ai 等于其所有各类资产的价值和。向量 A 用矩阵可表示为: A=A1+A2+………..+Am (9) 其中 = nk k k k a a a A ... 2 1 aik 为交易者 i 拥有 k 类资产的价值量。 将(6)中不等式换为等式,并替换 A,得到一个线性等式系统: D = A + A + + Am ...... 1 2 所以 D A D A D Am 1 2 1 1 1 ...... − − − = + + + (10) 设 , ( 1,2,......, ) 1 k = D Ak k = m − (11) 那末 = + + + m ...... 1 2 (12) 等式(12)说明一个交易者的债务清偿比率等于他所拥有的各种资产的债务清偿比率之 和。而且 D −1 显然不依赖于各种资产类型 k。所以,只需要求得 D 的逆阵并将 D −1 乘上 m 个资产向量 Ak 来得到 m 个 k 的值。 可把前面所讲的根据资产类型来分配债务清偿包含在一个稍大LP内以直接提供每种资产 k 的 k 。这可通过重新改写约束(6)完成,每个约束将向量 k 作为变量,向量 Ak 作为右 边值。应付款项 pi 和应收款项 rij 无论资产类型都保持一样。再另给参数 k 来表示不破产 的交易者用完各种资产的优先级。这样,可扩展计划 P,以求出 ( , ,....... ) k = 1k 2k nk : 0, 1,2,..., , 1,2,..., . 1, 1,2,..., . . , 1,2,..., , 1,2,..., ( ) max 1 1, 1 1 i N k m i N st p r a i N k m P C i k m k i k j k i k N i i k j j i i j k i k N i N k i i = = = − = = = = = =

重点课程运筹学案例集 规划(P)含有Nm个向量,N(m+1)个约束和Nm个约束,而规划(P)仅含有N个变 量,N个约束,N个上界限制和N个非负限制,所以规(P,)比(P)要大,求解也要复杂 我们可以有两种选择来求解(P,),即直接求解和依据等式(1)按步求解(P)。 在结果中的水可用来计算实际的交易者的各种资产的债权债务清偿数。这个方法保证了 个唯一而且公平的资产支付方式和解决所有交易者间债务问题的方法, 模型的应用:一个有具体数字的解释性例子 到目前为止,本文给出了三个模型:线性规划模型(P),债务清偿分配的线性系统等式 (I1),以及扩展后的线性规划模型(P),有两种选择可以应用这些模型。一是用(P)将 不会破产的交易者从破产的交易者中分辨出来,如果所有的交易者都要破产,那么按等式(11〉 来资产类型非债务清偿比率。但如果某些交易者不会破产,那我们就要根据一些事先定好的 偏好系统按资产类型调整不会破产的交易者的资产价值。在当前的问题里,资产被分为四类: 现金及KSE资产,不动产从不会破产的交易者那里收可的债权,以及黑市的股票。政府提定 的资产优先级为现金,不动产,债权和黑市公司股票。 调整后的新的资产向量用在等式(I1)中计算按资产类型分配的债务清偿比例。我们也 可以一开始就用(P)一次性求解。下面这个包含有10个交易者的数值性例子,就解释了 前一种方法。债务矩阵D和资产向量Q定义如下: [28-2-4-2-1-20-1-2-2] [20 -1220-3 -6-2 -4-3-5--2 10 -3-40150-10-8-1-2-4-5-2 60 -2-15-10 800 -250-10 -4-2 7 D= 0-10-12-960-5 -6-5-3-2 18 -6-12-15-2-7100 -20 -6 -2 0= 80 -1 -4 -10-12-2-250 -2 -3-1 9 4 -8-20 -4 -2-10 -3 60 -3 -3 2 0 0 0 00000 400 -1 -2 -3 -10 -2 -1 -2 -220 22 矩阵满足下列条件:(1)所有对角线元素为正:(2)所有非对角线元素非正:(3)对每个交易 者,债务和严格小于债权之和。 依据四种交易者类型的划分原则,这10个交易者可如下划分:(1)不会破产者 12=f[i=120<28.36>281.i=518<60.70>601.i=680<100.132>1001: (3)拥有债权但肯定会破产的交易剔==21020,38202801,=360<150135≈150,75>01=47 80,75<80,68>0].=719<50,46<50,37>0182<60,59<60,57>0(4没有债权肯定会破产的交易 I4={i=940>5,R=0: 以上划分严格遵照债务债权及现有资产间的不等式关系。可以用它在现实生活中划分交易 者类型,求解方程Dλ=Q,可以部分地完成划分。解为: 第19页共66页
重点课程运筹学案例集 第 19 页 共 66 页 规划( Pk )含有 Nm 个向量,N(m+1)个约束和 Nm 个约束,而规划(P)仅含有 N 个变 量,N 个约束,N 个上界限制和 N 个非负限制,所以规划( Pk )比(P)要大,求解也要复杂。 我们可以有两种选择来求解( Pk ),即直接求解和依据等式(11)按步求解(P)。 在结果中的 k 可用来计算实际的交易者的各种资产的债权债务清偿数。这个方法保证了 一个唯一而且公平的资产支付方式和解决所有交易者间债务问题的方法。 模型的应用:一个有具体数字的解释性例子 到目前为止,本文给出了三个模型:线性规划模型(P),债务清偿分配的线性系统等式 (11),以及扩展后的线性规划模型( Pk ).有两种选择可以应用这些模型。一是用(P)将 不会破产的交易者从破产的交易者中分辨出来,如果所有的交易者都要破产,那么按等式(11) 来资产类型非债务清偿比率。但如果某些交易者不会破产,那我们就要根据一些事先定好的 偏好系统按资产类型调整不会破产的交易者的资产价值。在当前的问题里,资产被分为四类: 现金及 KSE 资产,不动产从不会破产的交易者那里收回的债权,以及黑市的股票。政府规定 的资产优先级为现金,不动产,债权和黑市公司股票。 调整后的新的资产向量用在等式(11)中计算按资产类型分配的债务清偿比例。我们也 可以一开始就用( Pk )一次性求解。下面这个包含有 10 个交易者的数值性例子,就解释了 前一种方法。债务矩阵 D 和资产向量 Q 定义如下: − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − = 1 2 3 1 0 2 1 2 2 20 0 0 0 0 0 0 0 0 40 0 4 8 20 4 2 10 3 60 3 3 1 4 10 12 2 2 50 2 3 1 6 12 15 2 7 100 2 0 6 2 0 10 12 9 60 5 6 5 3 2 2 15 10 80 0 25 0 10 4 2 3 40 150 10 8 1 2 4 5 2 1 220 3 6 2 4 3 5 2 2 28 2 4 2 1 2 0 1 2 2 D = 22 5 2 9 80 18 7 60 10 20 Q 矩阵满足下列条件:(1)所有对角线元素为正:(2)所有非对角线元素非正:(3)对每个交易 者,债务和严格小于债权之和。 依据四种交易者类型的划分原则,这 10 个交易者可如下划分:(1)不会破产者 I2={[i=1|20<28,36>28],[i=5|18<60,70>60],[i=6|80<100,132>100]}; (3)拥有债权但肯定会破产的交易I3={[i=2|10<220,38>22028>0],[i=3|60<150,135<150,75>0],[i=4|7 <80,75<80,68>0],[I=7|9<50,46<50,37>0],[I=8|2<60,59<60,57>0]};(4)没有债权肯定会破产的交易 I4={i=9|40>5,R=0}; 以上划分严格遵照债务债权及现有资产间的不等式关系。可以用它在现实生活中划分交易 者类型,求解方程 Dλ=Q,可以部分地完成划分。解为:
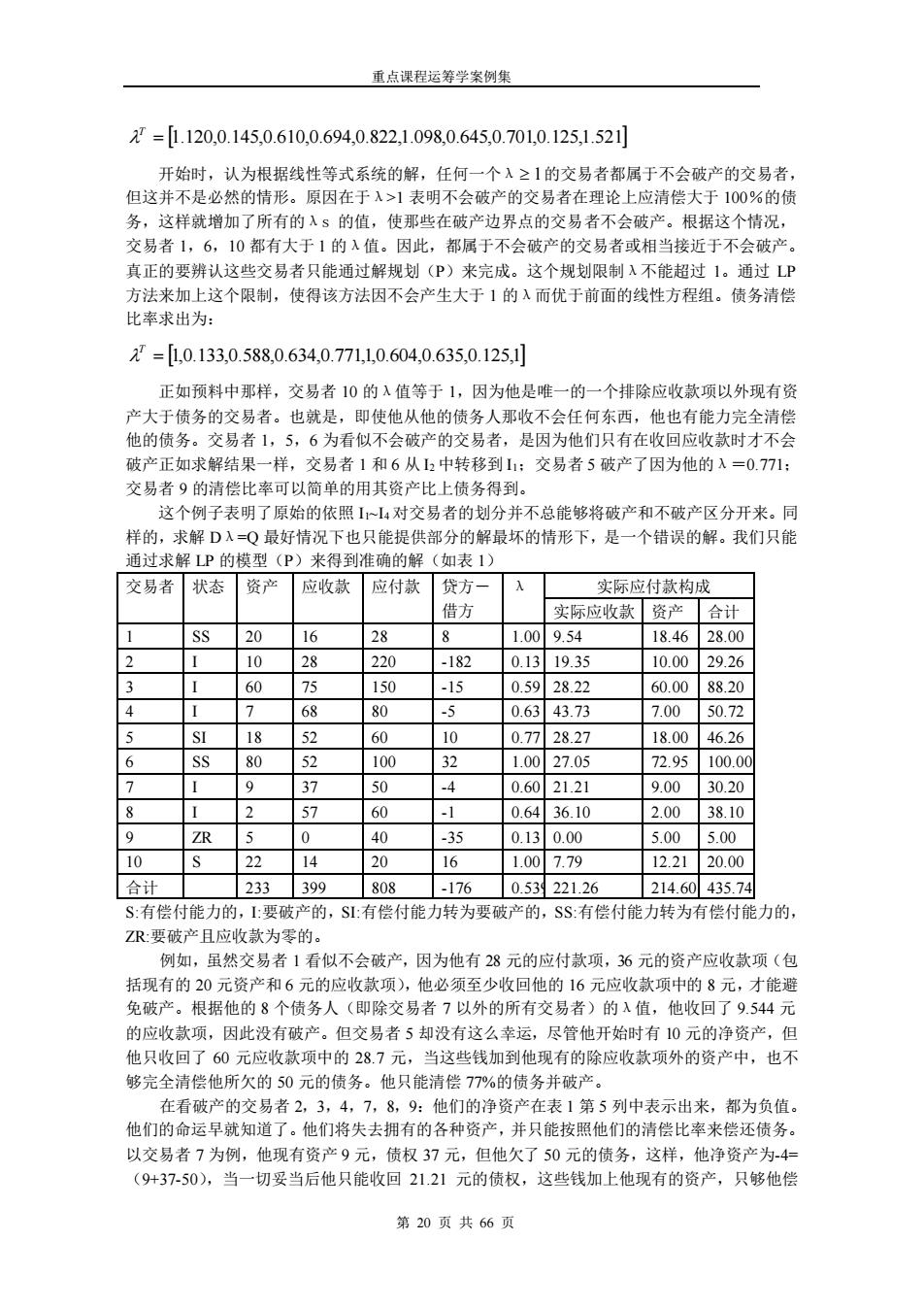
重点课程运筹学案例集 2'=[1.120,0.145.0.610.0.694,0.822,1.098,0.645,0.701,0.125,1.521 开始时,认为根据线性等式系统的解,任何一个入21的交易者都属于不会破产的交易者 但这并不是必然的情形。原因在于入>1表明不会破产的交易者在理论上应清偿大于100%的债 务,这样就增加了所有的入5的值,使那些在破产边界点的交易者不会破产。根据这个情况, 交易者1,6,10都有大于1的入值。因此,都属于不会破产的交易者或相当接近于不会破产。 真正的要辨认这些交易者只能通过解规划(P)来完成。这个规划限制λ不能超过1。通过LP 方法来加 上这个限制,使得该方法因不会产生大于1的入而优于前面的线性方程组。债务清偿 比率求出为 2=[0.133,0.588.0.6340.77110.604,0.635.0.125,1 正加预料中那样,交易者10的入值等于1,因为他是难一的一个排除应收款项以外现有济 产大于债务的交易者。也就是,即使他从他的债务人那收不会任何东西,他也有能力完全清 他的债务。交易者1,5,6为看似不会破产的交易者,是因为他们只有在收回应收款时才不会 破产正如求解结果一样,交易者1和6从中转移到【:交易者5破产了因为他的入=0771: 交易者9的清偿比率可以简单的用其资产比上债务得到。 这个例子表明了原始的依照1~4对交易者的划分并不总能够将破产和不破产区分开来。同 样的,求解D入=Q最好情况下也只能提供部分的解最坏的情形下,是一个错误的解。我们只能 通过求解LP的模型(P) 来得到准确的解 (如表1 交易者 状态资产 应收款应付款 贷方 实际应付款构成 借方 实际应收款资产合计 SS 20 8 8 100954 18462800 10 220 -182 0.1 19.35 10.0029.26 60 75 150 -15 0.5928.22 60.0088.20 7 68 80 .5 0.6343.73 7.0050.72 57 60 10 0.772827 18.0046.26 SS 80 52 100 32 1.00 27.0 72.95100.0 7 I 9 37 50 -4 0.602121 90030.20 57 60 .1 0643610 2003810 40 013 .00 5.005.00 10 22 14 20 16 1.007.79 12.2120.00 合计 233399808 -176 0.53221.26 214.60435.74 S:有偿付能力的,1要破产的,S1有偿付能力转为要破产的,SS:有偿付能力转为有偿付能力的, ZR要破产且应收款为零的。 创如, 虽然交易者1看似不会破产,因为他有28 元的应付款项,36元的资产应收款项(包 括现有的20元资产和6元的应收煮项),他必须至少收回他的16元应收款项中的8元,才能避 免破产。根据他的8个债务人(即除交易者7以外的所有交易者)的入值,他收回了9.544元 的应收款项,因此没有破产。但交易者5却没有这么幸运,尽管他开始时有10元的净资产,但 他只收回了60元应收款项中的287元,当这些钱加到他现有的除应收款项外的资产中,也不 够完全清偿他所欠的50元的债务。他只能清偿77%的债务并破产 在看破产的交易者2,3,4,7,8,9:他们的净资产在表1第5列中表示出来,都为负值 他们的命运早就知道了。他们将失去拥有的各种资产,并只能按照他们的清偿比率来偿还债务。 以交易者7为例,他现有资产9元,债权37元,但他欠了50元的债务,这样,他净资产为-4 (9+3750),当一切妥当后他只能收回2121元的债权,这些钱加上他现有的资产,只够他偿 第20页共66页
重点课程运筹学案例集 第 20 页 共 66 页 = 1.120,0.145,0.610,0.694,0.822,1.098,0.645,0.701,0.125,1.521 T 开始时,认为根据线性等式系统的解,任何一个λ 1 的交易者都属于不会破产的交易者, 但这并不是必然的情形。原因在于λ>1 表明不会破产的交易者在理论上应清偿大于 100%的债 务,这样就增加了所有的λs 的值,使那些在破产边界点的交易者不会破产。根据这个情况, 交易者 1,6,10 都有大于 1 的λ值。因此,都属于不会破产的交易者或相当接近于不会破产。 真正的要辨认这些交易者只能通过解规划(P)来完成。这个规划限制λ不能超过 1。通过 LP 方法来加上这个限制,使得该方法因不会产生大于 1 的λ而优于前面的线性方程组。债务清偿 比率求出为: = 1,0.133,0.588,0.634,0.771,1,0.604,0.635,0.125,1 T 正如预料中那样,交易者 10 的λ值等于 1,因为他是唯一的一个排除应收款项以外现有资 产大于债务的交易者。也就是,即使他从他的债务人那收不会任何东西,他也有能力完全清偿 他的债务。交易者 1,5,6 为看似不会破产的交易者,是因为他们只有在收回应收款时才不会 破产正如求解结果一样,交易者 1 和 6 从 I2 中转移到 I1;交易者 5 破产了因为他的λ=0.771; 交易者 9 的清偿比率可以简单的用其资产比上债务得到。 这个例子表明了原始的依照 I1~I4 对交易者的划分并不总能够将破产和不破产区分开来。同 样的,求解 Dλ=Q 最好情况下也只能提供部分的解最坏的情形下,是一个错误的解。我们只能 通过求解 LP 的模型(P)来得到准确的解(如表 1) 交易者 状态 资产 应收款 应付款 贷方- 借方 λ 实际应付款构成 实际应收款 资产 合计 1 SS 20 16 28 8 1.00 9.54 18.46 28.00 2 I 10 28 220 -182 0.13 19.35 10.00 29.26 3 I 60 75 150 -15 0.59 28.22 60.00 88.20 4 I 7 68 80 -5 0.63 43.73 7.00 50.72 5 SI 18 52 60 10 0.77 28.27 18.00 46.26 6 SS 80 52 100 32 1.00 27.05 72.95 100.00 7 I 9 37 50 -4 0.60 21.21 9.00 30.20 8 I 2 57 60 -1 0.64 36.10 2.00 38.10 9 ZR 5 0 40 -35 0.13 0.00 5.00 5.00 10 S 22 14 20 16 1.00 7.79 12.21 20.00 合计 233 399 808 -176 0.539 221.26 214.60 435.74 S:有偿付能力的,I:要破产的,SI:有偿付能力转为要破产的,SS:有偿付能力转为有偿付能力的, ZR:要破产且应收款为零的。 例如,虽然交易者 1 看似不会破产,因为他有 28 元的应付款项,36 元的资产应收款项(包 括现有的 20 元资产和 6 元的应收款项),他必须至少收回他的 16 元应收款项中的 8 元,才能避 免破产。根据他的 8 个债务人(即除交易者 7 以外的所有交易者)的λ值,他收回了 9.544 元 的应收款项,因此没有破产。但交易者 5 却没有这么幸运,尽管他开始时有 10 元的净资产,但 他只收回了 60 元应收款项中的 28.7 元,当这些钱加到他现有的除应收款项外的资产中,也不 够完全清偿他所欠的 50 元的债务。他只能清偿 77%的债务并破产。 在看破产的交易者 2,3,4,7,8,9:他们的净资产在表 1 第 5 列中表示出来,都为负值。 他们的命运早就知道了。他们将失去拥有的各种资产,并只能按照他们的清偿比率来偿还债务。 以交易者 7 为例,他现有资产 9 元,债权 37 元,但他欠了 50 元的债务,这样,他净资产为-4= (9+37-50),当一切妥当后他只能收回 21.21 元的债权,这些钱加上他现有的资产,只够他偿