西安电子科技大学：《电动力学 Electrodynamics》课程教学资源（课件讲稿）第4章 电磁波的传播 wave propagation

电磁波的传播 Xidian University 实部分量为： E,A(cosa cosot+sin asin ot) E,=B(cos B cos ot+sin Bsin ot)(4,B为实数) (1)线偏振：a=B=0,E=AE:+BE, 实部分量 E:=Acos@t (Eox=A) E =Bcosoot (Eoy =B) E与x轴夹角日=g1B与t无关，因此在波动过程中的 A 大小变，而方向不变。 西安电子科技大学

西安电子科技大学 A,B为实数 E A t t x  cos cos  sin sin E B t t y  cos cos  sin  sin 实部分量为： （1）线偏振：     0 ， x y E Ae Be    0   实部分量        cos ( ) cos ( ) 0 0 E B t E B E A t E A y y x x   与 轴夹角 与 无关，因此在波动过程中的 大小变，而方向不变。 E  x A B tg 1   t 电磁波的传播

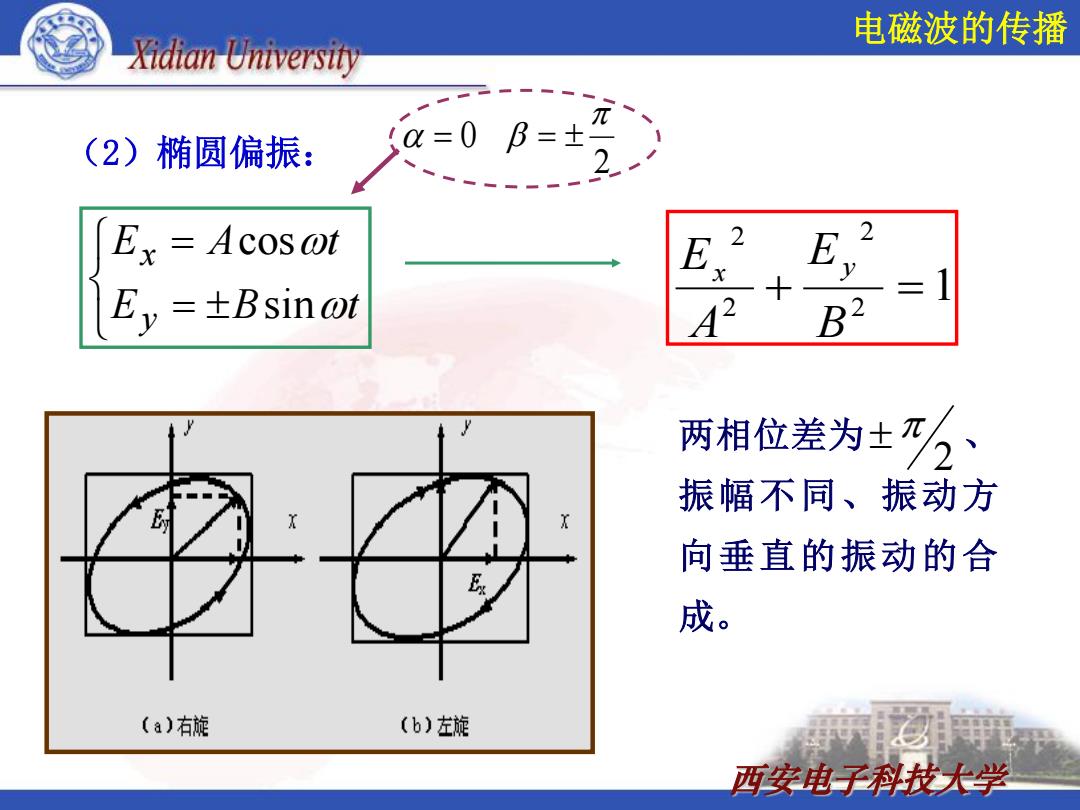
电磁波的传播 Xidian University π (2)椭圆偏振： (=0 B=± Ex=Acos@t 2 E 2 E 1 Ey=±Bsin@t B2 两相位差为±乃、 振幅不同、振动方 向垂直的振动的合 成。 (a)右旋 (b)左旋 西安电子科技大学

西安电子科技大学 （2）椭圆偏振：       E B t E A t y x   sin cos   0 2     1 2 2 2 2   B E A Ex y 两相位差为 、 振幅不同、振动方 向垂直的振动的合 成。 2   电磁波的传播

电磁波的传播 Xidian University 当A=B时，为圆偏振 0=g E,=士ggol=±ot 0=0t B 振动为右旋偏振（逆时针) 0=-0t 振动为左旋偏振（顺时针） 5.平面电磁波的能量和能流 >平面电磁波的能量密度 w= 6.D+i-2+ -B2 E 因为 =V= B w=E2 B2 电场能等于 L 磁场能 西安电子科技大学

西安电子科技大学 当 A  B 时，为圆偏振 1 1 y x E tg tg tg t t E             t        2      t  振动为左旋偏振（顺时针）        2   振动为右旋偏振（逆时针） 5．平面电磁波的能量和能流                 2 1 2 2 1 2 1 w E D H B E B        1  v  B E   2 2 B w  E  电场能等于 磁场能 平面电磁波的能量密度 因为 电磁波的传播

电磁波的传播 Xidian Universit >平面电磁波的能流密度 S=×i= 5-月E民×周应成=o 电磁能量传播方向与 电磁波传播方向一致 w=6E=6E0cos2(K-F-om）→ 2 S-veBe,-v6E cos(RF-) 计算公式 8=goe-ioti f= 5-ae×川=v fg =5f8oC0s 2☒ 西安电子科技大学

西安电子科技大学   2 S E H E e E E e k k             2 2 2 w E E k r t        0 cos   2 2 2 0 cos k k S v E e v E k r t e        2 0 2 1 w   E S E H  E n     2 0 2 1 Re 2 1       计算公式 0 0 1 cos 2 fg f g   i t f f e    0 it i g g e    0 平面电磁波的能流密度 电磁能量传播方向与   电磁波传播方向一致 1 k k k S E e E e v e           电磁波的传播

电磁波的传播 例：有一平面电磁波，其电场强度为 E(民，t)=100 rxexp[i(2π×10-2z-2π×106t)] (1)判断电场强度的方向和波传播的方向； (2)确定频率、波长和波速； (3) 若介质的磁导率4=4红x0' 求磁场强度； (4)求在单位时间内从一个与X一y平面平行的单位 面积通过的电磁场能量。 解：(1)E沿x轴方向振荡，元=亿，k=2π×102 波沿z方向传播。 (2)0=2元×106 f=”=106(E) 2元 λ= 2 =102(m) k v= =108( k 西安电子科技大学

西安电子科技大学 例：有一平面电磁波，其电场强度为  ,  100 exp[ (2 10 2 10 )] 2 6 E x t e i z t x             （1）判断电场强度的方向和波传播的方向； （2）确定频率、波长和波速； （3）若介质的磁导率 求磁场强度； （4）求在单位时间内从一个与 平面平行的单位 面积通过的电磁场能量。 4 10 ( ) 7 米      亨 x  y 波沿 方向传播。 解：（1） E 沿 轴方向振荡， ，  x k x kz   2 2 10 k    z ( ) 6 10 2 f   Hz   （2） 6   2 10 10 ( ) 2 2 m k     10 ( ) 8 s m k v    电磁波的传播