
■■■■■■ 图的存储表示 ■■■■■■■■■■■ 邻接矩阵(Adjacency Matrix)-- 数组表示法 ai 设图A=(N,E)是一个有n个顶点的图,图的邻接矩阵是 一个二维数组A.edge[nJ[n,定义: A.Edge [i]lj]= 若<i,j>eE或(i,j)∈E 0, 否则 Wij, 若i≠j且<i,j>eE或i,j)∈E A.Edge[i][门= dD 若i≠j且<i,j>廷E或i,j)E 0, 若i=j
图的存储表示 ◼ 设图 A = (V, E)是一个有 n 个顶点的图, 图的邻接矩阵是 一个二维数组 A.edge[n][n],定义: 邻接矩阵 (Adjacency Matrix) --数组表示法 = , , , ( , ) . [ ][ ] 否 则 若 或 0 1 < > A i j E i j E Edge i j = = = i j i j i , j i , j i j i , j i , j i j 若 若 且 或 若 且 或 , , ( ) , ( ) [ ][ ] 0 E E W E E A.Edge ij

0 0 A.Edge 0 0 0 A.Edge 10 0 0 。无向图的邻接矩阵是对称的; 。有向图的邻接矩阵可能是不对称的
◼ 无向图的邻接矩阵是对称的; ◼ 有向图的邻接矩阵可能是不对称的。 0 1 2 3 = 1 0 1 0 0 1 0 1 1 0 1 0 0 1 0 1 A.Edge 0 1 2 = 0 0 0 1 0 1 0 1 0 A.Edge
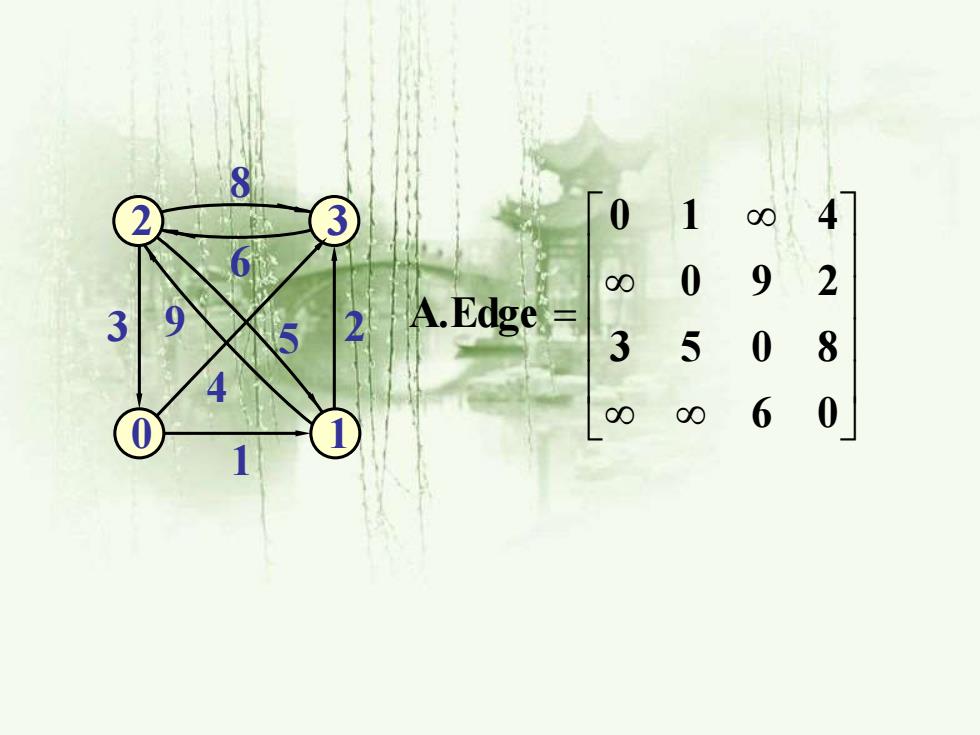
0 00 00 0 9 2 A.Edge= 3 5 0 8 00 6 0
86 3 1 9 2 5 4 20 31 = 6 0 3 5 0 8 0 9 2 0 1 4 A.Edge

有n个顶点的有向图需要n个存储单元来存储其 邻接矩阵:而无向图只需存入上(下)三角矩阵, 所以只需n(n+1)2个存储单元来存储其邻接矩 阵。 。在有向图中,统计第i行1的个数可得顶点i的出 度,统计第列1的个数可得顶点的入度。 在无向图中,统计第i行(列)1的个数可得顶点 的度
◼ 有n个顶点的有向图需要n 2个存储单元来存储其 邻接矩阵;而无向图只需存入上(下)三角矩阵, 所以只需n(n+1)/2个存储单元来存储其邻接矩 阵。 ◼ 在有向图中, 统计第 i 行 1 的个数可得顶点 i 的出 度,统计第 j 列 1 的个数可得顶点 j 的入度。 ◼ 在无向图中, 统计第 i 行 (列) 1 的个数可得顶点i 的度

优点:邻接矩阵比较容易判定图中任意两顶点之间是 否有边或弧,而且容易求得各个顶点的度数。 局限性:如果用邻接矩阵来检测图中共有多少条边或 弧,则必须按行按列对每个元素进行检测, 花费时间多
优点:邻接矩阵比较容易判定图中任意两顶点之间是 否有边或弧,而且容易求得各个顶点的度数。 局限性:如果用邻接矩阵来检测图中共有多少条边或 弧,则必须按行按列对每个元素进行检测, 花费时间多