0 ②
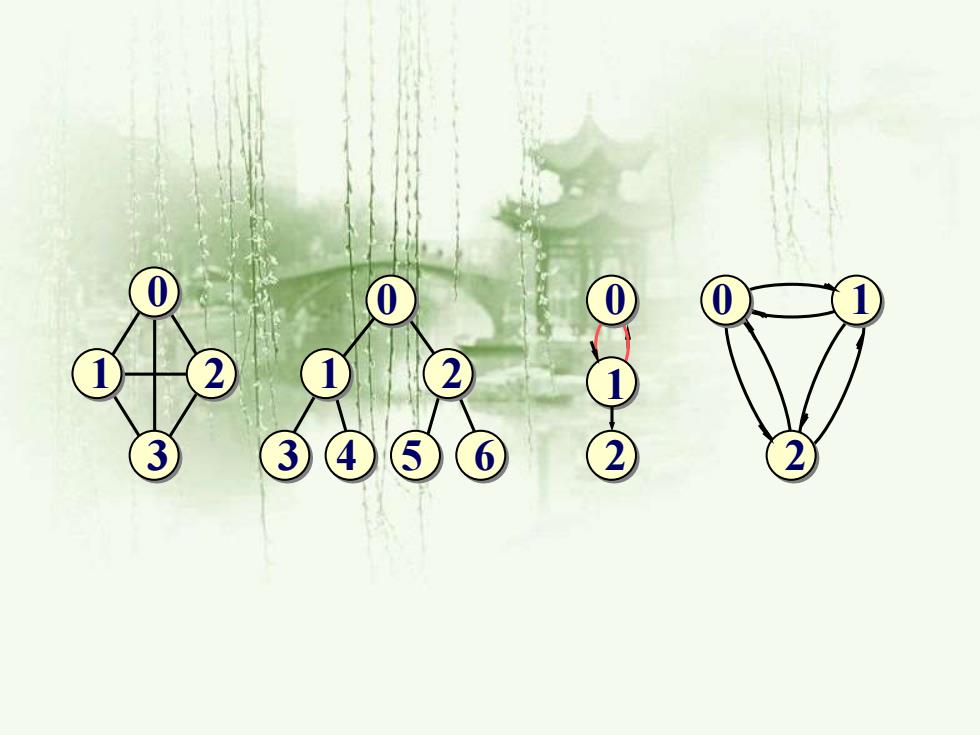
0 0 0 0 1 1 1 2 1 2 3 3 4 5 6 2 2
.子图设有两个图G=(V,目和G=(V, E)。若V∈V且EsE,则称图G'是图G 的子图。 子图 20 权图的边(或弧)具有与它相关的数,称 之为权。这种带权图叫做网(Network)
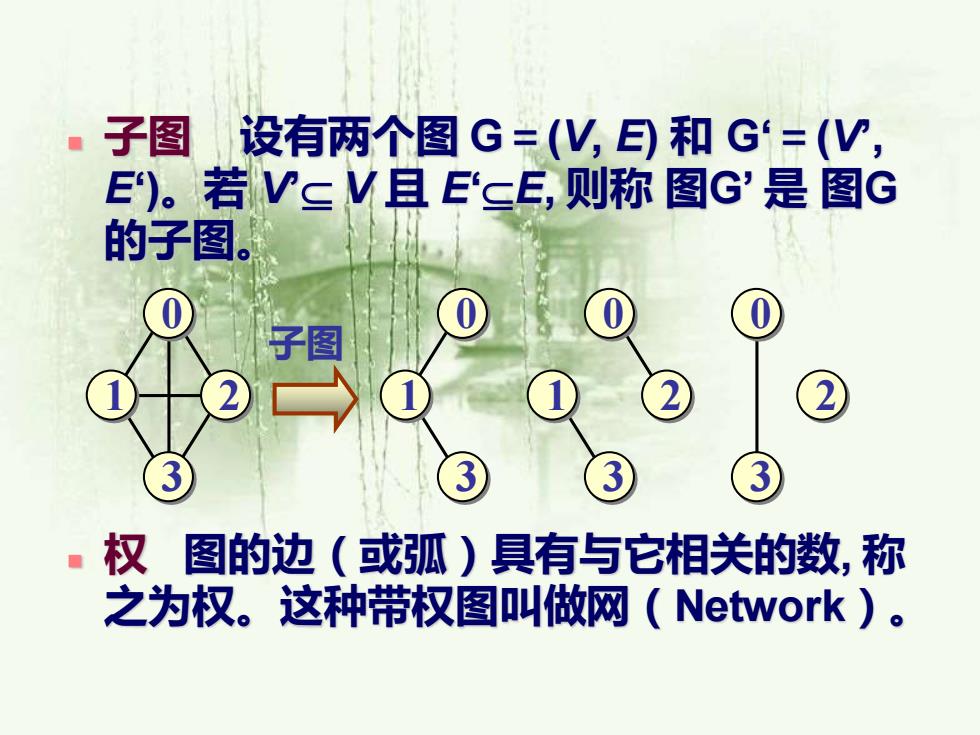
◼ 子图 设有两个图 G=(V, E) 和 G‘=(V’, E‘)。若 V’ V 且 E‘E, 则称 图G’ 是 图G 的子图。 ◼ 权 图的边(或弧)具有与它相关的数, 称 之为权。这种带权图叫做网(Network)。 0 1 2 3 子图 0 1 3 0 1 2 3 0 2 3

顶点的度一个顶点的度是与它相关联的边的条 数。记作TD()。在有向图中,顶点的度等于该顶 点的入度ID(W)与出度OD(W)之和。 以顶点v为始 以顶点v为终 点的有向边的 点的有向边的 条数 条数 路径在图G=(V,E中,若从顶点V,出发,沿一 些边经过一些顶点Vp,Vp2,,Vpm,到达顶点y 则称顶点序列(,V1Vp2…Vpmy)为从顶点v,到 顶点y的路径。它经过的边(VnVp1以(Vp1, Vp2小、(Vpmy)应是属于E的边
◼ 顶点的度 一个顶点v的度是与它相关联的边的条 数。记作TD(v)。在有向图中, 顶点的度等于该顶 点的入度ID(v)与出度OD(v)之和。 ◼ 路径 在图 G=(V, E) 中, 若从顶点 vi 出发, 沿一 些边经过一些顶点 vp1 , vp2 , …, vpm,到达顶点vj。 则称顶点序列 (vi vp1 vp2 ... vpm vj ) 为从顶点vi 到 顶点 vj 的路径。它经过的边(vi , vp1 )、(vp1 , vp2 )、...、(vpm, vj ) 应是属于E的边。 以 顶点v 为终 点的有向边的 条数 以 顶点v 为始 点的有向边的 条数

。路径长度非带权图的路径长度是指此路径上边 的条数。带权图的路径长度是指路径上各边的权 之和。 回路若路径上起始点和终止点重合,则称这样的 路径为回路或环
◼ 路径长度 非带权图的路径长度是指此路径上边 的条数。带权图的路径长度是指路径上各边的权 之和。 ◼ 回路 若路径上起始点和终止点重合, 则称这样的 路径为回路或环。 0 1 2 3 0 1 2 3 0 1 2 3

连通图与连通分量; 在无向图中,若从顶点V到 顶点V2有路径,则称顶点V与V2是连通的。如果 图中任意一对顶点都是连通的,则称此图是连通 图。非连通图的极大连通子图叫做连通分量。 强连通图与强连通分量在有向图中,若对于每 一对顶点V和y,都存在一条从v到y和从v到v的 路径,则称此图是强连通图。非强连通图的极大 强连通子图叫做强连通分量。 生成树一个连通图的生成树是其极小连通子图, 在n个顶点的情形下,有n-1条边
◼ 连通图与连通分量 在无向图中, 若从顶点v1到 顶点v2有路径, 则称顶点v1与v2是连通的。如果 图中任意一对顶点都是连通的, 则称此图是连通 图。非连通图的极大连通子图叫做连通分量。 ◼ 强连通图与强连通分量 在有向图中, 若对于每 一对顶点vi和vj , 都存在一条从vi到vj和从vj到vi的 路径, 则称此图是强连通图。非强连通图的极大 强连通子图叫做强连通分量。 ◼ 生成树 一个连通图的生成树是其极小连通子图, 在n个顶点的情形下,有n-1条边