
补充:推导过程!!!!! 振幅其大小是缓慢的单调下降,因此近似地有: 22 d.- 22 (A)k为奇数时,则 4-号+号-a+学-兮-a,+号)++ 2 4-9+号 22
振幅其大小是缓慢的单调下降,因此近似地有: 2 2 1 3 2 a a a = + 2 2 3 5 4 a a a = + 2 2 , −1 +1 = + k k k a a a 补充:推导过程!!!!! (A)k为奇数时,则 2 ) . 2 2 ) ( 2 2 ( 2 5 4 3 3 2 1 1 k k a a a a a a a a A = + − + + − + + + (1) 2 2 1 k k a a A = +

(B)k为偶数时,则 4=2+号-0+经-(号-a+2)+-号 (2) 22 综合(1)、(2)两式,有:
2 ) . 2 2 ) ( 2 2 ( 2 5 4 3 3 2 1 1 k k a a a a a a a a A = + − + + − + + − (2) 2 2 1 k k a a A = − 综合(1)、(2)两式,有: 2 ( 1) 2 1 k 1 k k a a A + = + − (B)k为偶数时,则

对自由空间传播的球面波,波面为无限大,k→o, ak→0,则对于给定轴线上的一点P的振幅为: A,=a 即球面波自由传播时,每各球面波上各次波 波源在P点产生的合振动等于第一个半波带在P点 产生的振动振幅的一半,强度为它的4分之1。 。=a
对自由空间传播的球面波,波面为无限大,k→, ak →0,则对于给定轴线上的一点P的振幅为: 2 1 1 A0 = a 即球面波自由传播时,每各球面波上各次波 波源在P点产生的合振动等于第一个半波带在P点 产生的振动振幅的一半,强度为它的4分之1。 2 4 1 1 0 I = a
三.矢量合成法 k为偶数 原则:从基线指向最末一矢量a终点,即为合 振动A的振动矢量
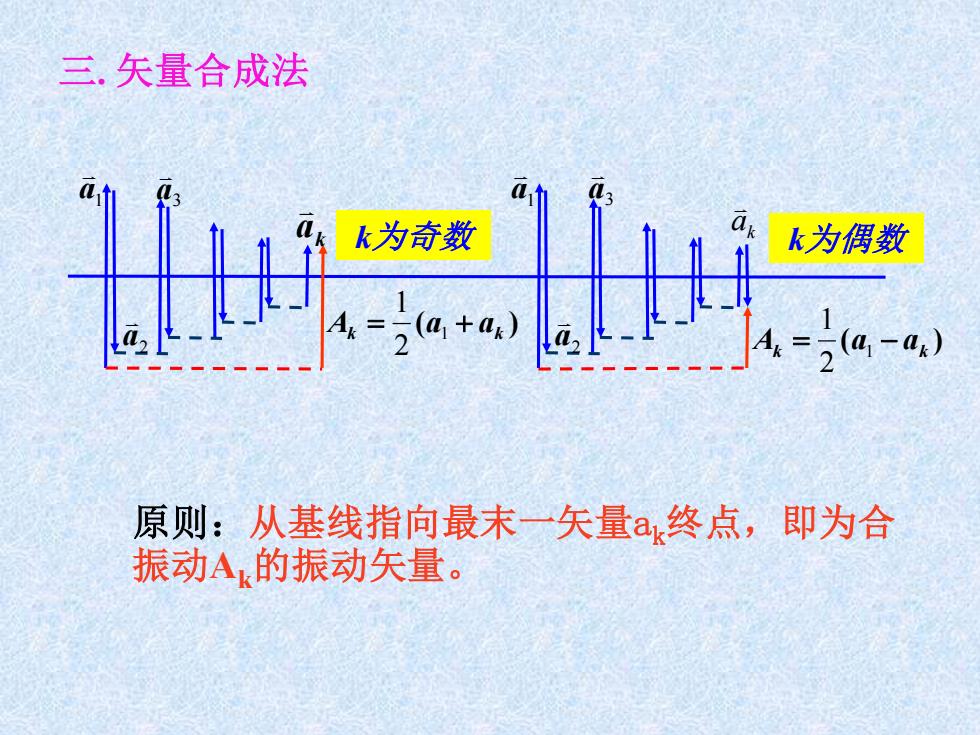
原则:从基线指向最末一矢量ak终点,即为合 振动Ak的振动矢量。 三. 矢量合成法 a3 2 a k a a1 a2 a3 a1 ( ) Ak = a1 + ak 2 1 k a ( ) Ak = a1 − ak 2 1 k为奇数 k为偶数

应该说,把波面分成半波带是不够精细的,特别 是当包含的不是整数半波带,在用半波带来处理 就因难了。 这时可以将半波带进一步细分,如将第一个半波带分 成个环带,则相邻半波带到P点的光程差为: 九 δ= 2m 相位差为: △0 π m 如果忽略倾斜因子的影响,则各个小波带在P 点产生的振幅A;近似相等
应该说,把波面分成半波带是不够精细的,特别 是当包含的不是整数半波带,在用半波带来处理 就困难了。 这时可以将半波带进一步细分,如将第一个半波带分 成m个环带,则相邻半波带到P点的光程差为: 2m = 相位差为: m = 如果忽略倾斜因子的影响,则各个小波带在P 点产生的振幅Ai 近似相等