
即 入 1-r0=3-1=3-3=.=1k-1-1= 2 这样分成的环形带叫做菲涅耳半波带,简称半波带。 6= p=π. 2 二、合振幅的计算 以a1、a2、a3、.分别表示各半波带发出的次波在P点 所产生的振幅。 由于相邻两个半波带所发出的次波到达P点时相位相差 π,所以k个半波带所发出的次波在P点叠加的合振幅A 为:
2 1 0 2 1 3 2 1 即 r −r = r − r = r − r == rk − rk− = 这样分成的环形带叫做菲涅耳半波带,简称半波带。 二、合振幅的计算 以a1、a2、a3、.分别表示各半波带发出的次波在P点 所产生的振幅。 由于相邻两个半波带所发出的次波到达P点时相位相差 ,所以k个半波带所发出的次波在P点叠加的合振幅Ak 为: 2 = =

A%=a1-a2+a-a4+a5++(-l)k+a 第k个半波带所发次波到达P点的振幅为: ax c Ko) Sk )Tk B (1)计算 R k 球冠的面积: ro S=2πR.R(1-c0Sp)=2πR(1-cosp)(1)
k k Ak a a a a a a 1 1 2 3 4 5 . ( 1) + = − + − + + + − 第k个半波带所发次波到达P点的振幅为: k k k r s a K k ( ) (1)计算 k k r S 球冠的面积: S = 2RR(1−cos) O R B0 Bk k Rh P k r l 0 r 2 (1 cos ) 2 = R − (1)
由图可得(余弦定理) R R2+(R+)2-r2 coso (2) 2R(R+6) 将(1)、(2)式分别微分得 ds=2πR2 sin do sin odo= rdr R(R+)
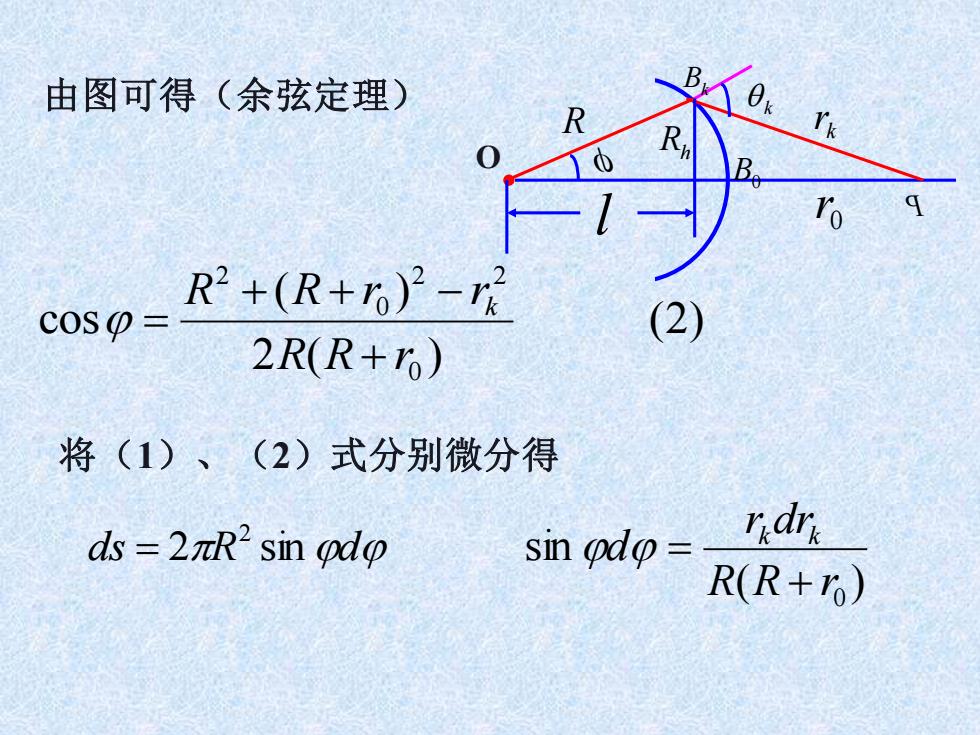
由图可得(余弦定理) O R B0 Bk k Rh P k r l 0 r (2) 2 ( ) ( ) cos 0 2 2 0 2 R R r R R r rk + + + − = 将(1)、(2)式分别微分得 ds 2R sin d 2 = ( ) sin 0 R R r r dr d k k + =

由上两式可得: ds 2uRdrg R+o 因为r>>入,故可将dr看着相邻半波带间r的差值 )/2,ds看着半波带的面积,于是有 πR Tk R+1 由此可见: ASk Ik 与k无关
由上两式可得: 0 2 R r Rdr r ds k k + = 因为rk>>,故可将drk看着相邻半波带间r的差值 /2,ds看着半波带的面积,于是有 0 R r R r S k k + = 由此可见: k k r S 与k无关

(2)倾斜因子K(0) 相邻的半波带之间,0变化甚微。 -g% 随着0k增大,缓慢减小 (3)综合考虑 Tk↑但△Skr.不变 k个 0个→K(0)减小 →1>a2>.> 所以: 奇正偶负
相邻的半波带之间,k变化甚微。 2 1 cos ( ) k k K + = (2)倾斜因子K(k ) 随着k增大,缓慢减小 (3)综合考虑 kh rkh 但sk /rk 不变 h gK ( ) 减小 a1 > a2 > . >ak ( ) 2 2 1 k k a a 所以: A p 奇正偶负