
③ ds dEp ④ P 2元A,A=m(相位差Ap,光程养d 求P点光振动E的数学表达式: dE()(p))ds r K()有性质:倾斜因子 0↑→K(8)↓:0↓→K(0)个 对于球面波或平面波,初相位可取为零,且倾斜因子: K(0)= 1+cos0 它可以解释子波为什么不会向后退. 2
ds ③ dEp ④ , ( ) 2 = = nr 相位差 ,光程差 求 P 点光振动 E 的数学表达式: cos( ) ( ) k r t r dsK dE − k r t ds r K dE p C cos( ) ( ) ( ) = − → ( ) → ( ) ( ) K K K θ ; 有性质: 对于球面波或平面波,初相位可取为零, 且倾斜因子: 2 1 cos K( ) + = 它可以解释子波为什么不会向后退. 倾斜因子

波面上有一定振幅分布,分布函数为A(⑨) .dE-C()K(0)cos(kr-@)ds 或:iE(p)=c4A(K(@)er-oy ds 菲涅耳衍射积分公式: pn-sn=ceI4eoes 或: E-c∬AOkO。+s 一般积分 较困难,故 分成两类
波面上有一定振幅分布,分布函数为 A(Q) A Q K k r t dS r dE C ( ) ( )cos( ) 1 = − ( ) ( ) dS r A Q K e dE p C i( k r t ) − ( ) = ( ) ( ) − = = S i t ikr S e dS r A Q K E p dE p Ce ( ) ( ) 菲涅耳衍射积分公式: 或: ( ) ( ) = S ikr e dS r A Q K E C ~ ~ 或: 一般积分 较困难,故 分成两类
三、衍射的分类 光源和考察点到障碍物的距离 1、菲涅耳衍射 光源 光源一障碍物一接收屏 距离为有限远(近场衍射) B 障碍物 接收屏 2、夫琅禾费衍射 光源 光源一障碍物一接收屏 S 距离为无限远(远场衍射) B 障碍物 接收屏
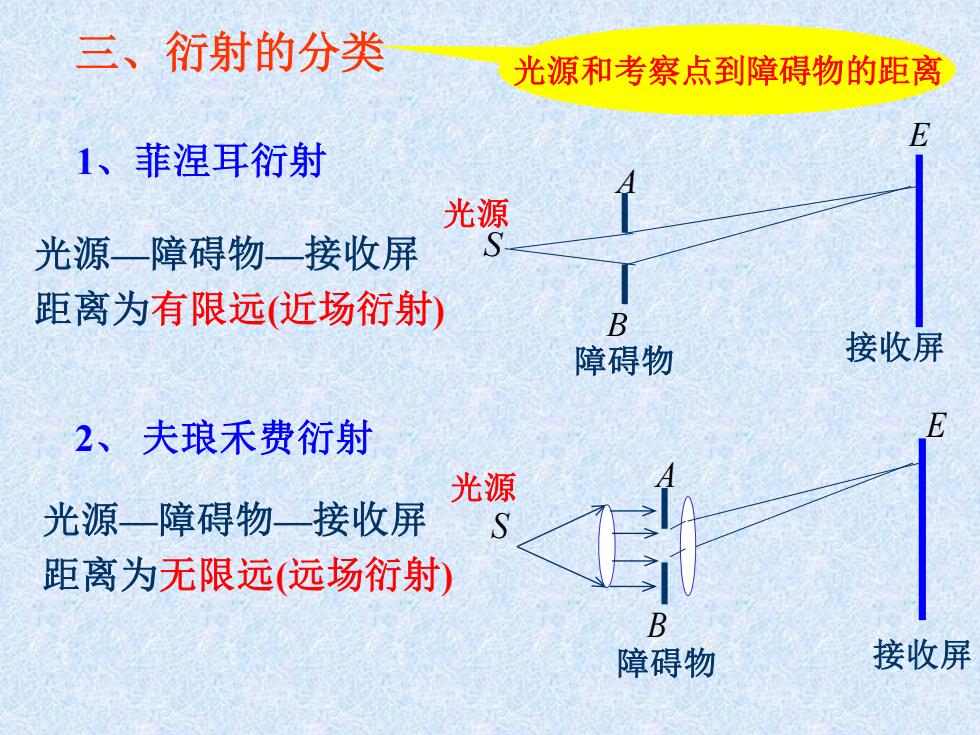
三、衍射的分类 光源和考察点到障碍物的距离 1、菲涅耳衍射 光源—障碍物—接收屏 距离为有限远(近场衍射) S A B E 光源 障碍物 接收屏 2、 夫琅禾费衍射 光源—障碍物—接收屏 距离为无限远(远场衍射) S A B E 光源 障碍物 接收屏

3、处理方法 (1)菲涅耳半波带法一近场衍射,对称的孔、阑 (2)菲涅耳积分法一远场衍射,单缝、直边、矩孔
3、处理方法 (1)菲涅耳半波带法—近场衍射,对称的孔、阑 (2)菲涅耳积分法—远场衍射,单缝、直边、矩孔
§2.3菲涅耳半波带 Fresnel Half-wave Zone) 一、菲涅耳半波带 现以点光源为例说明惠更斯一菲涅耳原理的应用。如图: O为点光源,S为任一时刻的波面,R为半径。 令PBo=ro? 设想将波面分为许多环形带,使从每两个相邻带的相应边缘 到P点的距离相差半个波长
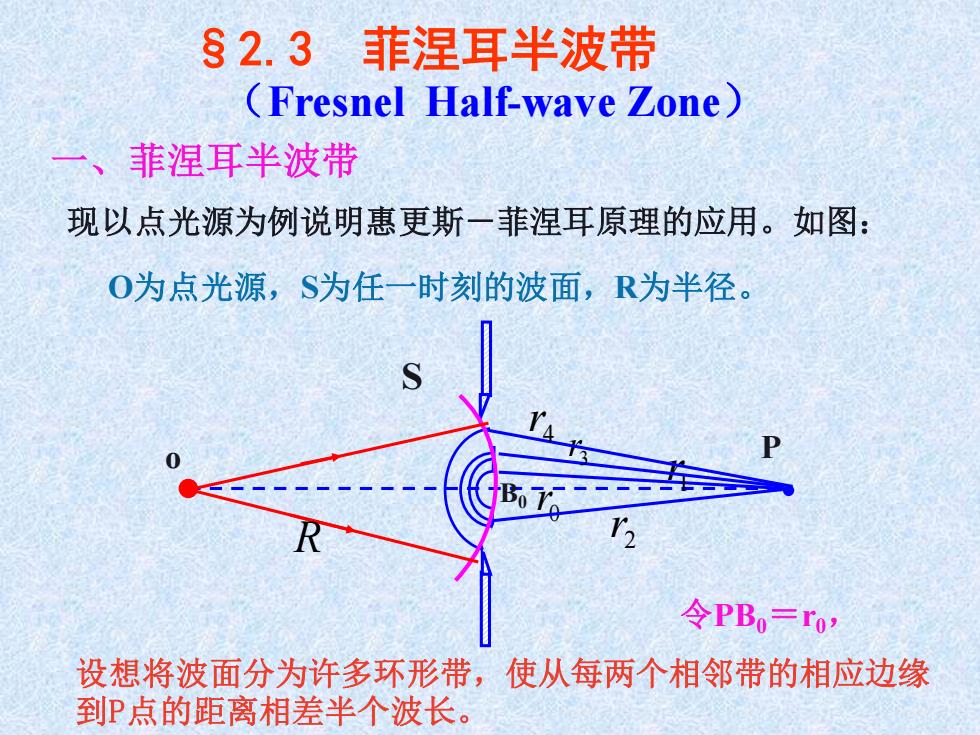
§2.3 菲涅耳半波带 (Fresnel Half-wave Zone) 一、菲涅耳半波带 现以点光源为例说明惠更斯-菲涅耳原理的应用。如图: P 0 r 1 r 2 r 3 r 4 r o O为点光源,S为任一时刻的波面,R为半径。 B0 令PB0=r0, 设想将波面分为许多环形带,使从每两个相邻带的相应边缘 到P点的距离相差半个波长。 S R