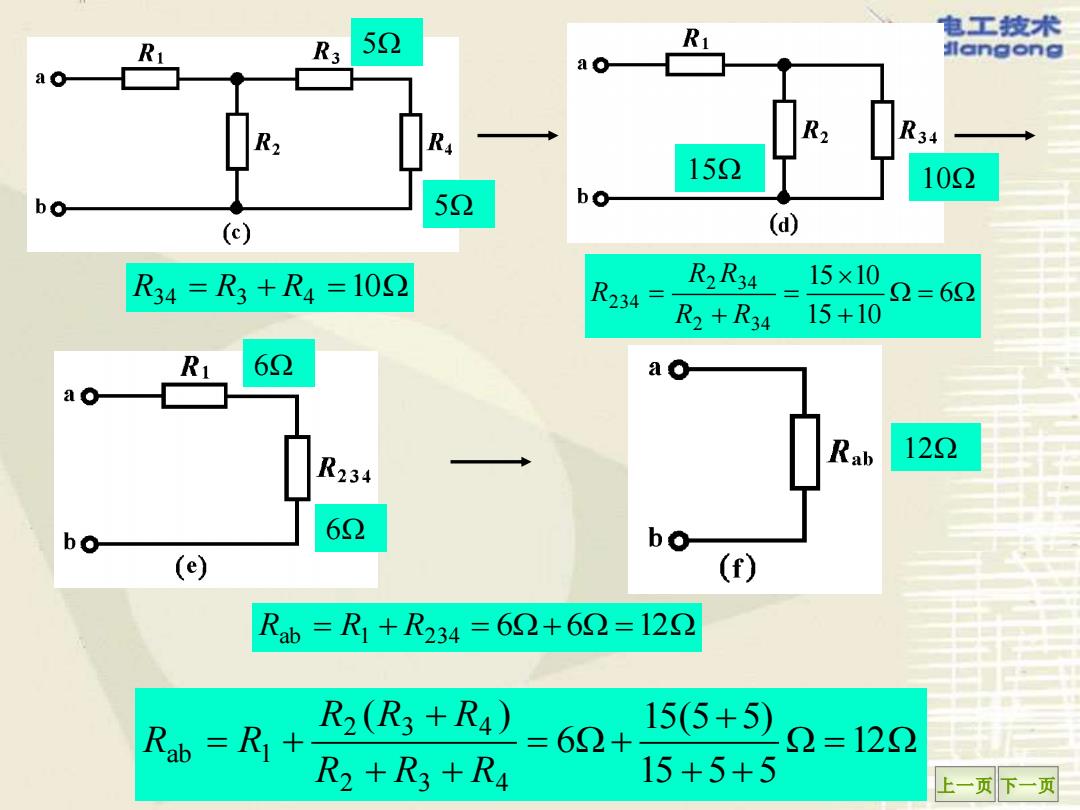
电工技术 5 dlangong a● 34 152 102 bo 52 bo (c) (d) R34=R3+R4=102 R2R34 15×10 R234 2=62 R2+R3415+10 R 62 a● ao Rab 122 R234 62 bo bo (e) (f) Rab=R1+R234=62+62=122 R2(R3+R4) =62+ 15(5+5) Q=122 R2+R3+R4 15+5+5 上一页下一页
上一页 下一页 5 5 15 10 6 6 12 R34 = R3 + R4 =10 = + = + = 6 15 10 15 10 2 34 2 34 234 R R R R R Rab = R1 + R234 = 6+ 6 =12 = + + + = + + + + = + 12 15 5 5 15(5 5) 6 ( ) 2 3 4 2 3 4 ab 1 R R R R R R R R
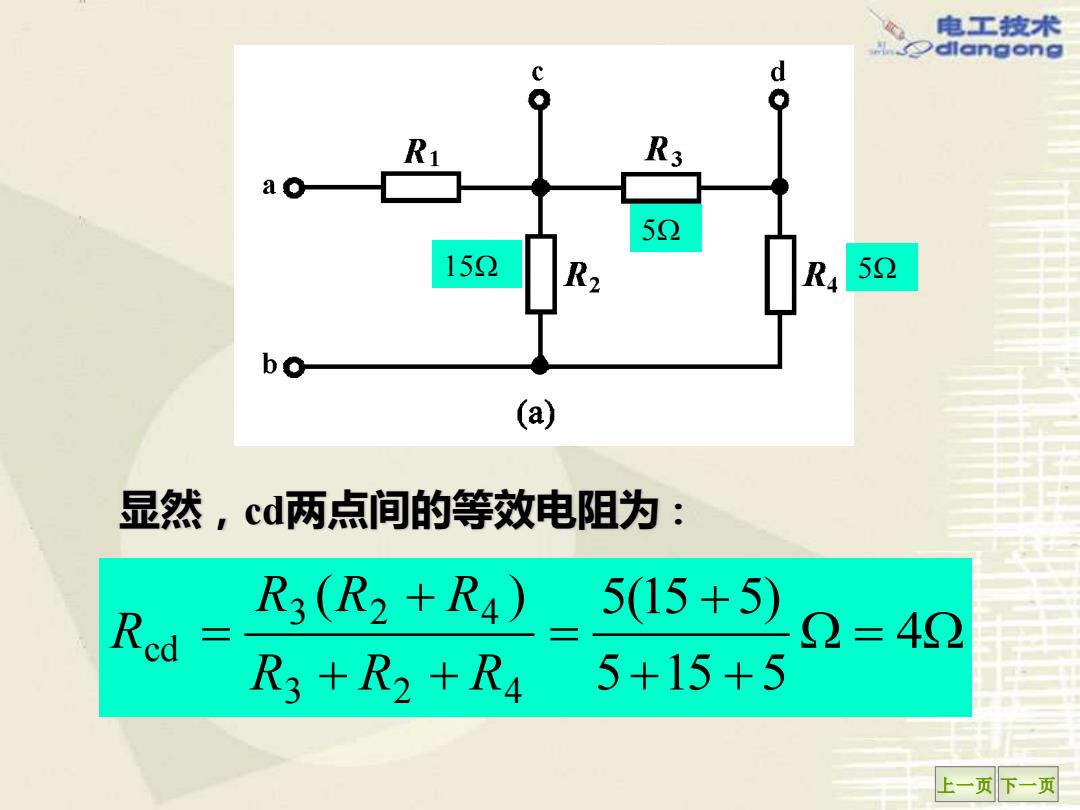
电工技术 dlangong c d R3 ao 52 152 R2 52 bo (a) 显然,cd两点间的等效电阻为: R3(R2+R4) Rcd= 5(15+5) 2=42 R3+R2+R4 5+15+5 上一页下一页
上一页 下一页 显然,cd两点间的等效电阻为: = + + + = + + + = 4 5 15 5 ( ) 5(15 5) 3 2 4 3 2 4 cd R R R R R R R 15 5 5

上一页 下一页

电工技术 dlangong 2.2电阻星形联结与三角形联结的等换 ⊙0◇◇0⊙⊙0⊙00⊙◇00◆0◇00⊙0◇0@0◇000◇@0@◇0@◇◇0◇00⊙◇ 本节的要求:本节为选讲,主要讲授 电阻星形联结与三角形 联结的等效变换公式 上一页下一页
上一页 下一页 2.2 电阻星形联结与三角形联结的等换 本节的要求:本节为选讲,主要讲授 电阻星形联结与三角形 联结的等效变换公式
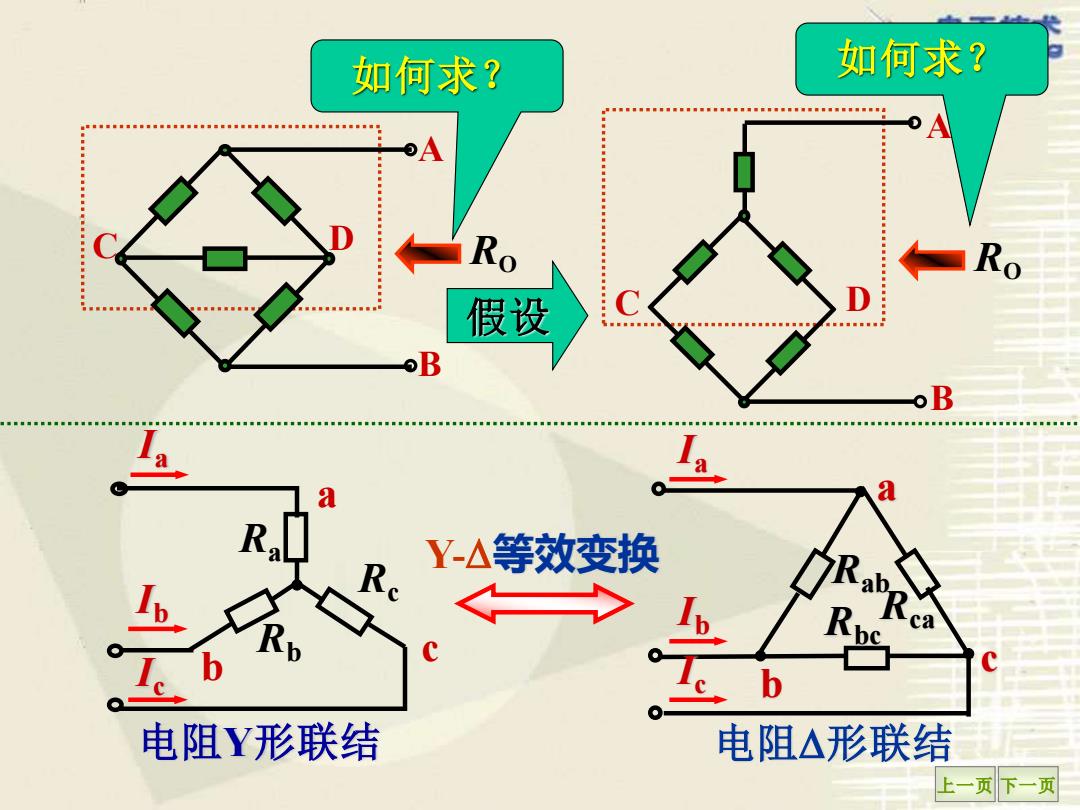
如何求? 如何求? Ro 假设 B Y-△等效变换 电阻Y形联结 电阻△形联结 上一页下一页
上一页 下一页 RO 电阻形联结 Y-等效变换 电阻Y形联结 RO C B A D C A D B Ia Ib Ic b c Ra Rc Rb a a c b R Rca bc Rab Ia Ib Ic 如何求? 如何求? 假设