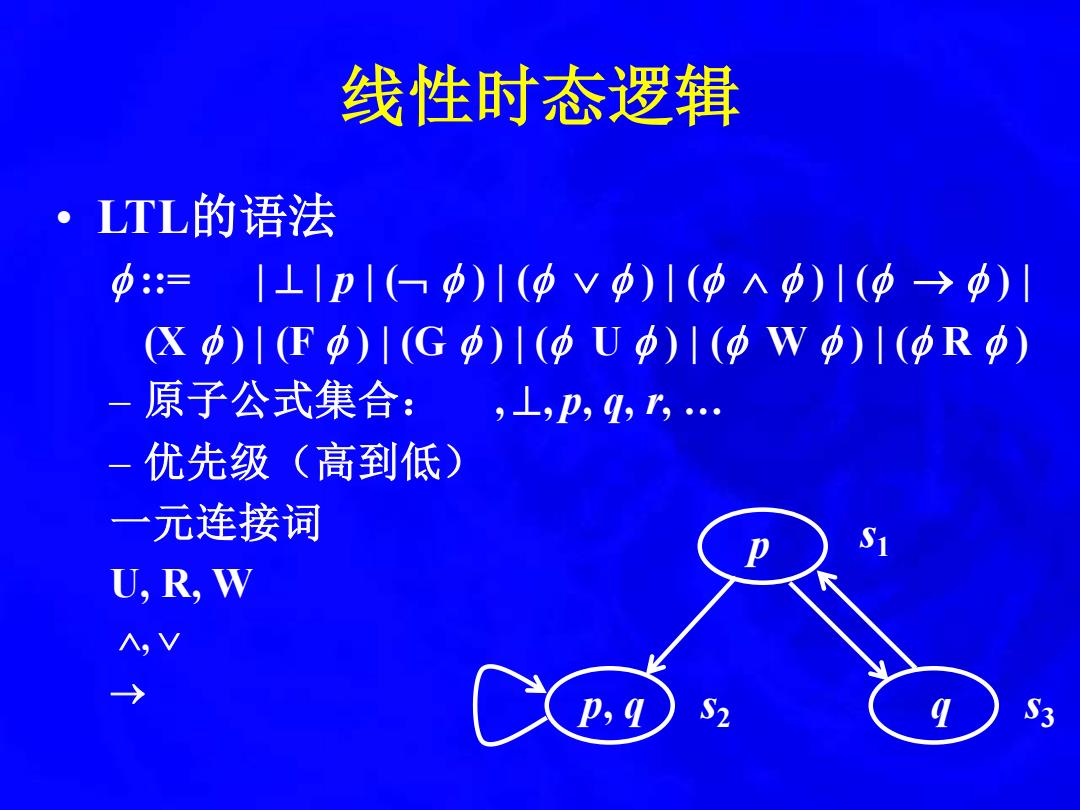
线性时态逻辑 ·LTL的语法 中:= 1⊥1p|(φ)1(φvφ)1(中Λφ)1(φ→p) ☒φ)I(Fφ)1(Gφ)1(φUφ)I(φWφ)|(φRφ) -原子公式集合: ,⊥,p,q,r,… -优先级(高到低) 一元连接词 U,R,W S3
线性时态逻辑 • LTL的语法 ::= | ⊥ | p | ( ) | ( ) | ( ) | ( → ) | (X ) | (F ) | (G ) | ( U ) | ( W ) | ( R ) – 原子公式集合: , ⊥, p, q, r, … – 优先级(高到低) 一元连接词 U, R, W , → p p, q q s1 s3 s2

线性时态逻辑 ·LTL的语义模型 -是一个Kripke结构 (S,S,→,A,L) 即状态迁移系统:状态集合S,开始状态So,迁 移关系→,标记集合A,标记函数L -其中对迁移关系的要求:VsS.3s'S.s→s 一通常用状态迁移图表示 -以后的讨论用简化的三元组(S,→,L〉 模型的路径 状态迁移的无限序列元=S1→S2→… -π表示从S,开始的后缀S→S+1→·
线性时态逻辑 • LTL的语义模型 – 是一个Kripke结构(S, s0 , →, A, L) – 即状态迁移系统:状态集合S,开始状态s0,迁 移关系→,标记集合A,标记函数L – 其中对迁移关系的要求:s:S. s':S. s → s' – 通常用状态迁移图表示 – 以后的讨论用简化的三元组(S, →, L) • 模型 的路径 – 状态迁移的无限序列 = s1 → s2 → … – i 表示从si 开始的后缀 si → si+1 → …

线性时态逻辑 。模型 上路径π的满足关系 元 ⊥,元pfp∈L(),元中fπ 一元 功入中f元 4且元 一元 中v功f元 中或π必 一元 中→办fπ4蕴涵元4 一元 X中fπ2中 一 元 G功f对所有的i≥1,有π 一 元 F中f存在某个i≥1,使得π 元 φUΨf存在某个i≥1,使得π w,且对 所右的;=1 1右m引 人
线性时态逻辑 • 模型 上路径的满足关系 – , ⊥, p iff p L(s1 ), iff – 1 2 iff 1 且 2 – 1 2 iff 1 或 2 – 1 → 2 iff 1 蕴涵 2 – X iff 2 – G iff 对所有的i 1,有 i – F iff 存在某个i 1,使得 i – U iff 存在某个i 1,使得 i ,且对 所有的j =1, …, i −1有 j

线性时态逻辑 ·模型 上路径π的满足关系 Uwf存在某个i≥1,使得πy,且对 所有的j1,,i-1有元功 S1→S2→S3→S4→S5→S6→S7→S8→S9S10→… π(3≤i≤9)满足pUq
线性时态逻辑 • 模型 上路径的满足关系 – U iff 存在某个i 1,使得 i ,且对 所有的j =1, …, i −1有 j s1 → s2 → s3 → s4 → s5 → s6→ s7→ s8→ s9→s10→ … i ( 3 i 9)满足p U q p q

线性时态逻辑 ·模型 上路径π的满足关系 pUwf存在某个i≥1,使得πw,且对 所有的j=1,,i-1有元功 一元 pWΨf存在某个i≥1,使得π w,且 对所有的i=1,,i-1有 中;或者对所有的飞 ≥1有πk 中R业f存在某个i≥1,使得π中,且对 所有的j=1,,i有w;或者对所有的k≥1有 元k
线性时态逻辑 • 模型 上路径的满足关系 – U iff 存在某个i 1,使得 i ,且对 所有的j =1, …, i −1有 j – W iff 存在某个i 1,使得 i ,且 对所有的j =1, …, i −1有 j ;或者对所有的k 1有 k – R iff 存在某个i 1,使得 i ,且对 所有的j =1, …, i 有 j ;或者对所有的k 1有 k