
模型检测及所用逻辑概述 基于时态逻辑的模型检测 模型是一个状态迁移系统 -性质·是时态逻辑的公式,在某些状态下为真, 在其它状态下为假(公式的真与假不是静态的) 验证系统 满足性质φ 一用模型检测器的描述语言建立系统的模型 用模型检测器的规范语言对待证性质进行编码, 得到时态逻辑公式中 -以 和作为输入,运行模型检测器 若 中,则产生由系统执行轨迹构成的反例
模型检测及所用逻辑概述 • 基于时态逻辑的模型检测 – 模型 是一个状态迁移系统 – 性质 是时态逻辑的公式,在某些状态下为真, 在其它状态下为假(公式的真与假不是静态的) • 验证系统 满足性质 – 用模型检测器的描述语言建立系统的模型 – 用模型检测器的规范语言对待证性质进行编码, 得到时态逻辑公式 – 以 和作为输入,运行模型检测器 – 若 ,则产生由系统执行轨迹构成的反例

模型检测及所用逻辑概述 时态逻辑是一个庞大的家族 归类到模态逻辑,依赖于对“时间”的特别观点 进行内部分类 -线性时态逻辑: 时间是线性的逻辑 一计算树逻辑:时间形成分支的逻辑 常用于硬件和通信协议的验证中 -现在开始用于软件的验证
模型检测及所用逻辑概述 • 时态逻辑是一个庞大的家族 归类到模态逻辑,依赖于对“时间”的特别观点 进行内部分类 – 线性时态逻辑:时间是线性的逻辑 – 计算树逻辑:时间形成分支的逻辑 – 常用于硬件和通信协议的验证中 – 现在开始用于软件的验证
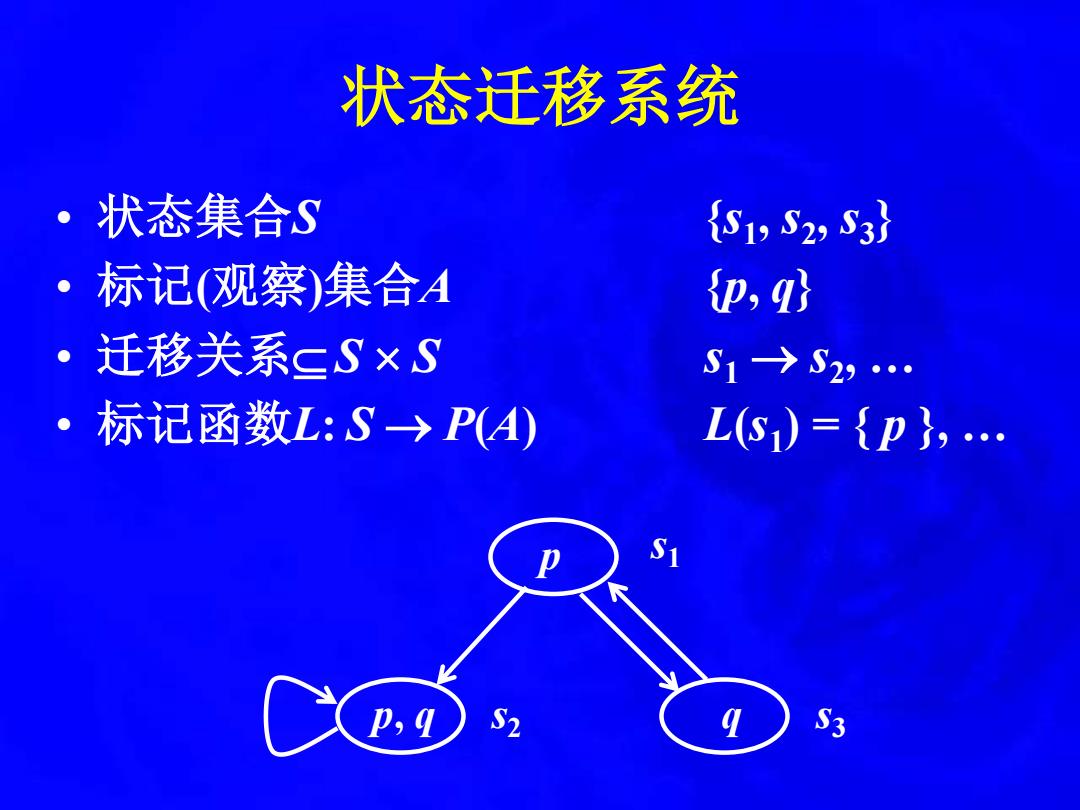
状态迁移系统 ·状态集合S {S1,S2,S3} ·标记(观察)集合A p,g 迁移关系sS×S S1→S23… 。1 标记函数L:S→PA) L(S)={p},… P,q S2 S3
状态迁移系统 • 状态集合S {s1 , s2 , s3 } • 标记(观察)集合A {p, q} • 迁移关系 S S s1 → s2 , … • 标记函数L: S → P(A) L(s1 ) = { p }, … p p, q q s1 s3 s2
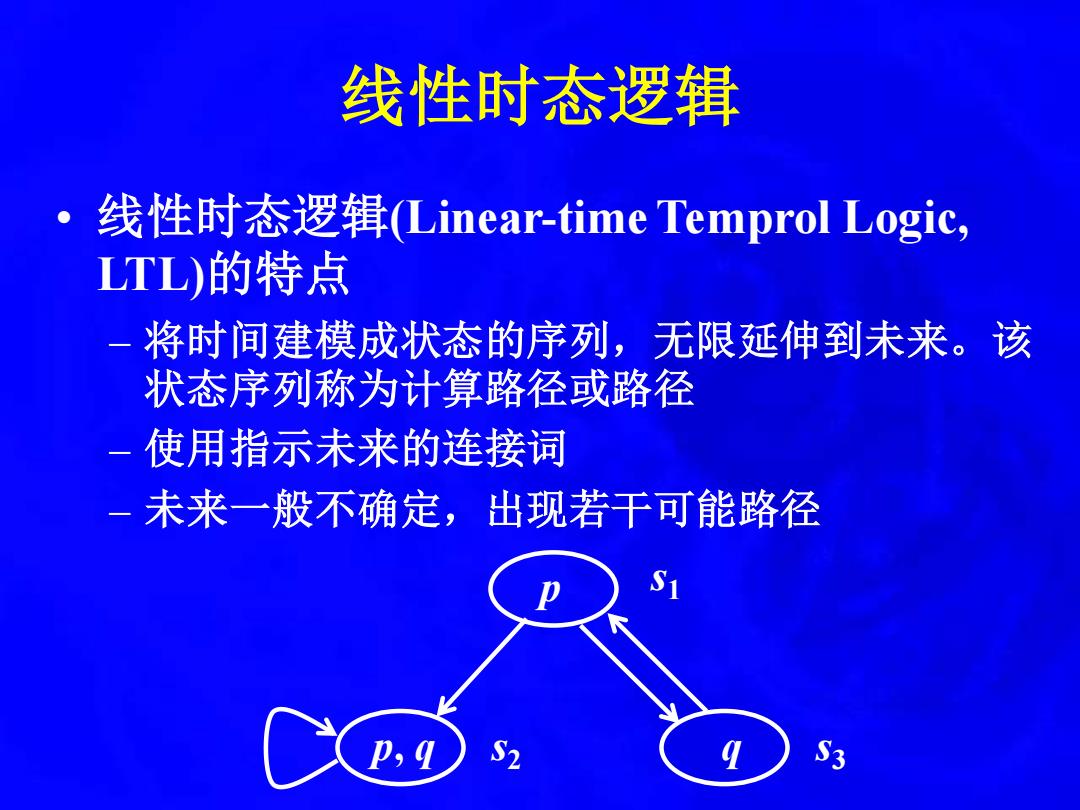
线性时态逻辑 线性时态逻辑(Linear-time Temprol Logic, LTL)的特点 将时间建模成状态的序列,无限延伸到未来。该 状态序列称为计算路径或路径 -使用指示未来的连接词 一未来一般不确定,出现若干可能路径 S2 S3
线性时态逻辑 • 线性时态逻辑(Linear-time Temprol Logic, LTL)的特点 – 将时间建模成状态的序列,无限延伸到未来。该 状态序列称为计算路径或路径 – 使用指示未来的连接词 – 未来一般不确定,出现若干可能路径 p p, q q s1 s3 s2
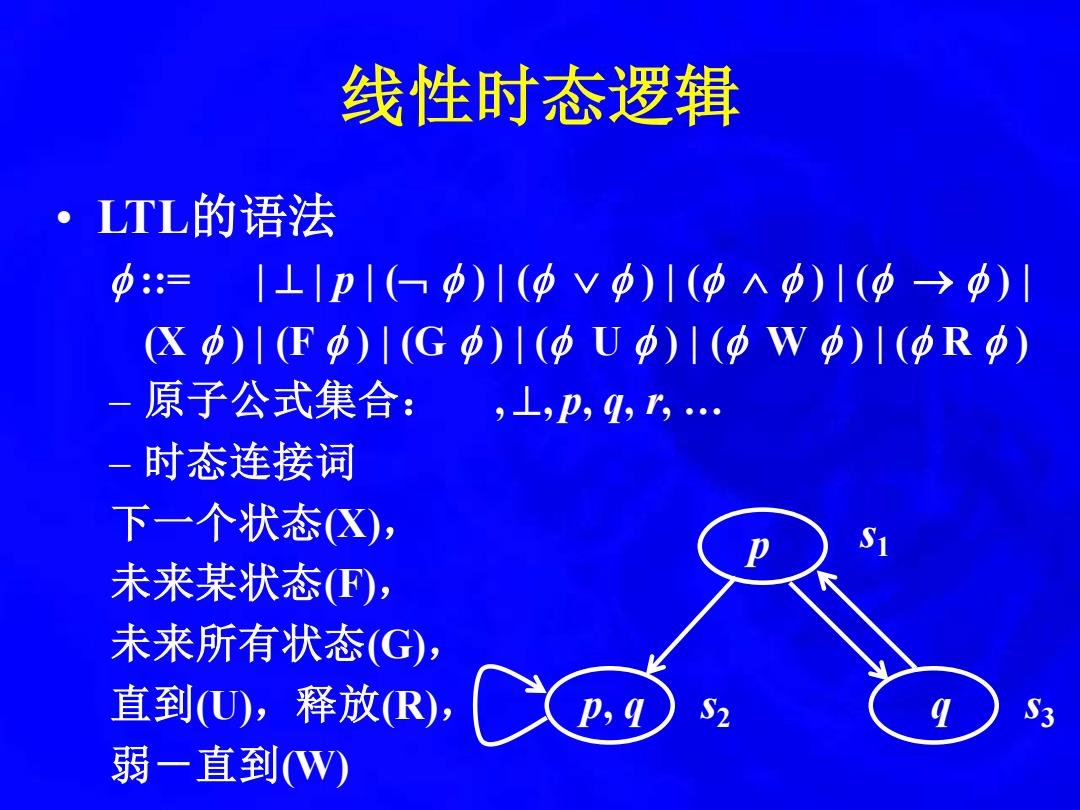
线性时态逻辑 ·LTL的语法 功:= 1⊥|p1(φ)|(φvp)1(φΛφ)1(φ>中)1 ☒φ)1Fφ)1(Gφ)1(φUφ)I(φWφ)1(φRφ) 一原子公式集合: ,⊥L,p,q3… 一时态连接词 下一个状态X), 未来某状态F), 未来所有状态(G), 直到U),释放R), S3 弱一直到W)
线性时态逻辑 • LTL的语法 ::= | ⊥ | p | ( ) | ( ) | ( ) | ( → ) | (X ) | (F ) | (G ) | ( U ) | ( W ) | ( R ) – 原子公式集合: , ⊥, p, q, r, … – 时态连接词 下一个状态(X), 未来某状态(F), 未来所有状态(G), 直到(U),释放(R), 弱-直到(W) p p, q q s1 s3 s2