
线性时态逻辑 ·Rw等价于(一U一w 一功Uwf存在某个i≥1,使得π ,且对所有的i=1,,i-1有一中 S1→S2→,→S1→S→S+1→. 一 pRwf存在某个i≥1,使得π中,且对 所有的i=1,,i有πy; 或者对所有的k≥1有 元 Ψ(两种情况) S1→S2→…>S-1→S→St1→…
线性时态逻辑 • R 等价于( U ) – U iff 存在某个i 1,使得 i ,且对所有的j =1, …, i −1有 j s1 → s2 → … → si-1 → si → si+1→ … – R iff 存在某个i 1,使得 i ,且对 所有的j =1, …, i 有 j ;或者对所有的k 1有 k (两种情况) s1 → s2 → … → si-1 → si → si+1→ …

线性时态逻辑 ·Rw等价于(U一w) 一pUwf存在某个i≥1,使得π ,且对所有的i=1,,i-1有一中 S1→S2→,→S1→S→S+1→. 一 pRwf存在某个i≥1,使得π中,且对 所有的i=1,,i有y; 或者对所有的k≥1有 πkΨ(其中较简单的情况) S1>S2今…→S-1→S:→S+1→…
线性时态逻辑 • R 等价于( U ) – U iff 存在某个i 1,使得 i ,且对所有的j =1, …, i −1有 j s1 → s2 → … → si-1 → si → si+1→ … – R iff 存在某个i 1,使得 i ,且对 所有的j =1, …, i 有 j ;或者对所有的k 1有 k (其中较简单的情况) s1 → s2 → … → si-1 → si → si+1→ …

线性时态逻辑 ·中Rw等价于(U一) 一功Uwf存在某个i≥1,使得π ,且对所有的i=1,,i-1有一中 S1→S2→,→S1→S→S+1→. 一 pRwf存在某个i≥1,使得π中,且对 所有的j=1,,i有πy;或者对所有的k≥1有 (其中较复杂的情况)中 S1→S2→…→S-1-→S→St1→…
线性时态逻辑 • R 等价于( U ) – U iff 存在某个i 1,使得 i ,且对所有的j =1, …, i −1有 j s1 → s2 → … → si-1 → si → si+1→ … – R iff 存在某个i 1,使得 i ,且对 所有的j =1, …, i 有 j ;或者对所有的k 1有 k (其中较复杂的情况) s1 → s2 → … → si-1 → si → si+1→ …

线性时态逻辑 ·Ry等价于-(一U一の 一中Uwf存在某个i≥1, 使得π ,且对所有的i=1,,i-1有π W S1→S2→.→S1→S→SH1→ 一元 中RΨf存在某个i≥1,使得π,且对 所有的i=1,,i有πw; 或者对所有的k≥1有 元k ”其中较复杂的情祝 S1今S2〉…→S1→S→S+1→
线性时态逻辑 • R 等价于( U ) – U iff 存在某个i 1,使得 i ,且对所有的j =1, …, i −1有 j s1 → s2 → … → si-1 → si → si+1→ … – R iff 存在某个i 1,使得 i ,且对 所有的j =1, …, i 有 j ;或者对所有的k 1有 k (其中较复杂的情况) s1 → s2 → … → si-1 → si → si+1→ …
线性时态逻辑 中(简记s中) 若对每条开始于s的路径π都有π 例 So Xr P,q X(4Λr) G(p∧r) 9,1 Gr
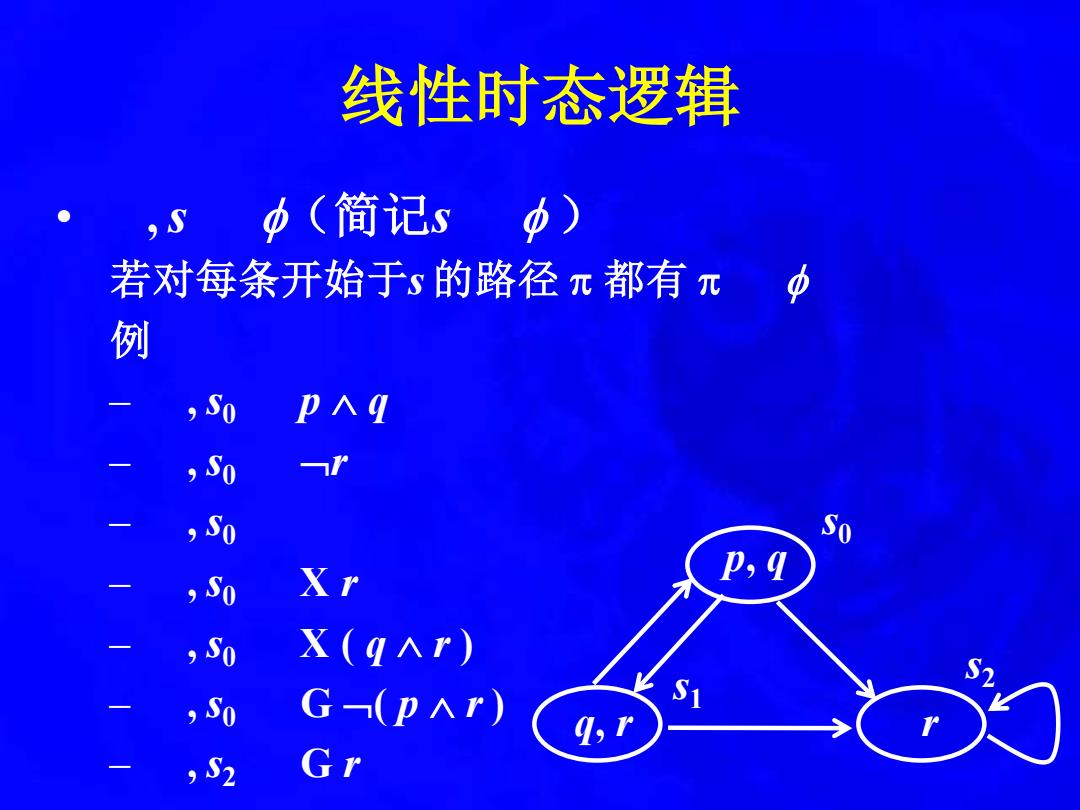
线性时态逻辑 • , s (简记s ) 若对每条开始于s 的路径 都有 例 – , s0 p q – , s0 r – , s0 – , s0 X r – , s0 X ( q r ) – , s0 G ( p r ) – , s2 G r q, r r s0 s2 s1 p, q