第、章应力应变状态分析 平面应力态应力前 切应力 使微元或其局部顺 时针方向转动为正; 反之为负。 ⊙嘉大婆
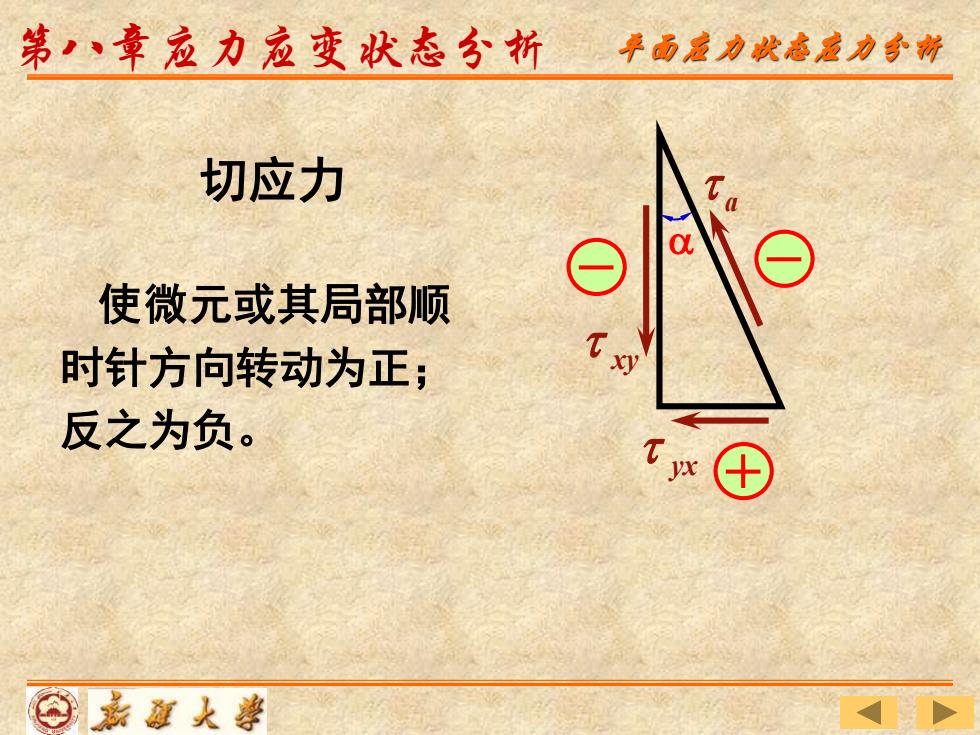
使微元或其局部顺 时针方向转动为正; 反之为负。 a yx xy 切应力 第八章应力应变状态分析 平面应力状态应力分析
第、章应力应变状态分析 平面应力状态应力奇前 方向角a 由x正向反时针转到n 正向者为正;反之为负。 ⊙嘉面人善
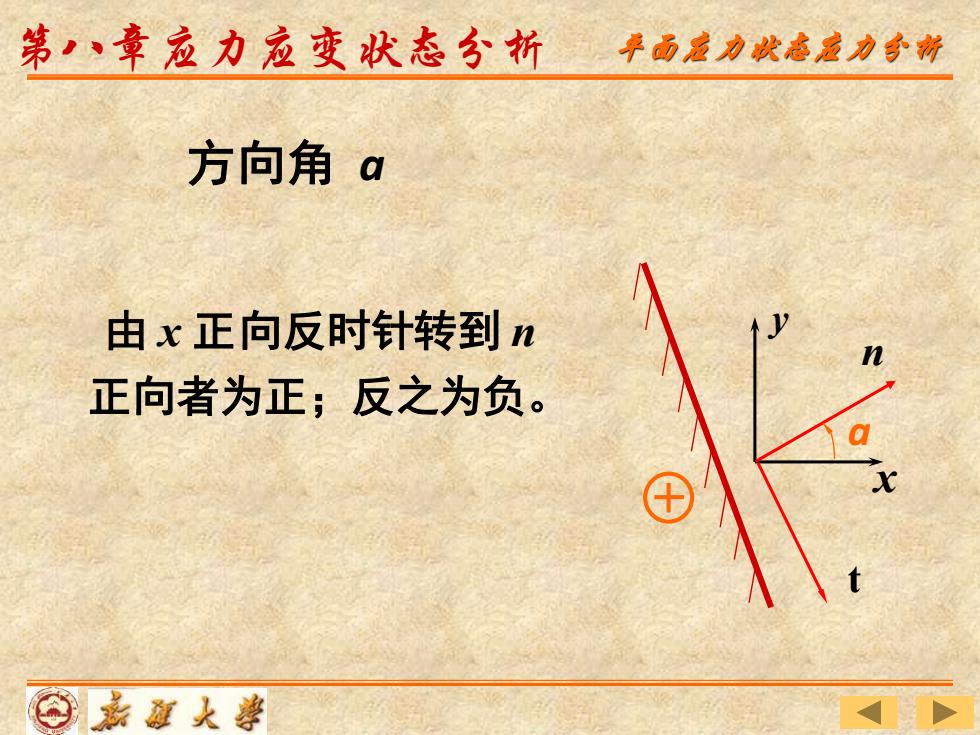
由 x 正向反时针转到 n 正向者为正;反之为负。 y x 方向角 a n t a 第八章应力应变状态分析 平面应力状态应力分析

第、章应力应变状态分析 平面龙力饮态应力今前 二、微元局部的平衡方程 ∑Fn=0 oa dA-(dAcosa)cosa (dcos)sin(dsinc)co -o (dAsina)sina =0 =o cos2a+o sin a-2t sinacosa ⊙嘉道大事
n a Fn = 0 - x (dAcos)cos - y (dAsin )sin = 0 xy y yx a dA + xy(dAcos)sin +yx (dAsin) cos a x σ 二、微元局部的平衡方程 cos a sin a 2 xy sina cosa 2 y 2 a x = + - 第八章应力应变状态分析 平面应力状态应力分析 dA

第八章应力应变状态分析 平面痘力状态应力奇前 ∑E=0 t d4-(dAcosa)sina -t (dAcosa)cosa+(dAsina)sina +o,(dAsina)cosa =0 Ta=(os-o)sinacosa+(cos2 a-sin a) ⊙嘉面人尊
Ft = 0 a dA - x (dAcos )sin - xy (dAcos ) cos + y (dAsin) cos = 0 + yx (dAsin )sin a xy y yx t a x σ ( )sina cosa (cos a sin a ) 2 2 a = x - y + xy - 第八章应力应变状态分析 平面应力状态应力分析 dA

第、章应力应变状态分析 =ox cos2 a+oy sin a-2Ty sinacosa T=(ox-0)sinacosa+ts(cos2 a-sin2 a) 利用cos2a=(1+c0s2)/2, sin2 a=(1-cos2a)/2, sin2a=2 sina cosa。 得到平面应力状态下的一般公式:乙y ,=0+,0s2a-tnn2a 2 2 Ta- 0x-6y sin 2a+T cos 2a 2 ⊙嘉范大事
利用 cos2a=(1+cos2a)/2, sin2 a =(1-cos2a)/2, sin2a =2sina cosa 。 n t y yx a a xy x σ cos a sin a 2 xy sina cosa 2 y 2 a x = + - ( )sina cosa (cos a sin a ) 2 2 a = x - y + xy - 得到平面应力状态下的一般公式: cos 2 sin2 2 2 x y x y x y - - + + = sin2 cos 2 2 x y x y + - = 第八章应力应变状态分析 平面应力状态应力分析 dA