※牛顿定律只适用于惯性系 例2.1一细绳跨过一轴承光滑的定滑轮,绳的两端分别悬有质量为m,和m 的物体(m<m2),如图2.2所示设滑轮和绳的质量可忽略不计,绳不能伸长, 试求物体的加速度以及悬挂滑轮的绳中张力. 解分别以m,m2定滑轮为研究 对象,其隔离体受力如图2.2所示 5在内 对m,它在绳子拉力T及重力m8 的作用下以加速度a,向上运动,取 向上为正向,则有 T-mg=ma ① 对m,它在绳子拉力T及重力m,g作用下以加速度a,向下运动,以 向下为正方向,则有 m28-T3=m2a2 ② 首页上页下页退出
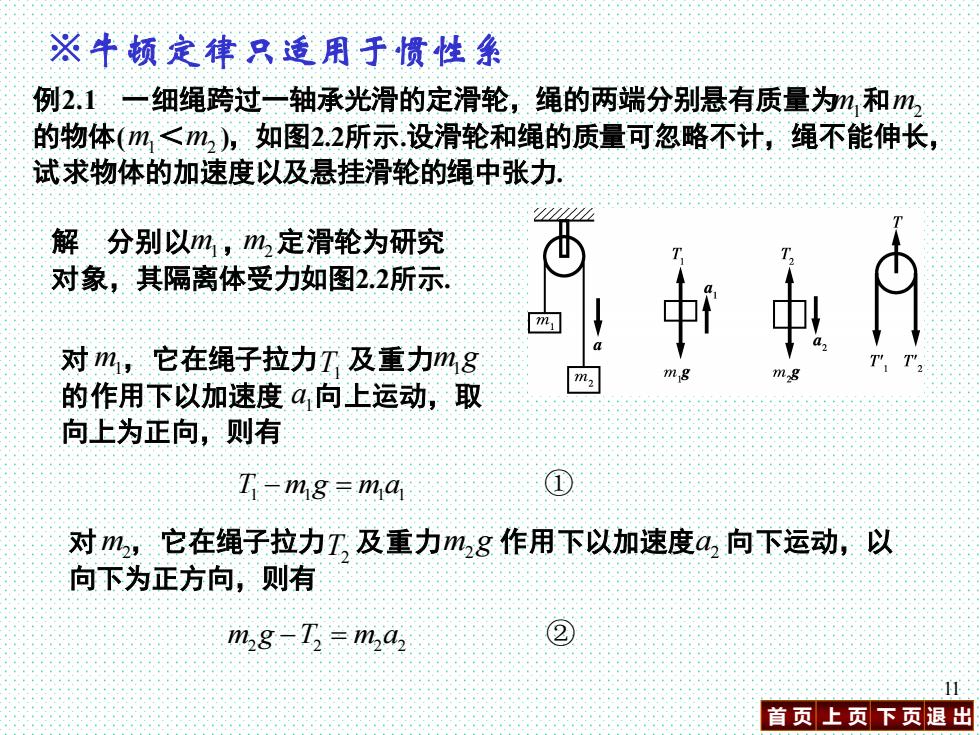
首 页 上 页 下 页 退 出 11 T m g m a 1 1 1 1 − = ① ※牛顿定律只适用于惯性系 例2.1 一细绳跨过一轴承光滑的定滑轮,绳的两端分别悬有质量为 和 的物体( < ),如图2.2所示.设滑轮和绳的质量可忽略不计,绳不能伸长, 试求物体的加速度以及悬挂滑轮的绳中张力. m1 m2 m1 m2 解 分别以 , 定滑轮为研究 对象,其隔离体受力如图2.2所示. m1 m2 对 ,它在绳子拉力 及重力 的作用下以加速度 向上运动,取 向上为正向,则有 m1 T1 m g1 1 a 对 ,它在绳子拉力 及重力 作用下以加速度 向下运动,以 向下为正方向,则有 m2 T2 m g2 2 a m g T m a 2 2 2 2 − = ②

由于定滑轮轴承光滑,滑轮和绳的质量可以略去,所以绳上各部分的张 力都相等;又因为绳不能伸长,所以m和m2的加速度大小相等,即有 T=T,=T,a=a,=a. 解①和②两式得 m-mg. T 2m m2g. m:+m, m1+m2 由牛顿第三定律知:T=工=T,T=T,=T,又考虑到定滑轮质量不 计,所以有 T=2T= 4m m2 m,+m2 容易证明 T'<(m:+m2)g 12 首页上页下页退出
首 页 上 页 下 页 退 出 12 由于定滑轮轴承光滑,滑轮和绳的质量可以略去,所以绳上各部分的张 力都相等;又因为绳不能伸长,所以 m1 和 m2 的加速度大小相等,即有 1 2 1 2 T T T a a a = = = = , . 解①和②两式得 2 1 1 2 1 2 1 2 m m 2m m . m +m m +m a g T g − = = , 由牛顿第三定律知: ,又考虑到定滑轮质量不 计,所以有 ' ' T T T T T T 1 1 2 2 = = = = , ' 1 2 1 2 4m m 2 m +m T T g = = 容易证明 ' 1 2 T g (m +m )

例2.2升降机内有一光滑斜面,固定在底板上,斜面倾角为0.当升降机 以匀加速度a1竖直上升时,质量为的物体从斜面顶端沿斜面开始下滑, 如图2.3所示.已知斜面长为l,求物体对斜面的压力,物体从斜面顶点滑到 底部所需的时间. 解以物体m为研究对象其受到 斜面的正压力N和重力mg以地为 参考系,设物体m相对于斜面的 加速度为42,方向沿斜面向下, 则物体相对于地的加速度为 a-a +a 设x轴正向沿斜面向下,轴正向垂直斜面向上,则对应用牛顿定律列 方程如下: x方向: mg sin=m(a,-a sine) y方向: N-mg cose ma cos0 13 首页上页下页退出
首 页 上 页 下 页 退 出 13 1 2 a a a = + 设x轴正向沿斜面向下,y轴正向垂直斜面向上,则对m应用牛顿定律列 方程如下: 例2.2 升降机内有一光滑斜面,固定在底板上,斜面倾角为θ.当升降机 以匀加速度 竖直上升时,质量为m的物体从斜面顶端沿斜面开始下滑, 如图2.3所示.已知斜面长为l,求物体对斜面的压力,物体从斜面顶点滑到 底部所需的时间. 1 a 解 以物体m为研究对象.其受到 斜面的正压力N和重力mg.以地为 参考系,设物体m相对于斜面的 加速度为 ,方向沿斜面向下, 则物体相对于地的加速度为 2 a 2 1 1 sin ( sin ) cos cos x mg m a a y N mg ma = − − = 方向: 方向:

解方程,得 a=(g+a)sing N =m(g+a)cos 由牛顿第三定律可知,物体对斜面的压力W与斜面对物体的压力W大 小相等,方向相反,即物体对斜面的压力为 m(g+a)cose 垂直指向斜面 因为m相对于斜面以加速度 a,=(g+a)sin 沿斜面向下作匀变速直线运动,所以 得 2L (g+a)sino 14 首页上页下页退出
首 页 上 页 下 页 退 出 14 解方程,得 2 1 1 ( )sin ( )cos a g a N m g a = + = + 由牛顿第三定律可知,物体对斜面的压力N′与斜面对物体的压力N大 小相等,方向相反,即物体对斜面的压力为 1 m g a ( )cos + 垂直指向斜面. 因为m相对于斜面以加速度 2 1 a g a = + ( )sin 沿斜面向下作匀变速直线运动,所以 2 2 2 1 1 1 ( )sin 2 2 l a t g a t = = + 得 ( 1 ) 2L g+ sin t a =

例2.3跳伞运动员在张伞前的俯冲阶段,由于受到随速度增加而增大的空 气阻力,其速度不会像自由落体那样增大当空气阻力增大到与重力相等时, 跳伞员就达到其下落的最大速度,称为终极速度.一般在跳离飞机大约10$, 下落约300~400m左右时,就会达到此速度(约50m/s).设跳伞员以鹰展姿 态下落,受到的空气阻力为 F(为常量),如图2.4(a)所示.试求跳伞 员在任一时刻的下落速度. 解跳伞员的运动方程为 mg-kv2=m dv dt 显然,在w2=g的条件下对应的速度即为终极速度,并用y,表示: mg 改写运动方程为 mdv kdt d ~dt -v2 15 首页上页下页退出
首 页 上 页 下 页 退 出 15 解 跳伞员的运动方程为 2 dv mg kv m dt − = 改写运动方程为 例2.3 跳伞运动员在张伞前的俯冲阶段,由于受到随速度增加而增大的空 气阻力,其速度不会像自由落体那样增大.当空气阻力增大到与重力相等时, 跳伞员就达到其下落的最大速度,称为终极速度.一般在跳离飞机大约10 s, 下落约300~400 m左右时,就会达到此速度(约50 m/s).设跳伞员以鹰展姿 态下落,受到的空气阻力为 (k为常量),如图2.4(a)所示.试求跳伞 员在任一时刻的下落速度. 2 F kv = 显然,在 kv mg 2 = 的条件下对应的速度即为终极速度,并用 vT 表示: T mg v k = 2 2 2 2 T T mdv v v kdt dv k dt v v m − = = −