
因=0时,v=0;并设时,速度为v,对上式两边取定积分: 、-山- 由基本积分公式得 是母 最后解得 -2gt _I-e r V l+eT 当1>时,vy 2g 16 首页上页下页退出
首 页 上 页 下 页 退 出 16 因t=0时,v=0;并设t时,速度为v,对上式两边取定积分: v t t 2 2 2 0 0 0 T T dv k g v v m v = = dt dt − 由基本积分公式得 T 2 T T T 1 g v v ln 2v v v v t + = − 最后解得 T T -2gt v 2gt T v 1-e v 1+e v − = 当 时, . 2 T v t g T v v →
设运动员质量m=70kg,测得终极速度V,=54m/s,则可推算出 k mg=0.24N2m21s 以此V值代入(①)的公式,可得到如图2.4(b)所示的-函数曲线 v/m's 60 ℃r54ms 2 0 51015202方 (b) 17 首页上页下页退出
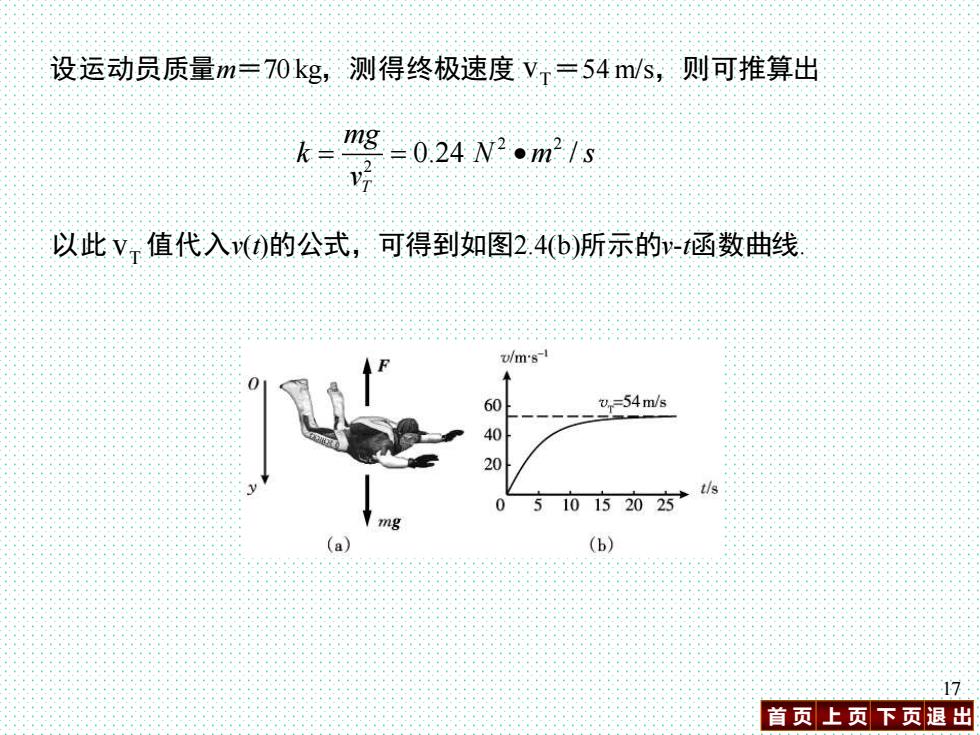
首 页 上 页 下 页 退 出 17 2 2 2 0.24 / T mg k N m s v = = • 设运动员质量m=70 kg,测得终极速度 vT =54 m/s,则可推算出 以此 值代入v(t)的公式,可得到如图2.4(b)所示的v-t函数曲线. T v

*2.1.5国际单位制和量纲(自学提纲) 1、单位制:基本量、导出量 单位制的任务是:规定哪些物理量是基本量及所使用的基本 量的数量级。 七个基本量为 长度、质量、时间、电流、温度、物质的量和发光强度 从基本量导出的量称为导出量,相应的单位称为导出单位。 2、S制中三个基本量的操作型定义 长度 1米=C× 299,792,458 时间 1秒=铯-133原子基态的两个超精细能级之间跃 迁时对应辐射的9,192,631,770个周期。 首页上页下页退出
首 页 上 页 下 页 退 出 18 1、 单位制:基本量、导出量 单位制的任务是:规定哪些物理量是基本量及所使用的基本 量的数量级。 七个基本量为 长度、质量、时间、电流、温度、物质的量和发光强度 2、 SI制中三个基本量的操作型定义 299,792,458 1 长度 1米=C 时间 1秒=铯-133原子基态的两个超精细能级之间跃 迁时对应辐射的9,192,631 ,770个周期。 从基本量导出的量称为导出量,相应的单位称为导出单位。 * 2.1.5 国际单位制和量纲(自学提纲)

质量 千克质量 3、量纲: 通过物理定律、定理、定义等将某个物理量表示成某种单位 制中基本物理量的方次。 因为导出量是由基本量导出的,所以导出量可用基本量的某 种组合(乘、除、幂等)表示。这种由基本量的组合来表示物 理量的式子称为该物理量的量纲式, 例如:在$制中 [-r- 19 首页上页下页退出
首 页 上 页 下 页 退 出 19 3、量纲: 因为导出量是由基本量导出的,所以导出量可用基本量的某 种组合(乘、除、幂等)表示。这种由基本量的组合来表示物 理量的式子称为该物理量的量纲式, 例如:在SI制中 −1 = = LT dt ds v −2 a = LT 通过物理定律、定理、定义等将某个物理量表示成某种单位 制中基本物理量的方次。 质量 千克质量

§2-2 非惯性系惯性力 我们知道牛顿定律只在惯性系中成立,可是,在实际问 题中,有时我们又必须在非惯性系中去观察和处理问题。那 么物理上如何解决这个问题的呢? 通过本节的讨论,我们将会看到,如果引入一个惯性力 的概念,那么我们在非惯性系中将仍可沿用牛顿定律的形式 而使问题得到简化。 20 首页上页下页退出
首 页 上 页 下 页 退 出 20 §2-2 非惯性系 惯性力 我们知道牛顿定律只在惯性系中成立,可是,在实际问 题中,有时我们又必须在非惯性系中去观察和处理问题。那 么物理上如何解决这个问题的呢? 通过本节的讨论,我们将会看到,如果引入一个惯性力 的概念,那么我们在非惯性系中将仍可沿用牛顿定律的形式 而使问题得到简化