
第三章随机向量 1.基本内容: 3.】二维随机变量及其联合分布函数 3.2二维离散型随机变量 3.3二维连续型随机变量 3.4随机变量的独立性 2.教学基本要求: 1、了解二维随机变量的概念 2、了解二维随机变量的联合分布函数及其性质,了解二维离散型随机变量的联合分布 律及其性质,了解二维连续型随机变量的联合概率密度及其性质,并会用它计算有关事件的 概率。 3、了解二维随机变量的边缘分布和条件分布, 4、理解随机变量独立性的概念,掌握应用随机变量的独立性进行概率计算。 3.教学重点:二维离散型、连续型随机变量及其概率分布问题。 教学难点:随机变量的条件分布和独立性, 4,教学建议:关于一维和多维的问题,是由简单到复杂的拓广和提升的过程。通常,一维 所研究的问题是简单的基础问题,而类似的多维问题是对一维问题的扩充与加深。关于一维 情形,我们研究了分布函数、分布律、概率密度函数等问题:而对二维问题,除了研究上述 问题外,还建立了边缘分布、边缘概率密度、条件分布和随机变量的独立性理论。 第四章随机变量函数的分布 1.基本内容: 4.1一维随机变量的函数 4.2两个随机变量的函数的分布 2.教学基本要求: 1、理解随机变量独立性的概念,掌握应用随机变量的独立性进行概率计算。 2、会求两个独立随机变量的简单函数的分布。 3教学重点:二维离散型随机变量的函数分布 教学难点:连续型随机变量的函数的分布, 4教学建议:关于两个随机变量的一些荷单函数的分布情况, 实际中遇到的函数是复杂多 样的,但一般的方法是:对离散型随机变量,从其联合分布律着手分析:对连续性随机变量, 则从分布函数或概率密度函数着手分析。 第五章 随机变量的数字特征 1.基本内容: 5.1数学期望 5.2方差与标准差 31
31 第三章 随机向量 1.基本内容: 3.1 二维随机变量及其联合分布函数 3.2 二维离散型随机变量 3.3 二维连续型随机变量 3.4 随机变量的独立性 2.教学基本要求: 1、了解二维随机变量的概念 2、了解二维随机变量的联合分布函数及其性质,了解二维离散型随机变量的联合分布 律及其性质,了解二维连续型随机变量的联合概率密度及其性质,并会用它计算有关事件的 概率。 3、了解二维随机变量的边缘分布和条件分布。 4、理解随机变量独立性的概念,掌握应用随机变量的独立性进行概率计算。 3.教学重点:二维离散型、连续型随机变量及其概率分布问题。 教学难点:随机变量的条件分布和独立性, 4.教学建议:关于一维和多维的问题,是由简单到复杂的拓广和提升的过程。通常,一维 所研究的问题是简单的基础问题,而类似的多维问题是对一维问题的扩充与加深。关于一维 情形,我们研究了分布函数、分布律、概率密度函数等问题;而对二维问题,除了研究上述 问题外,还建立了边缘分布、边缘概率密度、条件分布和随机变量的独立性理论。 第四章 随机变量函数的分布 1.基本内容: 4.1 一维随机变量的函数 4.2 两个随机变量的函数的分布 2.教学基本要求: 1、理解随机变量独立性的概念,掌握应用随机变量的独立性进行概率计算。 2、会求两个独立随机变量的简单函数的分布。 3.教学重点:二维离散型随机变量的函数分布。 教学难点:连续型随机变量的函数的分布, 4.教学建议:关于两个随机变量的一些简单函数的分布情况,实际中遇到的函数是复杂多 样的,但一般的方法是:对离散型随机变量,从其联合分布律着手分析;对连续性随机变量, 则从分布函数或概率密度函数着手分析。 第五章 随机变量的数字特征 1.基本内容: 5.1 数学期望 5.2 方差与标准差

5.3几种常见分布的数学期望与方差 5.4协方差与相关系数 55矩的基本概今 2.教学基本要求: 1、理解数字期望和方差的概念,掌握它们的性质与计算。 2、掌握二项分布、泊松分布和正态分布的数学期望和方差,了解均匀分布和指数分布 的数学期望和方差 3、会计算随机变量函数的数学期望。 4、了解矩、协方差和相关系数的概念与性质,并会计算。 3。教学重点:离散型、连续型随机变量的数字特征 教学难点:随机变量函数的数字特征 4.教学建议:数学期望的应用问题比较广泛,大家对“获利问题”、“等候问题”、“保 险问题”等要熟悉其中的解题关键和解题难道,达到“举一反三”的目的。加强离散型、连 续型随机变量数字特征的理论和方法的讲评,讲清随机变量函数的数字特征的计算公式。 第六章大数定律与中心极限定理 1.基本内容: 6.1大数定律 6.2中心极限定理 2.教学基本要求: 1、了解切比雪夫不等式。 2、了解切比雪夫大数定律和伯努利大数定律。 3、了解独立同分布的中心极限定理和棣莫佛拉普拉斯定理(二项分布以正态分布为极 限分布)。 3。教学重点:利用相关定理,尤其是了解切比雪夫大数定律、贝努里大数定律和同分布 中心极限定理近似计算有关事件的概率。 教学难点:大数定律和中心极限定理的内在含义。 4.教学建议:由大数定律可知,虽然频率可变,但当实验次数的增多,频率会在某个常数 周围稳 个常数 是事件发生的概率。中心极限定理表明,在相当一般条件下,当 随机变量的个数增加时,其和的分布趋于正态分布。 第七章数理统计的基本概念 1.基本内容: 7.1简单随机样本 72抽样分布 2.教学基本要求: 1、理解总体、个体、简单随机样本和统计量的概念,掌握样本均值、样本方差及样本
32 5.3 几种常见分布的数学期望与方差 5.4 协方差与相关系数 5.5 矩的基本概念 2.教学基本要求: 1、理解数字期望和方差的概念,掌握它们的性质与计算。 2、掌握二项分布、泊松分布和正态分布的数学期望和方差,了解均匀分布和指数分布 的数学期望和方差。 3、会计算随机变量函数的数学期望。 4、了解矩、协方差和相关系数的概念与性质,并会计算。 3.教学重点:离散型、连续型随机变量的数字特征 教学难点:随机变量函数的数字特征 4.教学建议:数学期望的应用问题比较广泛,大家对“获利问题”、“等候问题”、“保 险问题”等要熟悉其中的解题关键和解题难道,达到“举一反三”的目的。加强离散型、连 续型随机变量数字特征的理论和方法的讲评,讲清随机变量函数的数字特征的计算公式。 第六章 大数定律与中心极限定理 1.基本内容: 6.1 大数定律 6.2 中心极限定理 2.教学基本要求: 1、了解切比雪夫不等式。 2、了解切比雪夫大数定律和伯努利大数定律。 3、了解独立同分布的中心极限定理和棣莫佛-拉普拉斯定理(二项分布以正态分布为极 限分布)。 3.教学重点:利用相关定理,尤其是了解切比雪夫大数定律、贝努里大数定律和同分布 中心极限定理近似计算有关事件的概率。 教学难点:大数定律和中心极限定理的内在含义。 4.教学建议:由大数定律可知,虽然频率可变,但当实验次数的增多,频率会在某个常数 周围稳定下来,这个常数就是事件发生的概率。中心极限定理表明,在相当一般条件下,当 随机变量的个数增加时,其和的分布趋于正态分布。 第七章 数理统计的基本概念 1.基本内容: 7.1 简单随机样本 7.2 抽样分布 2.教学基本要求: 1、理解总体、个体、简单随机样本和统计量的概念,掌握样本均值、样本方差及样本

矩的计算。 2、了解X分布、1分布和F分布的定义及性质,了解分布分位数的概念并会查表计 算。 3、了解正态总体的某些常用统计量的分布。 3。教学重点:常用的统计量及其分布 教学难点:简单随机样本的特点,抽样分布的有关证明 4.教学建议:常用3大分布及相关性质,在数理统计中起者重要作用:而正态总体的样本 均值和样本方差的分布定理是统计推断的重要基础理论。 第八章参数估计 1.基本内容: 8.1点估计 8.2估计量的评价标准 8.3区间估计 2.教学基本要求: 1、理解点估计的概念 2、掌握矩估计法和极大似然估计法 3、了解估计量的评选标准(无偏性、有效性、一致性) 4、理解区间估计的概念 5、会求单个正态总体的均值和方差的置信区间。 6、会求两个正态总体的均值差和方差比的置信区间。 3。教学重点:矩估计法和极大似然估计法,单个正态总体的均值和方差的置信区间 教学难点:估计量的有效性、一致性评选标准 个或多个 体参数的置信区间是最完善的应用也最广泛。在构造正态总体参数的置信区间的过程中, 分布、x分布、F分布以及标准正态分布N0,)扮演了重要角色.由于正态分布具有对称性 到位数来计算未知参数的置信度为一的置信区间,其区间长度在所有这类区回 第九章假设检验 1.基本内容 9.1假设检验的基本概念 9.2单个正态总体的假设检验 9,3两个正态总体的假设检验 9.4总体分布X检验法 2.教学基本要求: 33
33 矩的计算。 2、了解 2 分布、 t 分布和 F 分布的定义及性质,了解分布分位数的概念并会查表计 算。 3、了解正态总体的某些常用统计量的分布。 3.教学重点:常用的统计量及其分布 教学难点:简单随机样本的特点,抽样分布的有关证明 4.教学建议:常用 3 大分布及相关性质,在数理统计中起着重要作用;而正态总体的样本 均值和样本方差的分布定理是统计推断的重要基础理论。 第八章 参数估计 1.基本内容: 8.1 点估计 8.2 估计量的评价标准 8.3 区间估计 2.教学基本要求: 1、理解点估计的概念 2、掌握矩估计法和极大似然估计法 3、了解估计量的评选标准(无偏性、有效性、一致性) 4、理解区间估计的概念 5、会求单个正态总体的均值和方差的置信区间。 6、会求两个正态总体的均值差和方差比的置信区间。 3.教学重点:矩估计法和极大似然估计法,单个正态总体的均值和方差的置信区间 教学难点:估计量的有效性、一致性评选标准 4.教学建议:在实际问题中, 当所研究的总体分布类型已知, 但分布中含有一个或多个未 知参数时, 如何根据样本来估计未知参数,这就是参数估计问题. 与其他总体相比, 正态总 体参数的置信区间是最完善的,应用也最广泛。在构造正态总体参数的置信区间的过程中,t 分布、 2 分布、F 分布以及标准正态分布 N(0,1) 扮演了重要角色. 由于正态分布具有对称性, 利用双侧分位数来计算未知参数的置信度为 1 的置信区间, 其区间长度在所有这类区间 中是最短的. 第九章 假设检验 1.基本内容: 9.1 假设检验的基本概念 9.2 单个正态总体的假设检验 9.3 两个正态总体的假设检验 9.4 总体分布 2 检验法. 2.教学基本要求:
1、理解显著性检验的基本思想,掌握假设检验的基本步骤,了解假设检验可能产生的 两类错误。 2、了解单个及两个正态总体的均值和方差的假设检验。 3、了解假设的X检验法 3。教学重点:正态总体的假设检验教学难点:总体分布的X检验法 :,老学建议:我们更提据样本所提供的信息以及运用话当的统计量对提出的假设作出越 验。 所有单参数假设检验的内容也适用于多参数与非参数假设检验问想,对多参数假设检 验问题,要寻求一个包含所有待检验参数的检验统计量,使之服从一个已知的确定分布。 四、教学环节与学时分配 教学内容 其 备注 讲课 习题课其他 第一章 64 2 第二章 64 3 第三章 86 2 4 第四幸 44 0 5 第五查 64 2 6 第六章 2 第业 就入步 第九查 10 总复可 五、教学中应注意的问题:无 六、实验/实践内容: 第一章、第二章、第三章配合课堂教学内容,每章安排一次习题课,第四章、第五章安 排一次习题课,第七章、第八章、第九章安排一次习题课。 七、考核方式: 见《概率论与数理统计B》课程考试大纲 八、教材及主要参考书: 1、选用教材: 《概率论与数理统计》,复旦大学出版社,廖茂新,廖基定主编,2011年8月。 2、主要参考书: 《概率论与数理统计》,浙江大学盛骤等编高等教有出版社,1989年8月。 34
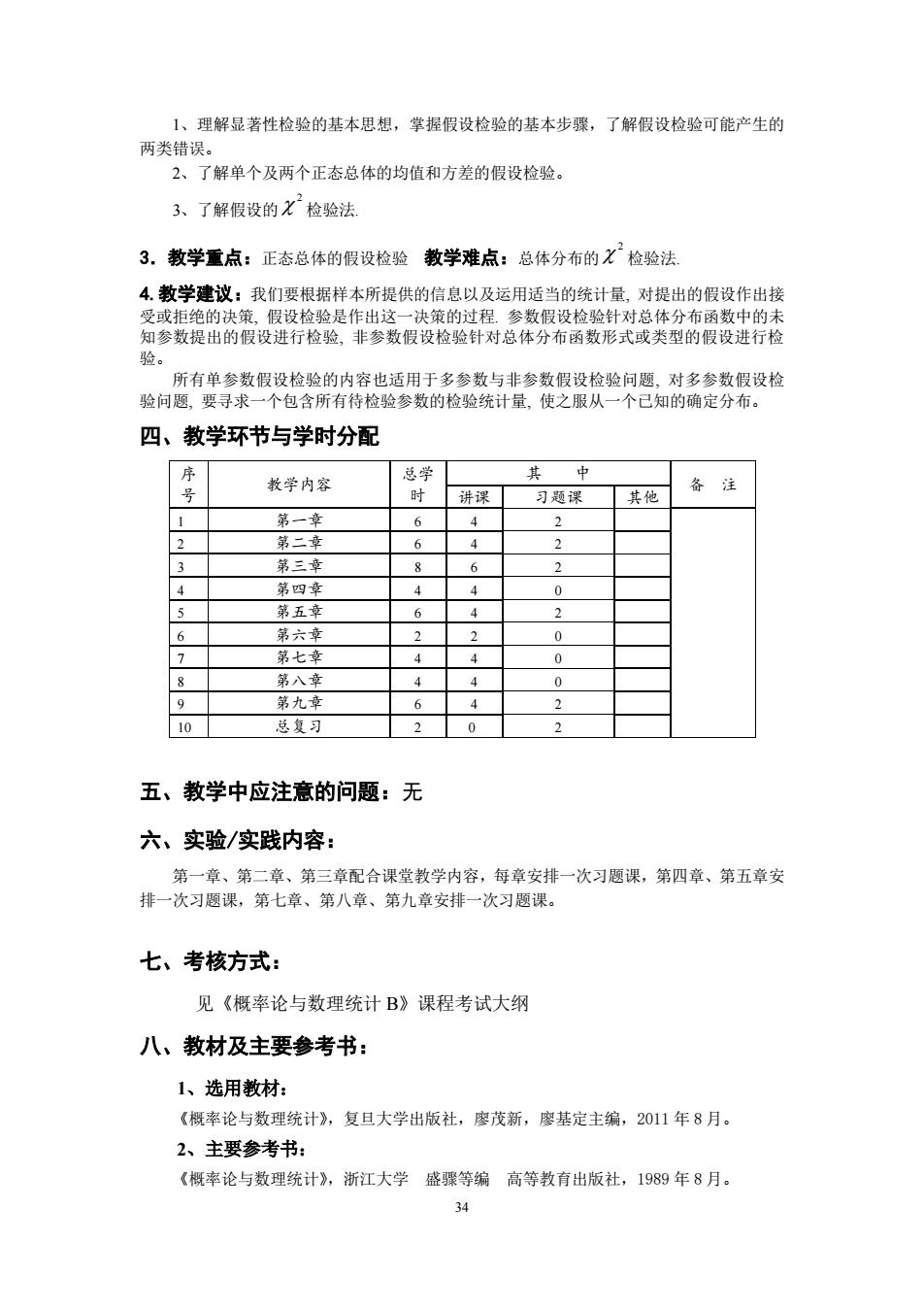
34 1、理解显著性检验的基本思想,掌握假设检验的基本步骤,了解假设检验可能产生的 两类错误。 2、了解单个及两个正态总体的均值和方差的假设检验。 3、了解假设的 2 检验法. 3.教学重点:正态总体的假设检验 教学难点:总体分布的 2 检验法. 4.教学建议:我们要根据样本所提供的信息以及运用适当的统计量, 对提出的假设作出接 受或拒绝的决策, 假设检验是作出这一决策的过程. 参数假设检验针对总体分布函数中的未 知参数提出的假设进行检验, 非参数假设检验针对总体分布函数形式或类型的假设进行检 验。 所有单参数假设检验的内容也适用于多参数与非参数假设检验问题, 对多参数假设检 验问题, 要寻求一个包含所有待检验参数的检验统计量, 使之服从一个已知的确定分布。 四、教学环节与学时分配 序 号 教学内容 总学 时 其 中 备 注 讲课 习题课 其他 1 第一章 6 4 2 2 第二章 6 4 2 3 第三章 8 6 2 4 第四章 4 4 0 5 第五章 6 4 2 6 第六章 2 2 0 7 第七章 4 4 0 8 第八章 4 4 0 9 第九章 6 4 2 10 总复习 2 0 2 五、教学中应注意的问题:无 六、实验/实践内容: 第一章、第二章、第三章配合课堂教学内容,每章安排一次习题课,第四章、第五章安 排一次习题课,第七章、第八章、第九章安排一次习题课。 七、考核方式: 见《概率论与数理统计 B》课程考试大纲 八、教材及主要参考书: 1、选用教材: 《概率论与数理统计》,复旦大学出版社,廖茂新,廖基定主编,2011 年 8 月。 2、主要参考书: 《概率论与数理统计》,浙江大学 盛骤等编 高等教育出版社,1989 年 8 月

《哈尔滨理工大学数学学习指导·概率论与数理统计》,哈尔滨理工大学数学系编写。 《概率论与数理统计》,由哈尔滨理工大学赵辉副教授主编,东北林业大学出版,2000 年1月 率论与数理统计》,哈尔滨工业大学曹彬等编哈尔滨工业大学出版社 九、教改说明及其他:无 执笔人:刘邵容系室审核人:王恒太
35 《哈尔滨理工大学数学学习指导 概率论与数理统计》,哈尔滨理工大学数学系编写。 《概率论与数理统计》,由哈尔滨理工大学赵辉副教授主编,东北林业大学出版,2000 年 1 月 《概率论与数理统计》,哈尔滨工业大学 曹彬等编 哈尔滨工业大学出版社 九、教改说明及其他:无 执笔人:刘邵容 系室审核人:王恒太