上海交通大学：《电力系统优化运行与市场化 Optimized Operation and Marketization of Power Systems》教学资源_教学资料_The structure and operation of the energy market 能量市场运行及补充资料（英文）

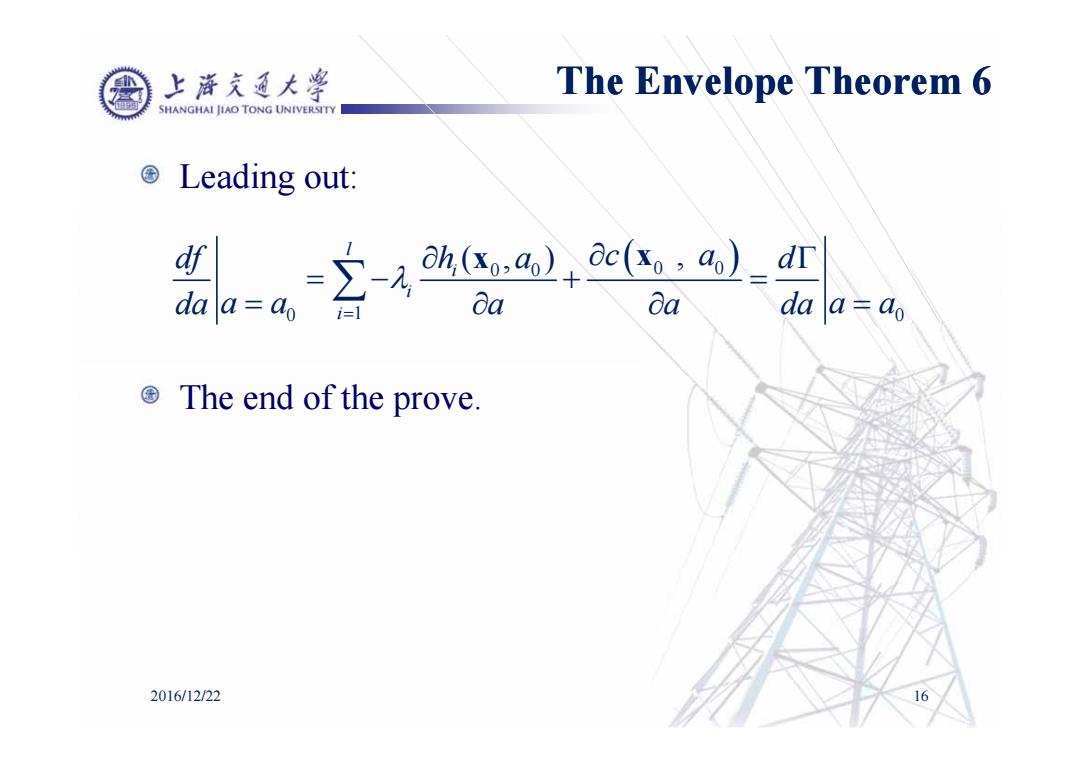
h 上游充廷大￥ The Envelope Theorem 6 SHANGHAI IIAO TONG UNIVERSITY ©Leading out: oc(xo,ao)_dr da Da da a=ao ©The end of the prove.. 2016/12/22

Leading out: The end of the prove. 2016/12/22 16 0 0   0 0 0 0 1 (,) , l i i i df d h a c a da a a da aa aa              x x The Envelope Theorem 6

上游充廷大￥ Seeing the Uniform-Pricing model SHANGHAI IIAO TONG UNIVERSITY from the perspective of the load From the envelope theorem,we can obtain: dc ar =-入=p(PD=∑P) Pp refers to the load demand The price is relevant to the load demand,when the load demand is certain,the price is equal to the micro increase rate of the power purchase cost. 2016/12/22

From the envelope theorem, we can obtain: refers to the load demand The price is relevant to the load demand, when the load demand is certain , the price is equal to the micro increase rate of the power purchase cost. 2016/12/22 17 Seeing the Uniform-Pricing model from the perspective of the load ) D D D Gi D D P P dc P P dP P            ܲ஽

h 上游充廷大￥ SHANGHAI IIAO TONG UNIVERSITY Example 1 Use K-K-T condition to solve the following 3-bus system: Min 10PGI+20PG2 +30PG3 P S.T. PG1+P2+P3=250 0≤P≤100 0≤P2≤200 0≤P3≤300 2016/12/22

Use K-K-T condition to solve the following 3-bus system: 2016/12/22 18 Example 1 123 123 1 2 3 10 20 30 . . 250 0 100 0 200 0 300 G GG G GG G G G G Min P P P S T PPP P P P           P

上游充廷大￥ SHANGHAI JIAO TONG UNIVERSITY solution: First,construct the Lagrangian function T=10P+20P2+30Pc3 +(Pa1+P2+Po3-250) +元(P1-100)+元2(P2-200)+(23300) PGI-72PG2-T3PG3 2016/12/22

solution： • First, construct the Lagrangian function 2016/12/22 19       123 123 11 2 2 33 11 2 2 33 10 20 30 250 100 200 300 GGG GG G GG G GGG PPP PPP PP P PPP                    

上游充廷大￥ SHANGHAI IIAO TONG UNIVERSITY Second,the optimality conditions are as follows 10+元+元1-t1=0,20+元+t2-2=0,30+元+T3-元3=0 PG1+PG2+Pa3=250 t1(PG1-100)=0,iP1=0 i2(P62-200)=0,i2P62=0 3(PG3-300)=0,i3Pg3=0 The optimal solution is P%1=100,P2=150,P63=0.p=-元=20 2016/12/22

• Second, the optimality conditions are as follows • The optimal solution is 2016/12/22 20       11 2 2 3 3 123 1 1 11 2 2 22 3 3 33 10 0, 20 0, 30 0 250 100 0, 0 200 0, 0 300 0, 0 GG G G G G G G G PP P P P P P P P                                                   123 100, 150, 0. 20 PPP GG G            