
上游充廷大¥ The Envelope Theorem 1 SHANGHAI IIAO TONG UNIVERSITY Optimal problem: f(a)=Min c(x,a) ST. h,(x,a)=0,(i=1,2,…,l) © The corresponding Lagrangian function: r=c(x,a)-∑h(x,a) 2016/12/22
Optimal problem: The corresponding Lagrangian function: 2016/12/22 11 The Envelope Theorem 1 , . . , 0, 1, 2, , i f a M in c a S T ha i l x x x 1 , , l i i i ca h a x x
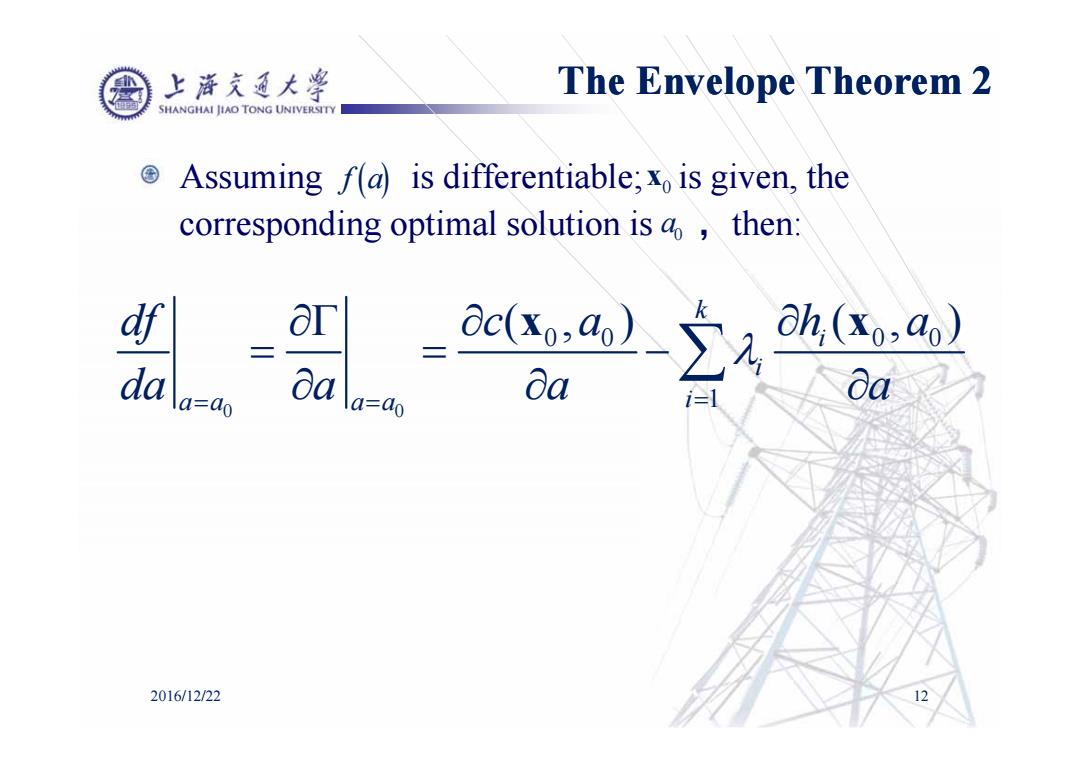
上游充通大¥ The Envelope Theorem 2 SHANGHAI IIAO TONG UNIVERSITY Assuming f(a)is differentiable;x is given,the corresponding optimal solution is a,then: df ar 三 aca)-2ha da \a=ao Da la=ao Ba i=1 2016/12/22
Assuming is differentiable; is given, the corresponding optimal solution is ,then: 2016/12/22 12 f a 0 a 0 x 0 0 00 00 1 (,) (,) k i i aa aa i df ca h a da a a a x x The Envelope Theorem 2

上游充廷大¥ The Envelope Theorem 3 SHANGHAI IIAO TONG UNIVERSITY ©Prove: ·Constraints: ·h,(x(a,a)=0 take the derivative of a on both sides ·ah,(K,a)k(a_oh(,a multiplied by A and summed Ox da Ba -立 =1 Ox da i=l Ba 2016/12/22
Prove: • Constraints: • take the derivative of a on both sides • multiplied by λ and summed 2016/12/22 13 00 0 00 1 1 ( ), 0 (, ) (, ) ( ) (,) () (,) i i i l l i i i i i i h aa ha ha d a da a h a da h a da a x x x x x xx x x The Envelope Theorem 3

上游充廷大¥ The Envelope Theorem 4 SHANGHAI IIAO TONG UNIVERSITY The Lagrangian function: T=c(区,a)-∑,h,(x,a) When a=ao,The optimal solution x0 satisfies the extremal condition,so: -空低 Ox 2016/12/22
• The Lagrangian function: • When a=a 0, The optimal solution x0 satisfies the extremal condition, so: 2016/12/22 14 1 , , l i i i ca h a x x 00 00 1 , , l i i i ca h a x x x x The Envelope Theorem 4

上游充廷大¥ The Envelope Theorem 5 SHANGHAI IIAO TONG UNIVERSITY ●Objective function: f(a)=c(x(a),a) when a=ao d斯 dc(xo,ao) h(a)+ac(aa da a=ao Ox da Ba 2融,a1.a)-2- Ch (xo-ao) i=l da i=1 Ba 2016/12/22
Objective function: 2016/12/22 15 0 00 00 0 0 ( ) ( ( ), ) , , ( ) fa c a a a a df ca ca d a da da a a a x x x x x when The Envelope Theorem 5 00 0 00 1 1 (,) () (,) l l i i i i i i h a da h a da a xx x x