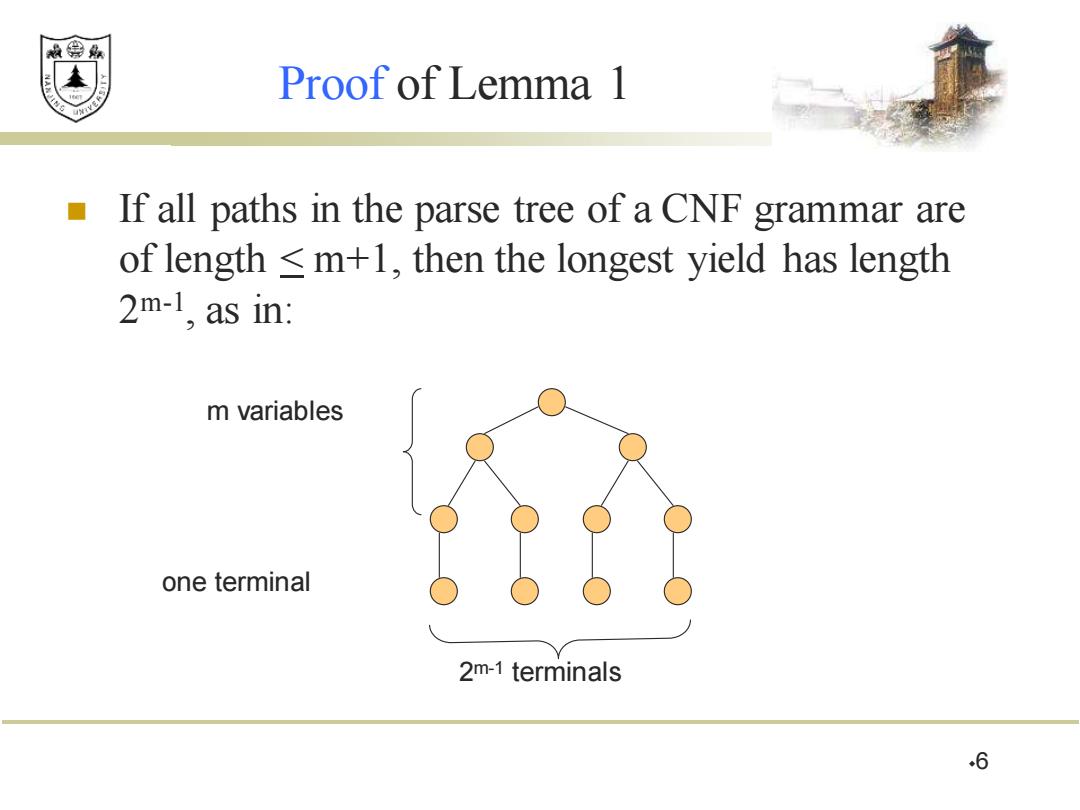
效绵鼎 Proof of Lemma 1 If all paths in the parse tree of a CNF grammar are of length m+1,then the longest yield has length 2m-1,as in: m variables one terminal 2m-1 terminals 6
Proof of Lemma 1 ◼ If all paths in the parse tree of a CNF grammar are of length < m+1, then the longest yield has length 2 m-1 , as in: 6 m variables one terminal 2 m-1 terminals

效绵县 Back to the Proof of the Pumping Lemma Now we know that the parse tree for z has a path with at least m+1 variables. Consider some longest path. There are only m different variables,so among the lowest m+1 we can find two nodes with the same label,say A. The parse tree thus looks like: 7
Back to the Proof of the Pumping Lemma ◼ Now we know that the parse tree for z has a path with at least m+1 variables. ◼ Consider some longest path. ◼ There are only m different variables, so among the lowest m+1 we can find two nodes with the same label, say A. ◼ The parse tree thus looks like: 7
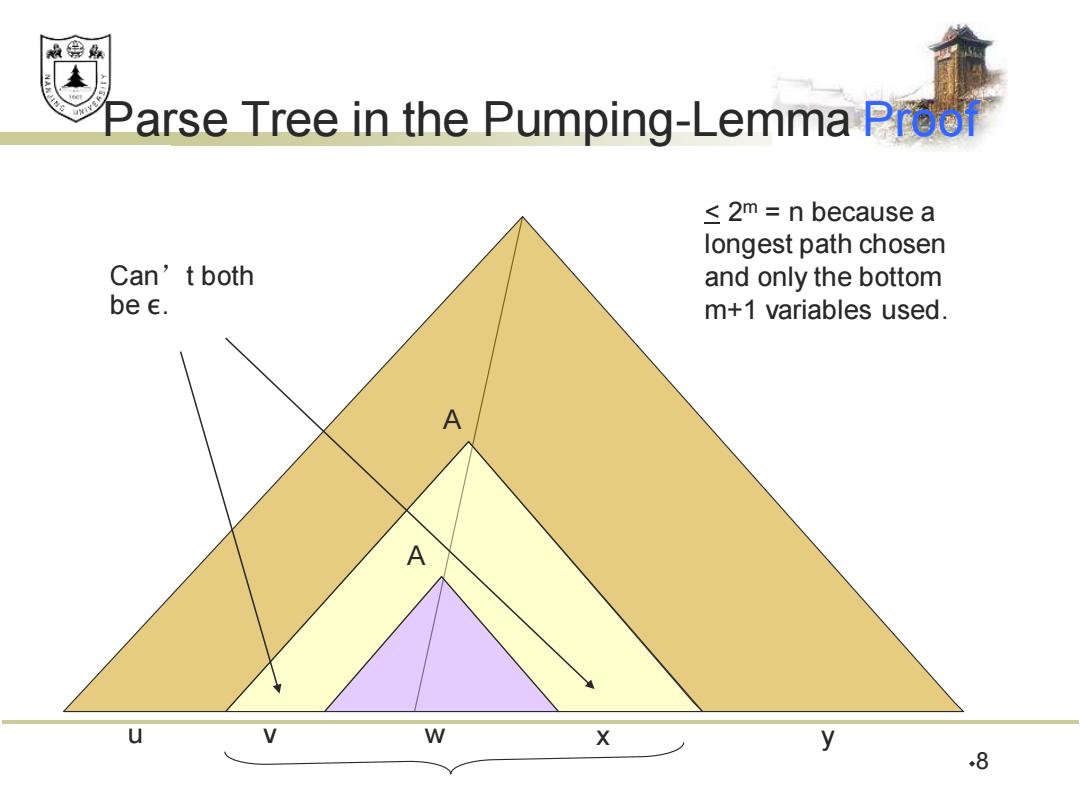
效绵易 Parse Tree in the Pumping-Lemma Preol ≤2m=n because a longest path chosen Can't both and only the bottom be c. m+1 variables used. A A V W X y 8
Parse Tree in the Pumping-Lemma Proof 8 < 2 m = n because a longest path chosen and only the bottom m+1 variables used. A A u v w x y Can’t both be ε
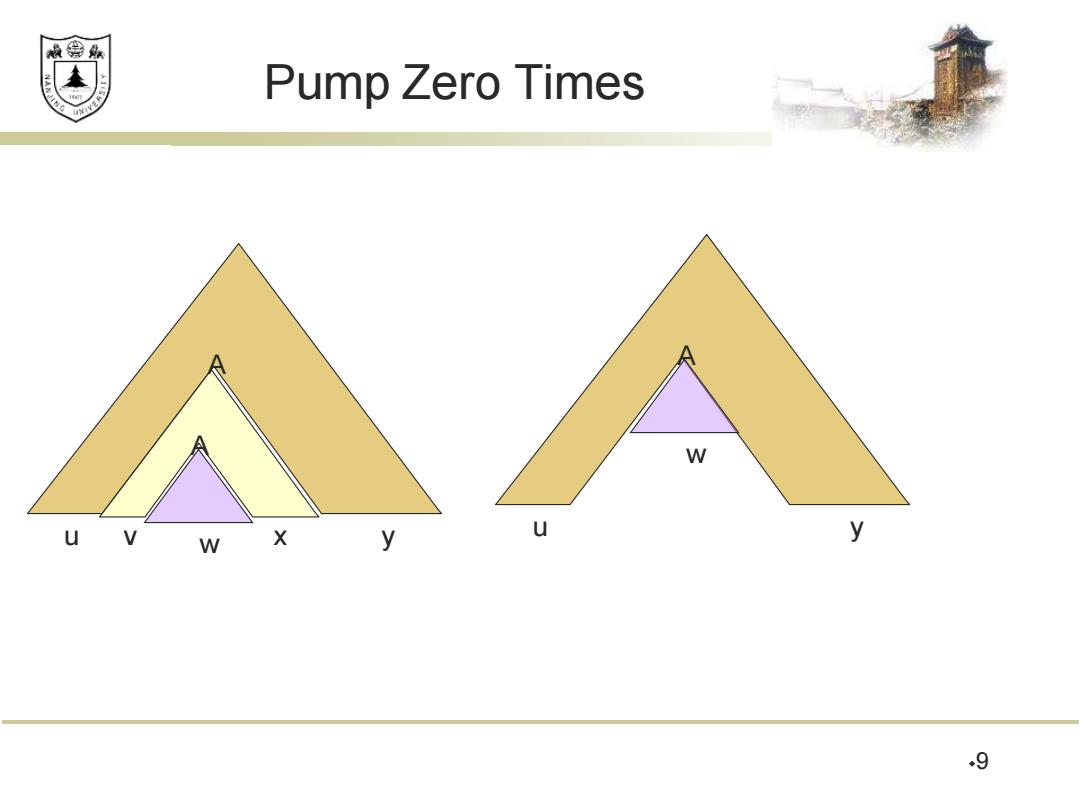
效绵鼎 Pump Zero Times A W U W X y y 9
Pump Zero Times 9 u y A v x A w u y A w
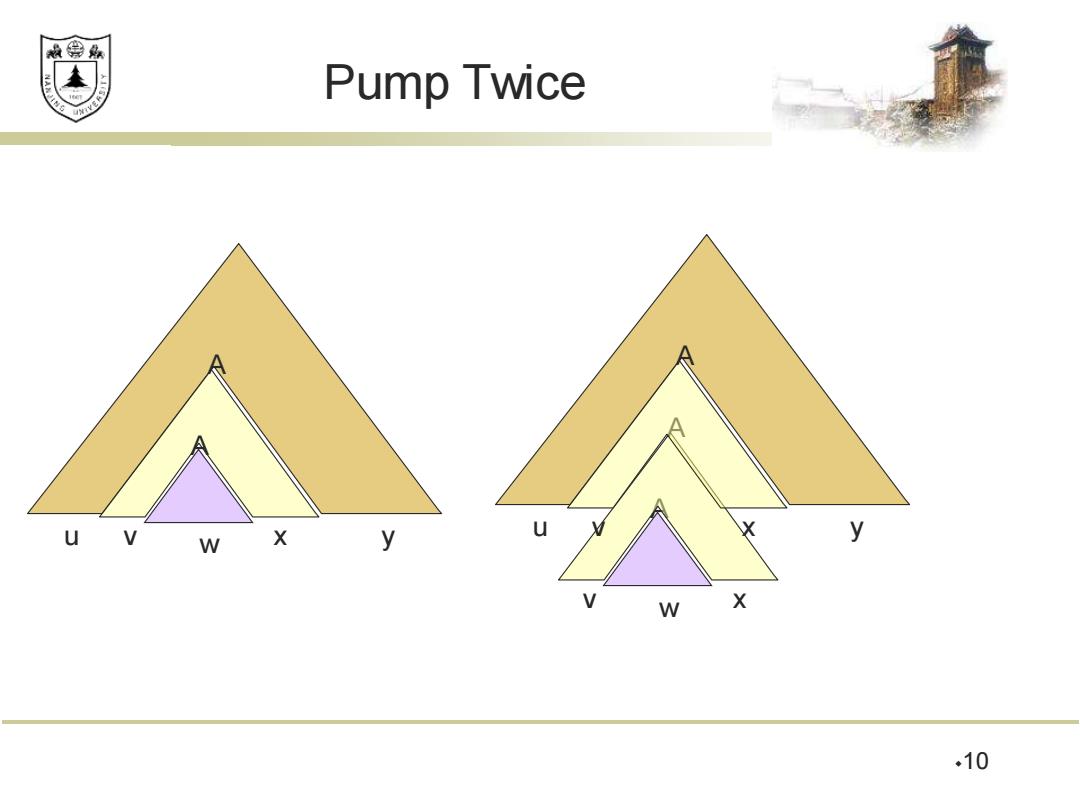
效绵鼎 Pump Twice W X y y W X .10
Pump Twice 10 u y A v x A w u y A w A v x A v x