
Correctness ■lfp1=p2,then p1(a1,…,an)=p2(a1,…,an) is always true,so the algorithm outputs p1= P2: If p p2:Let p p1-p2.Recall that 口we picked a1,,an←RSg{1,2,,100d, Lemma.Pp(au,ar)=0≤f o 口 So pi(a,..,an)=p2(a,...,an)wl prob.only 0.01. 口The algorithm outputs p1≠p2 w/prob.≥0.99. 11
Correctness ◼ If 𝑝1 = 𝑝2, then 𝑝1 𝑎1,… , 𝑎𝑛 = 𝑝2(𝑎1,…, 𝑎𝑛) is always true, so the algorithm outputs 𝑝1 = 𝑝2. ◼ If 𝑝1 ≠ 𝑝2: Let 𝑝 = 𝑝1 − 𝑝2. Recall that ❑ we picked 𝑎1, … , 𝑎𝑛 ←𝑅 𝑆 ≝ 1,2, …, 100𝑑 , ❑ Lemma. Pr𝑎𝑖←𝑅𝑆 𝑝 𝑎1,… , 𝑎𝑛 = 0 ≤ 𝑑 𝑆 . ❑ So 𝑝1 𝑎1,… , 𝑎𝑛 = 𝑝2(𝑎1,… , 𝑎𝑛) w/ prob. only 0.01. ❑ The algorithm outputs 𝑝1 ≠ 𝑝2 w/ prob. ≥ 0.99. 11

Catch One catch is that if the degree d is very large, then the evaluated value can also be huge. Thus unaffordable to write down. Fortunately,a simple trick called "fingerprint" handles this. Use a little bit of algebra;omitted here. Questions for the algorithm? 12
Catch ◼ One catch is that if the degree 𝑑 is very large, then the evaluated value can also be huge. ❑ Thus unaffordable to write down. ◼ Fortunately, a simple trick called “fingerprint” handles this. ❑ Use a little bit of algebra; omitted here. ◼ Questions for the algorithm? 12

Part 1:Examples Example 2:minimum cut 13
Part 1: Examples Example 2: minimum cut 13
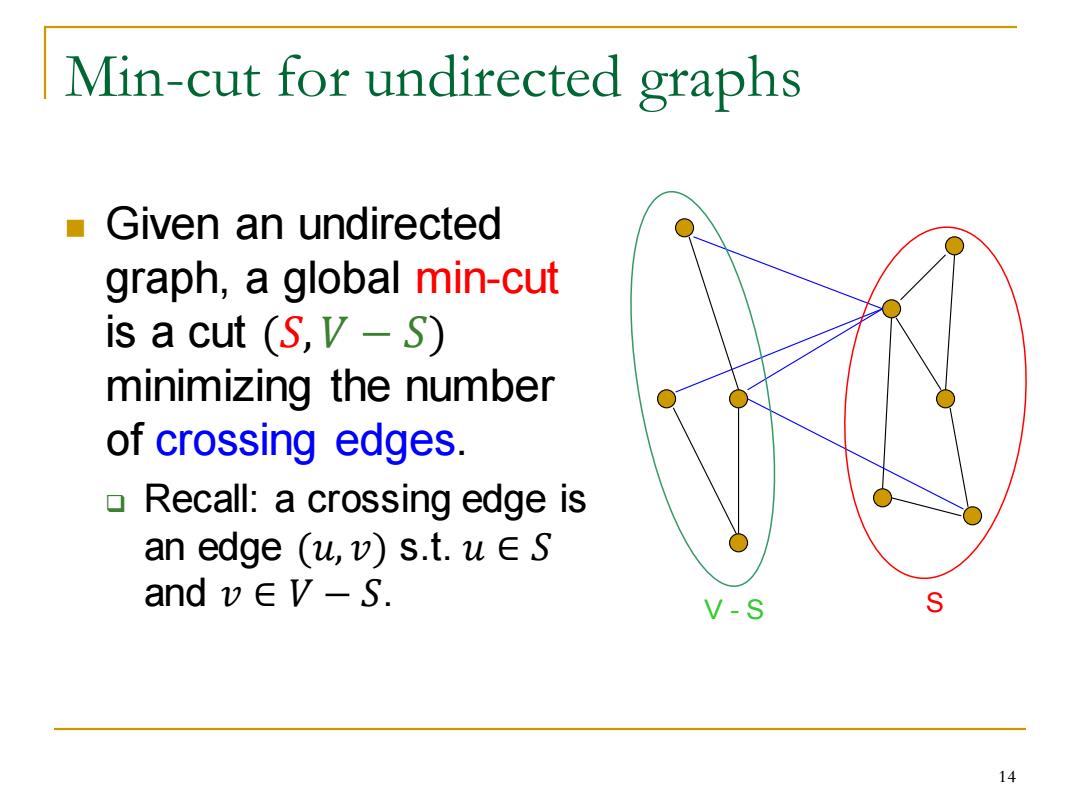
Min-cut for undirected graphs Given an undirected graph,a global min-cut is a cut (S,V-S) minimizing the number of crossing edges. Recall:a crossing edge is an edge (u,v)s.t.uES andv∈V-S. V-S S 14
Min-cut for undirected graphs ◼ Given an undirected graph, a global min-cut is a cut (𝑆, 𝑉 − 𝑆) minimizing the number of crossing edges. ❑ Recall: a crossing edge is an edge (𝑢, 𝑣) s.t. 𝑢 ∈ 𝑆 and 𝑣 ∈ 𝑉 − 𝑆. V - S S 14

A simple algorithm We'll introduce Karger's Contraction Algorithm. It's surprisingly simple. 15
A simple algorithm ◼ We’ll introduce Karger’s Contraction Algorithm. ◼ It’s surprisingly simple. 15