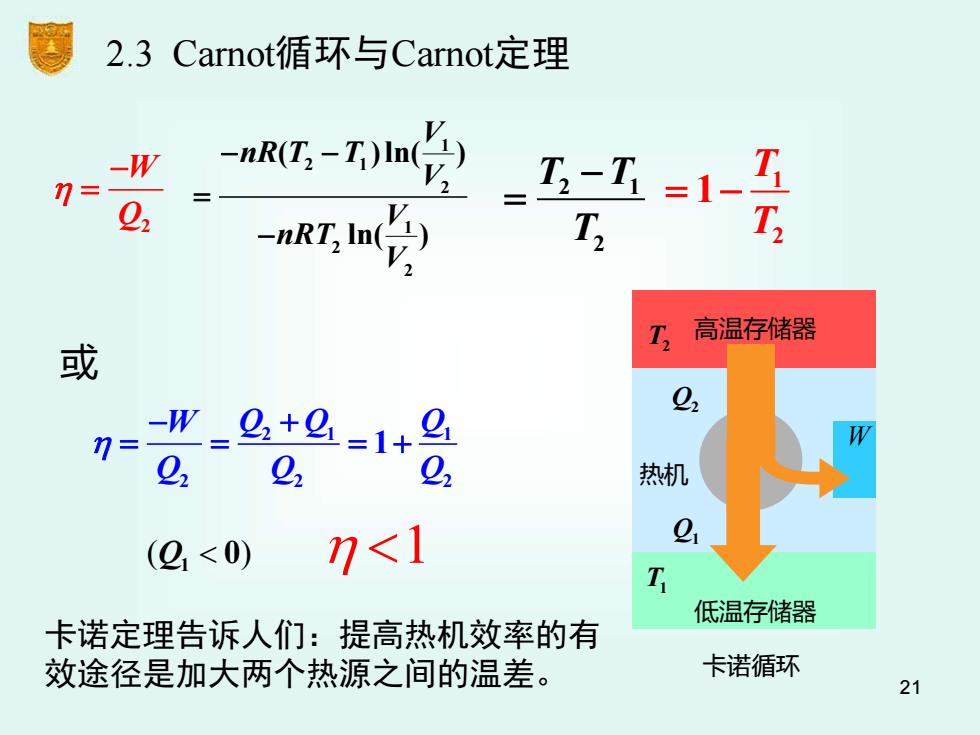
2.3 Carnot循环与Carnot定理 -不的 _五-五=1- 02 -nRr,a分) T T 高温存储器 或 1= _+=1+9 22 22 热机 (21<0) 7<1 低温存储器 卡诺定理告诉人们:提高热机效率的有 效途径是加大两个热源之间的温差。 卡诺循环 21
21 1 W Q2 − = 或 T T 1 2 = −1 卡诺循环 高温存储器 低温存储器 热机 T2 W T1 Q2 Q1 W Q Q Q Q Q Q 2 1 1 2 2 2 1 − + = = = + ( ) Q1 0 V nR T T V V nRT V 1 2 1 2 1 2 2 ( )ln( ) ln( ) − − = − 2 1 2 T T T − = 2.3 Carnot循环与Carnot定理 卡诺定理告诉人们:提高热机效率的有 效途径是加大两个热源之间的温差
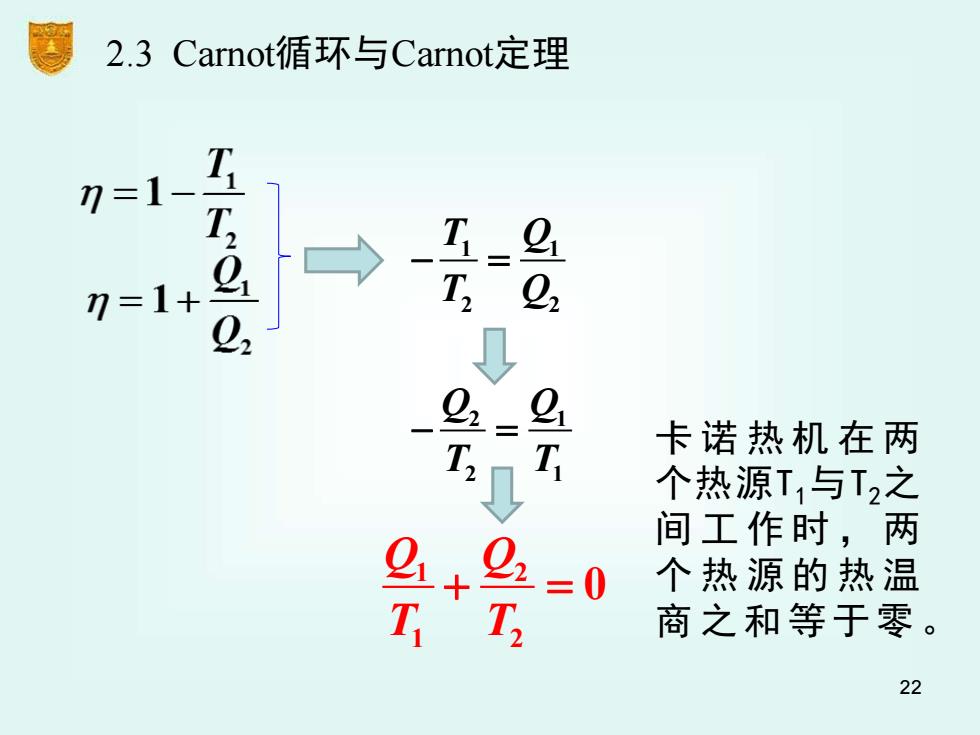
2.3 Carnot循环与Carnot定理 =1- T =1+ 3 22 22 73 卡诺热机在两 个热源T1与T2之 间工作时,两 =0 个热源的热温 T 商之和等于零。 22
22 T Q T Q 1 1 2 2 − = Q Q T T 2 1 2 1 − = Q Q T T 1 2 1 2 + = 0 2.3 Carnot循环与Carnot定理 卡 诺 热 机 在 两 个热源T1与T2之 间 工 作 时 , 两 个 热 源 的 热 温 商 之和 等于零

2.3 Carnot循环与Carnot定理 Carnot定理: 所有工作于同温热源和同温冷源之间的热机,其 效率都不能超过可逆机,即可逆机的效率最大。 Carnot定理推论: 所有工作于同温热源与同温冷源之间的可逆热机, 其热机效率都相等,即与热机的工作物质无关。 Carnot定理的意义: (1)引入了一个不等号7≤7R; (2)原则上解决了热机效率的极限值问题。 23
Carnot定理: Carnot定理推论: Carnot定理的意义: (2)原则上解决了热机效率的极限值问题。 (1)引入了一个不等号 I R ; 所有工作于同温热源和同温冷源之间的热机,其 效率都不能超过可逆机,即可逆机的效率最大。 所有工作于同温热源与同温冷源之间的可逆热机, 其热机效率都相等,即与热机的工作物质无关。 23 2.3 Carnot循环与Carnot定理
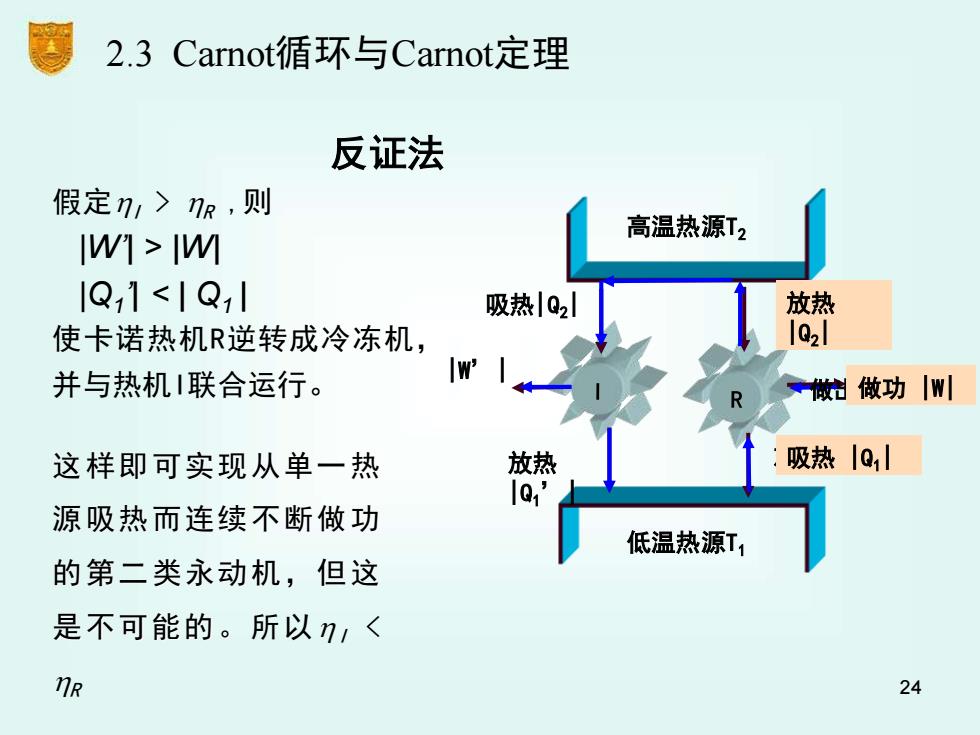
2.3 Carnot循环与Carnot定理 反证法 假定n,>nR,则 高温热源T2 W]>W 1Q11<1Q1 吸热|Q2l 放热 使卡诺热机R逆转成冷冻机, 并与热机联合运行。 Iw' *做始做功W川 这样即可实现从单一热 放热 吸热1Q 源吸热而连续不断做功 低温热源T1 的第二类永动机,但这 是不可能的。所以n,< nR 24
反证法 低温热源T1 高温热源T2 吸热|Q2 | 放热| Q1 | 做出| W | 吸热|Q2| 放热 |Q1’| |W’| 假定I > R ,则 |W’| > |W| |Q1 ’| < | Q1 | 使卡诺热机R逆转成冷冻机, 并与热机I联合运行。 吸热 |Q1| 放热 |Q2| 做功 |W| 这样即可实现从单一热 源吸热而连续不断做功 的第二类永动机,但这 是不可能的。所以 I < R 2.3 Carnot循环与Carnot定理 24

2.3 Carnot循环与Carnot定理 冷冻系数 如果将卡诺机倒开,就变成了致冷机。 这时环境对系统做功W,系统从低温热源(T)吸热Q,',而 放给高温热源(T2)O2的热量 将所吸的热与所作的功之比值称为冷冻系数,用B表示。 B 'T W T-T 式中W表示环境对系统所作的功。 25
冷冻系数 如果将卡诺机倒开,就变成了致冷机。 1 1 2 1 ' - Q T W T T = = 式中W表示环境对系统所作的功。 这时环境对系统做功W ,系统从低温热源(T1)吸热Q1 ′ ,而 放给高温热源(T2 )Q2 ′的热量 将所吸的热与所作的功之比值称为冷冻系数,用β表示。 2.3 Carnot循环与Carnot定理 25