
动画 化学势的狭义定义: 通常实验都是在等温、等压下进行,所以如不 特别指明,化学势就是指偏摩尔Gibbs自由能。 =( JT,p,n.(c≠B) 化学势在判断相变和化学变化的方向和限度方面 有重要作用。 山庆理工大学 空合>>】等温方程△,G⊙K,K,K⊙测定温度影响其他因素计算示例习题课
等温方程 rGm Kp Kx K测定 温度影响 其他因素 计算示例 习题课 动画 山东理工大学 B , , (c B) c B ( )T p n G n = 通常实验都是在等温、等压下进行,所以如不 特别指明,化学势就是指偏摩尔Gibbs自由能。 化学势在判断相变和化学变化的方向和限度方面 有重要作用。 化学势的狭义定义:

动画 化学势的应用 化学势判据: 条件:密闭系统,()xp,W0时 o,-交an{ <0正向自发 =0可逆或平衡 >0逆向自发 化学势是决定物质变化方向和限度的强度性质。 山庆东理工大学 合>等温方程△,G日K,KKe测定温度影响 其他因素计算示例习题课
等温方程 rGm Kp Kx K测定 温度影响 其他因素 计算示例 习题课 动画 山东理工大学 化学势的应用 化学势判据: 条件: 密闭系统,( )T, p , Wf=0时 i k i dG T p i dn = = 1 , ( ) <0 正向自发 =0 可逆或平衡 >0 逆向自发 化学势是决定物质变化方向和限度的强度性质
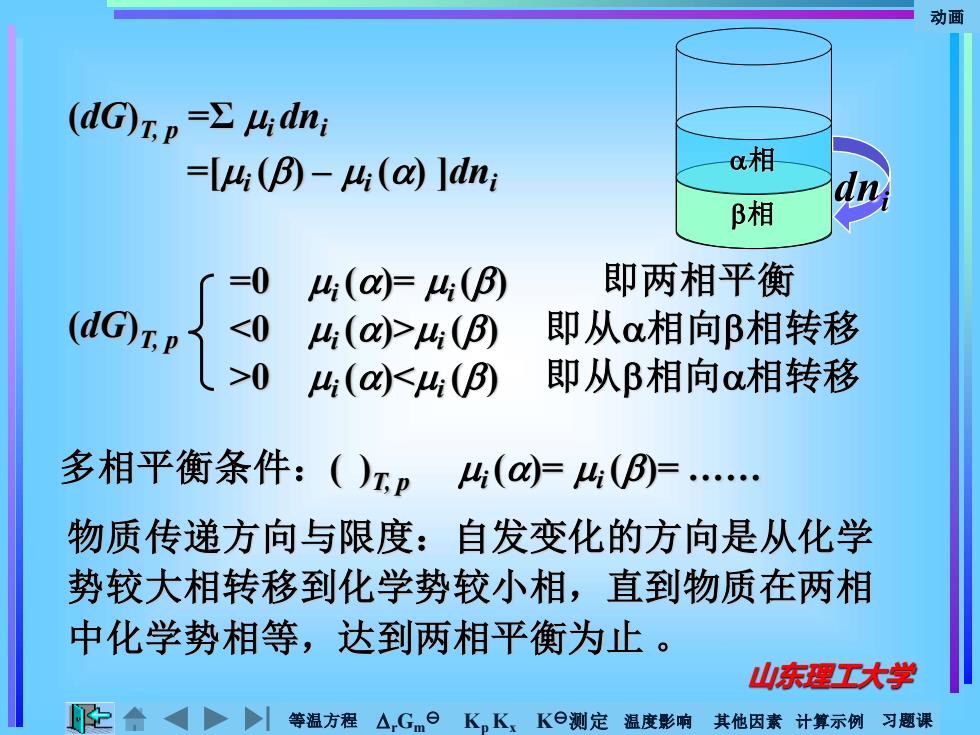
动画 (dG)xp=Σ4dn =l山(B-h(a网ldn a相 β相 d ©2 )4(=4(B) 即两相平衡 4(>4() 即从相向β相转移 4(a(B) 即从B相向o相转移 多相平衡条件:()p4(4(=. 物质传递方向与限度:自发变化的方向是从化学 势较大相转移到化学势较小相,直到物质在两相 中化学势相等,达到两相平衡为止。 山庆理工大学 合4>>等温方程△,G6 K,K、K⊙测定温度影响其他因素计算示例习题课
等温方程 rGm Kp Kx K测定 温度影响 其他因素 计算示例 习题课 动画 山东理工大学 (dG)T, p =Σ i dni =[i () – i () ]dni 物质传递方向与限度:自发变化的方向是从化学 势较大相转移到化学势较小相,直到物质在两相 中化学势相等,达到两相平衡为止 。 多相平衡条件:( )T, p i ()= i ()= . =0 i ()= i () 即两相平衡 <0 i ()>i () 即从相向相转移 >0 i ()<i () 即从相向相转移 (dG)T, p 相 相

动画 2、在化学平衡中的应用 例如()p反应S02(g)+1/202(g)=S03(g) dn(so2)1/2dn(o2) dn(so:) (dGxp=24dm,=4(S03)dn-4(S02)dm-1/2402)dn =4(s03)S02)-1/24(02)】dn L4S03)-4(S02)-1/24(02=0(dGxp=0 平衡 [4(S03)4S02)-1/24(02<0(dG)xp<0反应正向自发 I(S03)-4(S02)-124(02)>0(dGpp>0反应逆向自发 化学反应向化学势减小的方 =0:反应达平衡 向进行。反应前后化学势相 ∑y4 <0:反应正向自发 等时平衡。 >0:反应逆向自发 ∑V4(反应物)=∑y凸产物) 等温方程△,Gm9 K⊙测定温度影响其他因素计算示例习题课
等温方程 rGm Kp Kx K测定 温度影响 其他因素 计算示例 习题课 动画 山东理工大学 2、在化学平衡中的应用 例如( )T,p 反应 SO2 (g) + 1/2O2 (g)= SO3 (g) dn(SO2) 1/2dn(O2) dn(SO3) [(SO3)– (SO2)–1/2 (O2)]=0 (dG)T, p =0 平衡 [(SO3)– (SO2)–1/2 (O2)]<0 (dG)T, p <0 反应正向自发 [(SO3)– (SO2)–1/2 (O2)]>0 (dG)T , p >0 反应逆向自发 =0 : 反应达平衡 <0: 反应正向自发 >0: 反应逆向自发 (dG)T, p =Σ i dni= (SO3) dn–(SO2)dn- 1/2 (O2)dn = [(SO3)– (SO2)–1/2 (O2 )]dn ∑νi i 化学反应向化学势减小的方 向进行。反应前后化学势相 等时平衡。 i i (反应物)= j j (产物)

动画 纯理想气体的化学势 只有一种理想气体,山=( G) dG =-SdT+Vdp = %-6p-jg如 0,47p9)=b是 山庆理工大学 空合>l等温方程△,G日K,K:Ke测定温度影响其他因素计算示例习题课
等温方程 rGm Kp Kx K测定 温度影响 其他因素 计算示例 习题课 动画 山东理工大学 纯理想气体的化学势 只有一种理想气体, T p n G , B ( ) = T T T p n G p p = , B ( ) ( ) T p T B p G n , ( ) = T p n V B , = =Vm d d d G S T V p = − + ( , ) ( , ) ln p T p T p RT p − = d d d m p p p p p p RT V p p p = =