山西能源学院：《传热学》课程教学资源（PPT课件）第七章 相变对流传热

山莎佛源李花 SHANXI INSTITUTE OF ENERGY Chap7相变对流换热 2基本假设：凝结液膜的流动和换热符合边界层的薄层性质。 1)二维、稳态、常物性、层流； 2)蒸气是静止的，汽液界面上无对液膜的粘滞应力； 3)液膜很薄且流动缓慢，惯性力可忽略，液膜流动只取决于 重力和粘滞力； 4)汽液界面上无温差，界面上液膜温度等于饱和温度，忽略 汽液界面热阻； 5)膜内温度分布是线性的，即认为液膜内的热量转移只有导 热，而无对流作用： 6)液膜的过冷度可以忽略，认为液膜与蒸汽只有潜热交换无 显热换热； 7)pv<<pIi 8)液膜表面平整无波动

Chap7 相变对流换热 1）二维、稳态、常物性、层流； 2）蒸气是静止的，汽液界面上无对液膜的粘滞应力； 3）液膜很薄且流动缓慢，惯性力可忽略，液膜流动只取决于 重力和粘滞力； 4）汽液界面上无温差，界面上液膜温度等于饱和温度，忽略 汽液界面热阻； 5）膜内温度分布是线性的，即认为液膜内的热量转移只有导 热，而无对流作用； 6）液膜的过冷度可以忽略，认为液膜与蒸汽只有潜热交换无 显热换热； 7）v<<l； 8）液膜表面平整无波动。 2.基本假设：凝结液膜的流动和换热符合边界层的薄层性质

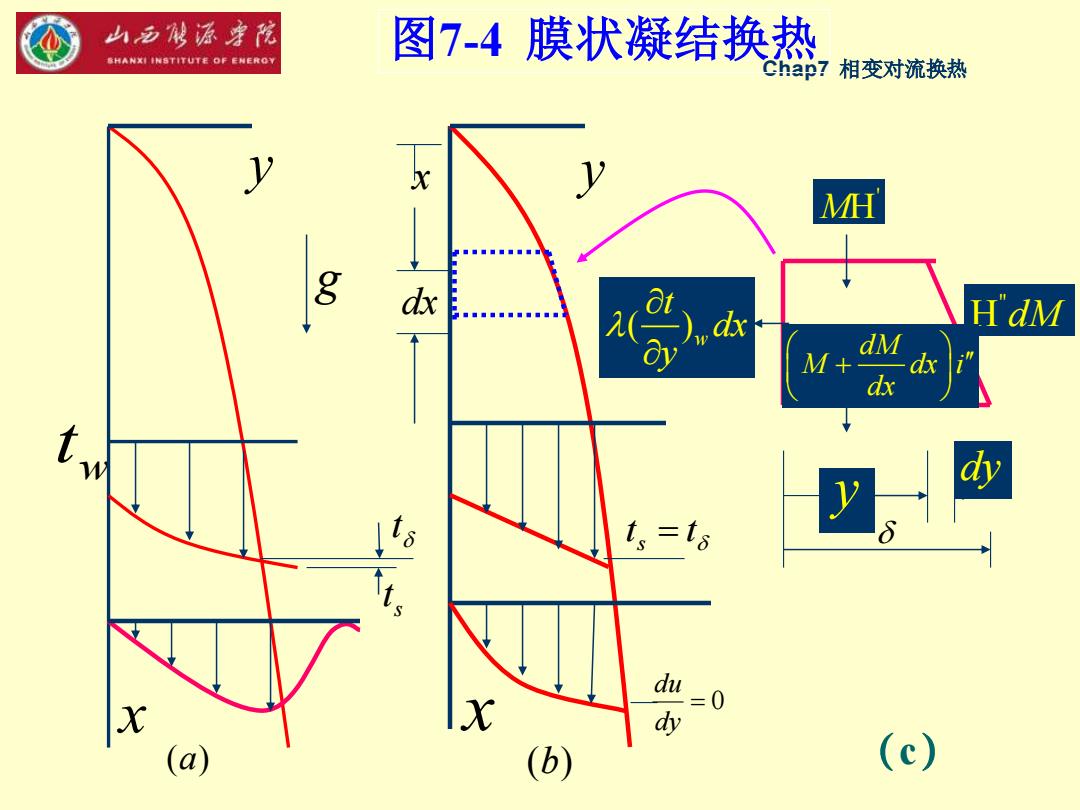
山西城源李院 图7-4膜状凝结换热 SHANXI INSTITUTE OF ENEROY han7 相变对流换热 1 MH g d H'dM dM M+ dx dx t,=18 du =0 X (a) (b) (c)

Chap7 相变对流换热 (a) w t y x g  t s t 图7-4 膜状凝结换热 (b) y x  t t s = = 0 dy du " H dM ' MH ( ) w t dx y    dM M dx i dx   +      y dy  （c） x dx

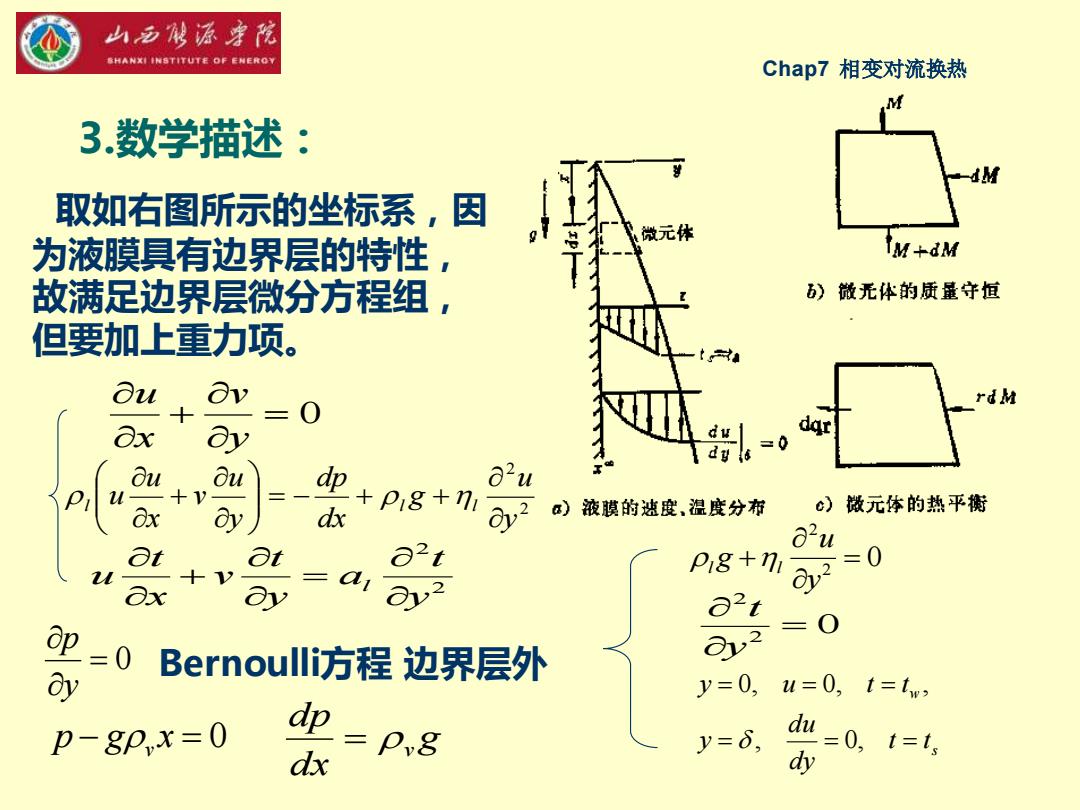
山多能源宇院 参HANXI INSTITUT老OF ENEROY Chap7相变对流换热 3.数学描述： 取如右图所示的坐标系，因 微元体 为液膜具有边界层的特性 IM+M 故满足边界层微分方程组， )微无体的质量守恒 但要加上重力项。 Ou Ov rdM ax ay dy ls u Ou u +V 8x 迎+pg+niy2 a)液摸的速度，度分布 c)微元体的热平衡 8u at at =0 +V ax =a1 pig 82t op =0 =0 Bernoulliz方程边界层外 @2 oy y=0, u=0,t=t p-gpx=0 dp dx =P,8 y=6, du=0,t=1, dy

Chap7 相变对流换热 取如右图所示的坐标系，因 为液膜具有边界层的特性， 故满足边界层微分方程组， 但要加上重力项。 = 0   +   y v x u 2 2 y t a y t v x t u l   =   +   2 2 y u g dx dp y u v x u l u l l   = − + +           +      = 0   y p Bernoulli方程 边界层外 p − gv x = 0 g dx dp = v 0 2 2 =   + y u l g l 2 0 2 =   y t s w t t dy du y y u t t = = = = = = , 0, 0, 0, ,  3.数学描述：

山多能源宇院 SHANXI INSTITUTE OF ENEROY Chap7相变对流换热 4.求解 du 8P1 y+c dy gPLy2+cy+c2 71 211 y=0,u=0→c2=0 du W=- dy\s 8P16+G=0 n 2n1 Ot ay =c1 t=cy+C2 +5- O,t=tw,C2=tw y=δ，t=t,t,=c6+tm(

Chap7 相变对流换热 1 y c g dy du l l = − +  1 2 2 2 y c y c g u ll = − + +  y = 0, u = 0  c 2 = 0 = − + c 1 = 0 g dy du l l    ) 21 ( 2 2 y y g u ll = −  −  c 1 yt =  1 2 t = c y + c w w y = t = t c = t 2 0, , s s w y =  t = t t = c  + t 1 , ,  s w t t c − 1 = ( ) w s w t t y t = t + −  4. 求解

山多能源宇院 参HANXI INSTITUT老OF ENEROY chap7相变对流换热 通过x=截面处宽为1m的壁面凝结液体的质量流量为 M-a1-p=e-护内 传-r 371 X+dx处质量流量的增加 dM 8p,282d6 M+M 71 )微无体的质量牛恒 对微元体应用热力学第一定律 rdM=dΦ rdM 即 r8d6-, ,ts一twdx c)微元体的热平衡 71

Chap7 相变对流换热 y y dy g M dM udy l l l       = = = −    2 0 0 2 0 2 1        l l l l g y y g        6 3 1 2 1 2 3 0 2 3 2  =            = − X+dx 处质量流量的增加 l g l d dM     2 2 = 对微元体应用热力学第一定律 d x rdM =  dx g d t t r s w l l l       − = 即 2 2 通过x=l截面处宽为1m的壁面凝结液体的质量流量为