
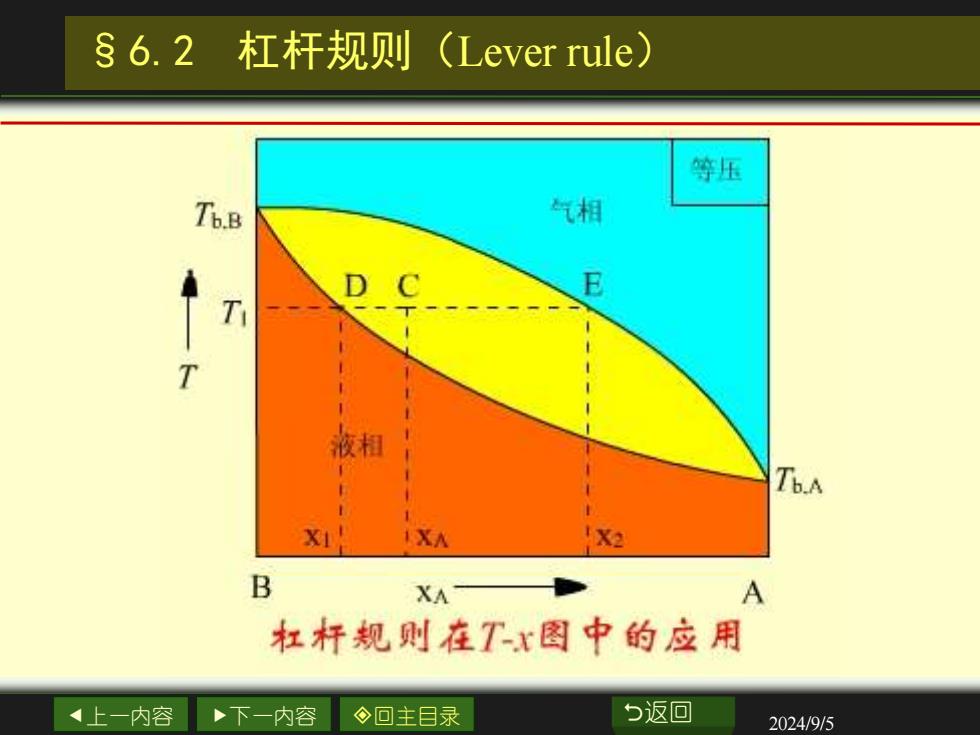
§6.2杠杆规则 (Lever rule) 讨论A,B二组分系统,气、液两相,C点代表了系 统总的组成和温度,称为物系点。 通过C点作平行于横坐标 等压 气相 的等温线,与液相和气相线 Tb.B 分别交于D点和E点。DE线称 T 为等温连结线(tie line)。 液粗 b.A 落在DE线上所有物系点 XA X2 的对应的液相和气相组成, B XA 杠杆规则在Tx图中的应用 都由D点和E点的组成表示。 4上一内容 下一内容 ◇回主目录 与返回 2024/9/5
上一内容 下一内容 回主目录 返回 2024/9/5 §6.2 杠杆规则(Lever rule) 讨论A,B二组分系统,气、液两相,C点代表了系 统总的组成和温度,称为物系点。 通过C点作平行于横坐标 的等温线,与液相和气相线 分别交于D点和E点。DE线称 为等温连结线(tie line)。 落在DE线上所有物系点 的对应的液相和气相组成, 都由D点和E点的组成表示
§6.2 杠杆规则 (Lever rule) 等压 To.B 气相 T T ToA IXA B XA A 杠杆规则在Tx图中的应用 上一内容 下一内容 ◇回主目录 与返回 2024/9/5
上一内容 下一内容 回主目录 返回 2024/9/5 §6.2 杠杆规则(Lever rule)

§6.2杠杆规则 (Lever rule) 液相和气相的数量借助于力学中的杠杆规则求算, 即以物系点为支点,支点两边连结线的长度为力矩,计 算液相和气相的物质的量或质量,这就是可用于任意两 相平衡区的杠杆规则。即 等压 相 n(1).CD=n(g).CE D 或 m(I).CD=m(g).CE 液相 可以用来计算两相的相对量 XA (总量未知)或绝对量(总 XA 杠杆规则在Tx图中的应用 量已知)。 4上一内容 下一内容 ◇回主目录 与返回 2024/9/5
上一内容 下一内容 回主目录 返回 2024/9/5 §6.2 杠杆规则(Lever rule) 液相和气相的数量借助于力学中的杠杆规则求算, 即以物系点为支点,支点两边连结线的长度为力矩,计 算液相和气相的物质的量或质量,这就是可用于任意两 相平衡区的杠杆规则。即 n n (l) CD (g) CE = 或 m m (l) CD (g) CE = 可以用来计算两相的相对量 (总量未知)或绝对量(总 量已知)
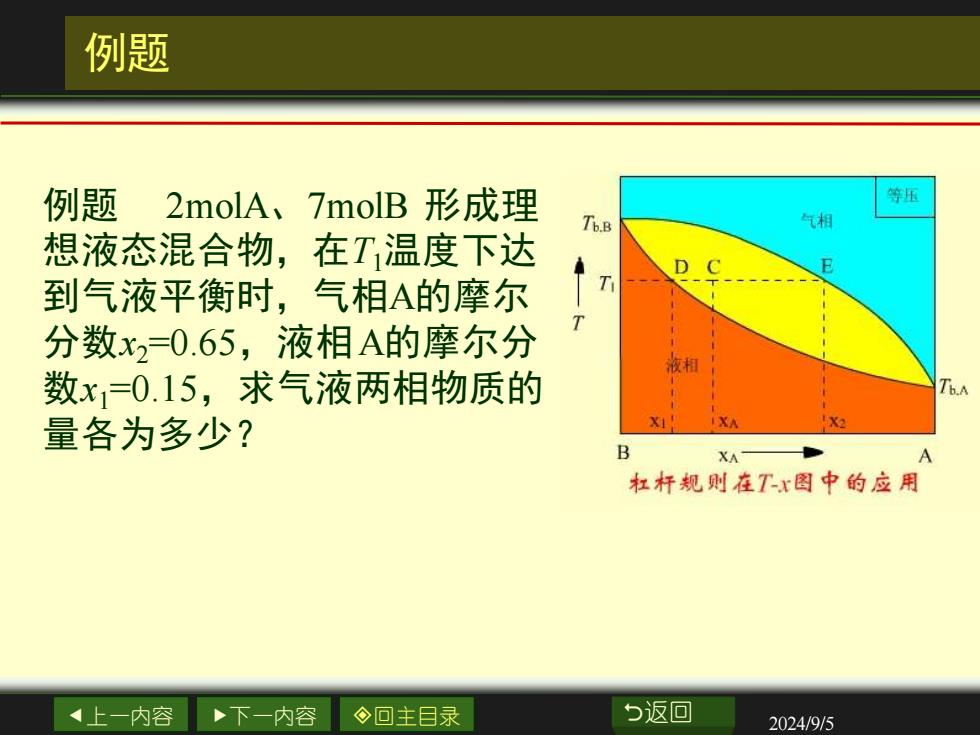
例题 例题 2molA、7molB形成理 等压 Tb.B 气相 想液态混合物,在T,温度下达 D 到气液平衡时,气相A的摩尔 T 分数x2=0.65,液相A的摩尔分 夜相 数x1=0.15,求气液两相物质的 量各为多少? X2 XA 杠杆规则在Tx图中的应用 上一内容 下一内容 ◇回主目录 与返回 2024/9/5
上一内容 下一内容 回主目录 返回 2024/9/5 例题 例题 2molA、7molB 形成理 想液态混合物,在T1温度下达 到气液平衡时,气相A的摩尔 分数x2=0.65,液相A的摩尔分 数x1=0.15,求气液两相物质的 量各为多少?
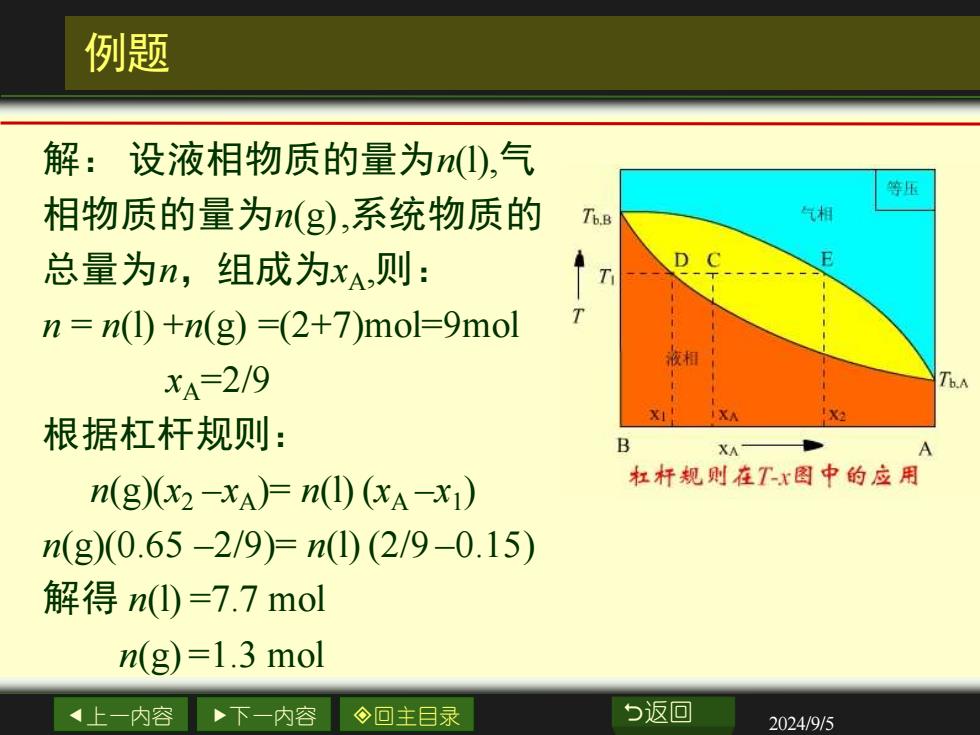
例题 解:设液相物质的量为①),气 等压 相物质的量为n(g),系统物质的 To.B 气相 总量为n,组成为xA,则: D C n=n()+n(g)-=(2+7)mol=9mol 夜相 xA=2/9 b.A XA 根据杠杆规则: XA n(g)(x2-xA)=n(1)(XA-x1) 杠杆规则在Tx图中的应用 (g(0.65-2/9)=n(①)(2/9-0.15) 解得n()=7.7mol n(g)=1.3 mol 4上一内容 下一内容 ◇回主目录 与返回 2024/9/5
上一内容 下一内容 回主目录 返回 2024/9/5 例题 解: 设液相物质的量为n(l),气 相物质的量为n(g),系统物质的 总量为n,组成为xA,则: n = n(l) +n(g) =(2+7)mol=9mol xA=2/9 根据杠杆规则: n(g)(x2 –xA)= n(l) (xA –x1 ) n(g)(0.65 –2/9)= n(l) (2/9 –0.15) 解得 n(l) =7.7 mol n(g) =1.3 mol