
信息检索与数据挖掘-论文阅读 Neural Ordinary Differential Equations 吴宁谦SA18006140
信息检索与数据挖掘-论文阅读 Neural Ordinary Differential Equations 吴宁谦 SA18006140

Neural Ordinary Differential Equations 摘要 选有NIPS Ricky T.Q.Chen",Yulia Rubanova*,Jesse Bettencourt*,David Duvenaud 2018 best paper University of Toronto,Vector Institute Toronto,Canada {rtqichen,rubanova,jessebett,duvenaud)Ocs.toronto.edu 论文介绍了一个新的深度神经网络家族NeuralODE。 它对神经网络的隐状态的导数进行参数化,使用微 分方程求解器计算网络的输出。这类模型只需要常 数级的内存成本,并且能在计算速度和模型精度之 间进行权衡。 论文在连续深度残差网络与连续时间隐变量模型上,进 行了验证实验。 论文提出了连续标准化流(CNF),它是一种通过最大似然 进行训练的生成模型。 论文展示了如何通过ODE求解器进行可扩展的反向传播, 允许大规模模型中的端到端训练
摘要 论文介绍了一个新的深度神经网络家族NeuralODE。 它对神经网络的隐状态的导数进行参数化,使用微 分方程求解器计算网络的输出。这类模型只需要常 数级的内存成本,并且能在计算速度和模型精度之 间进行权衡。 论文在连续深度残差网络与连续时间隐变量模型上,进 行了验证实验。 论文提出了连续标准化流(CNF),它是一种通过最大似然 进行训练的生成模型。 论文展示了如何通过ODE求解器进行可扩展的反向传播, 允许大规模模型中的端到端训练。 选自NIPS 2018 best paper

介绍-基本思想 诸如残差网络,递归神经网络(RNN),或标准化 流等神经网络构架中一般会含有重复的层块来 有序地保留信息。一般可以写成: ht+1 ht f(ht,0t) where t∈{0..T}and ht∈RD 这可以看成是一个微分方程的欧拉迭代求解。 当层数趋于无穷,△t趋于零时,上式可以化为: dh(t)=f(h(t),t.0) dt
介绍 – 基本思想 诸如残差网络,递归神经网络(RNN),或标准化 流等神经网络构架中一般会含有重复的层块来 有序地保留信息。一般可以写成: 这可以看成是一个微分方程的欧拉迭代求解。 当层数趋于无穷,Δt趋于零时,上式可以化为:
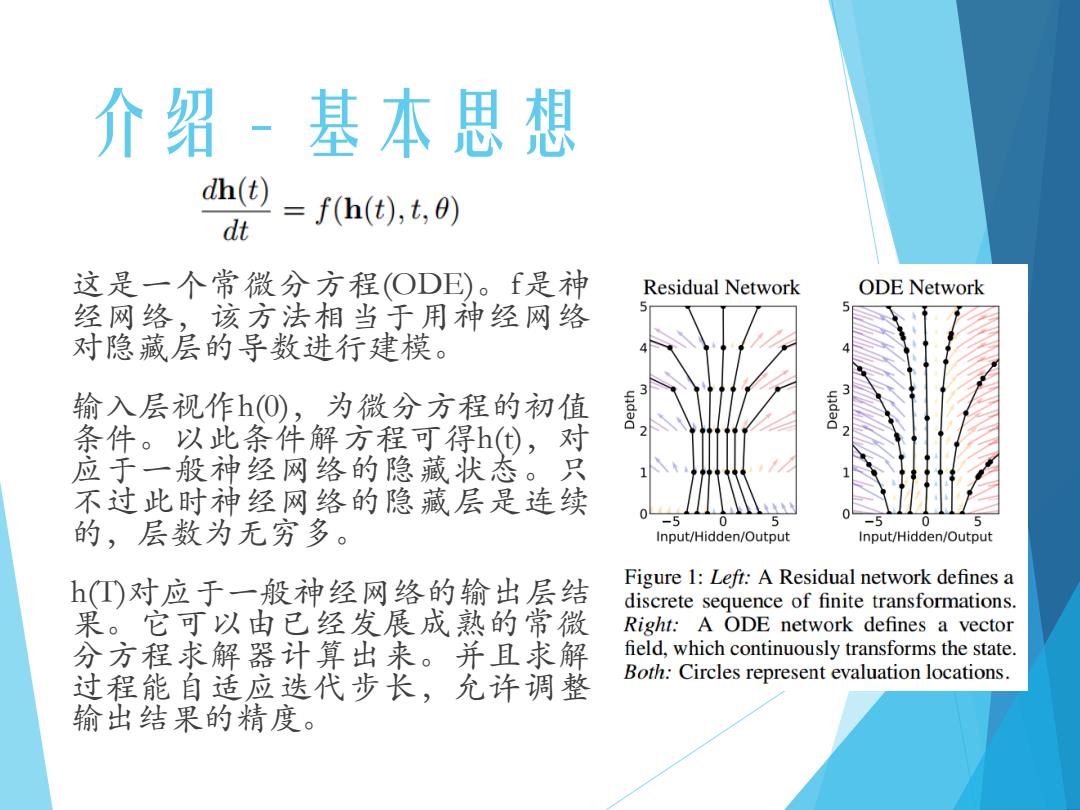
介绍-基本思想 dh(t) f(h(t),t,0) dt 这是一个常微分方程(ODE)。f是神 Residual Network ODE Network 经网络,该方法相当于用神经网络 对隐藏层的导数进行建模。 输入层视作h(O),为微分方程的初值 条件。以此条件解方程可得h(①,对 应于一般神经网络的隐藏状态。 不过此时神经网络的隐藏层是连续 -5 的,层数为无穷多。 Input/Hidden/Output Input/Hidden/Output h(T)对应于一般神经网络的输出层结 Figure 1:Left:A Residual network defines a discrete sequence of finite transformations. 果。它可以由已经发展成熟的常微 Right:A ODE network defines a vector 分方程求解器计算出来。并且求解 field,which continuously transforms the state 过程能自适应迭代步长,允许调整 Both:Circles represent evaluation locations. 输出结果的精度
介绍 – 基本思想 这是一个常微分方程(ODE)。f是神 经网络,该方法相当于用神经网络 对隐藏层的导数进行建模。 输入层视作h(0),为微分方程的初值 条件。以此条件解方程可得h(t),对 应于一般神经网络的隐藏状态。只 不过此时神经网络的隐藏层是连续 的,层数为无穷多。 h(T)对应于一般神经网络的输出层结 果。它可以由已经发展成熟的常微 分方程求解器计算出来。并且求解 过程能自适应迭代步长,允许调整 输出结果的精度

介绍-ODE的优点 内存效率高。不需要存储任何中间变量,内存空间 复杂度为○(1)。 允许自适应计算。现代ODE求解器已经发展了120 余年,现在的求解器可以在运行中调整其评估策略 以达到所要求的精度水平。 参数效率高。在相同的性能下比传统的神经网络所 需参数更少。 可扩展和可逆。结合标准化流与ODE,可以让计 算更容易,突破了标准化流的性能瓶颈。 更灵活。ODE连续时间序列模型,允许接入任意 时间点的训练数据,无需固定的采样间隔,能解决 更复杂的问题
介绍 – ODE的优点 内存效率高。不需要存储任何中间变量,内存空间 复杂度为O(1)。 允许自适应计算。现代ODE求解器已经发展了120 余年,现在的求解器可以在运行中调整其评估策略 以达到所要求的精度水平。 参数效率高。在相同的性能下比传统的神经网络所 需参数更少。 可扩展和可逆。结合标准化流与ODE,可以让计 算更容易,突破了标准化流的性能瓶颈。 更灵活。ODE连续时间序列模型,允许接入任意 时间点的训练数据,无需固定的采样间隔,能解决 更复杂的问题