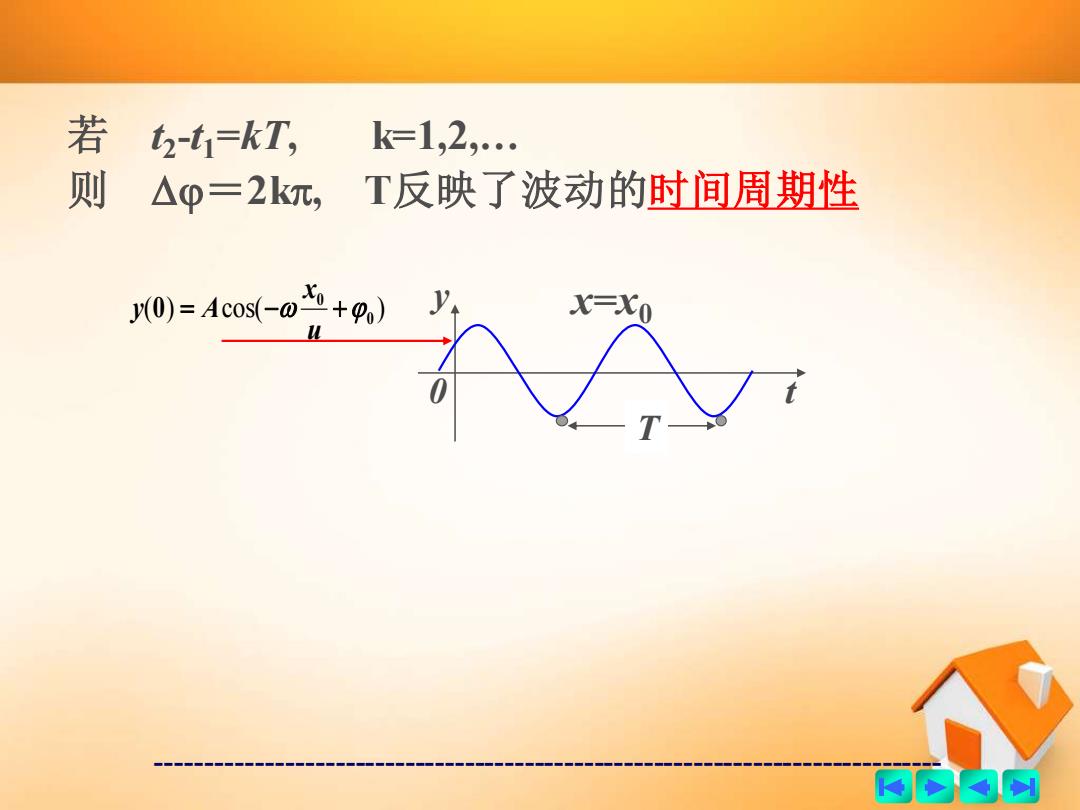
若 2-t1=kT, k=1,2,… 则 △p=2k阢,T反映了波动的时间周期性 0)=Ac0s-o+m,) x-x0 商的内网
------------------------------------------------------------------------------- 若 t2 -t1=kT, k=1,2,… 则 =2k, T反映了波动的时间周期性 T 0 t y ( ) cos( ) 0 0 0 = − + u x y A x=x0

2.如果给定t,即=t0 y=Acosl@(t-x)+gol=Acos(-@+a+o) X y=Acos(@*+) p=-0t。-p0 y化,)→y)→,时刻空间各点位移分布 商的内网
------------------------------------------------------------------------------- 2. 如果给定t,即t=t0 cos[ ( ) ] = 0 − +0 u x y A t cos( ) = − + 0 +0 t u x A cos( ) / = + u x y A = − 0 −0 t / y(x,t) → y(x) → t0 时刻空间各点位移分布
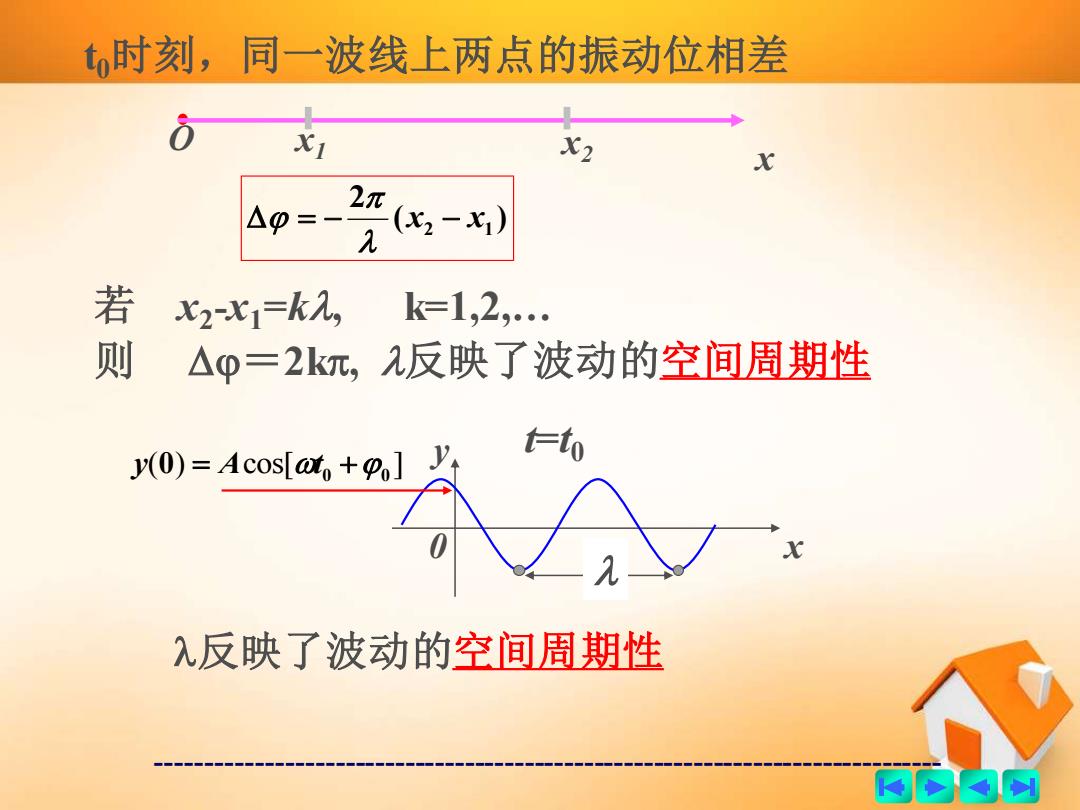
时刻,同一波线上两点的振动位相差 X1 X2 X 2 △=- 2(x2-) 若 2-X1=k2, k=1,2,… 则 △p=2km,入反映了波动的空间周期性 y(0)=Acos[at+] o λ反映了波动的空间周期性 商的内网
------------------------------------------------------------------------------- t0时刻,同一波线上两点的振动位相差 x O x2 x1 ( ) 2 = − x2 − x1 若 x2 -x1=k, k=1,2,… 则 =2k, 反映了波动的空间周期性 0 x y ( ) cos[ ] 0 = 0 +0 y A t t=t0 反映了波动的空间周期性
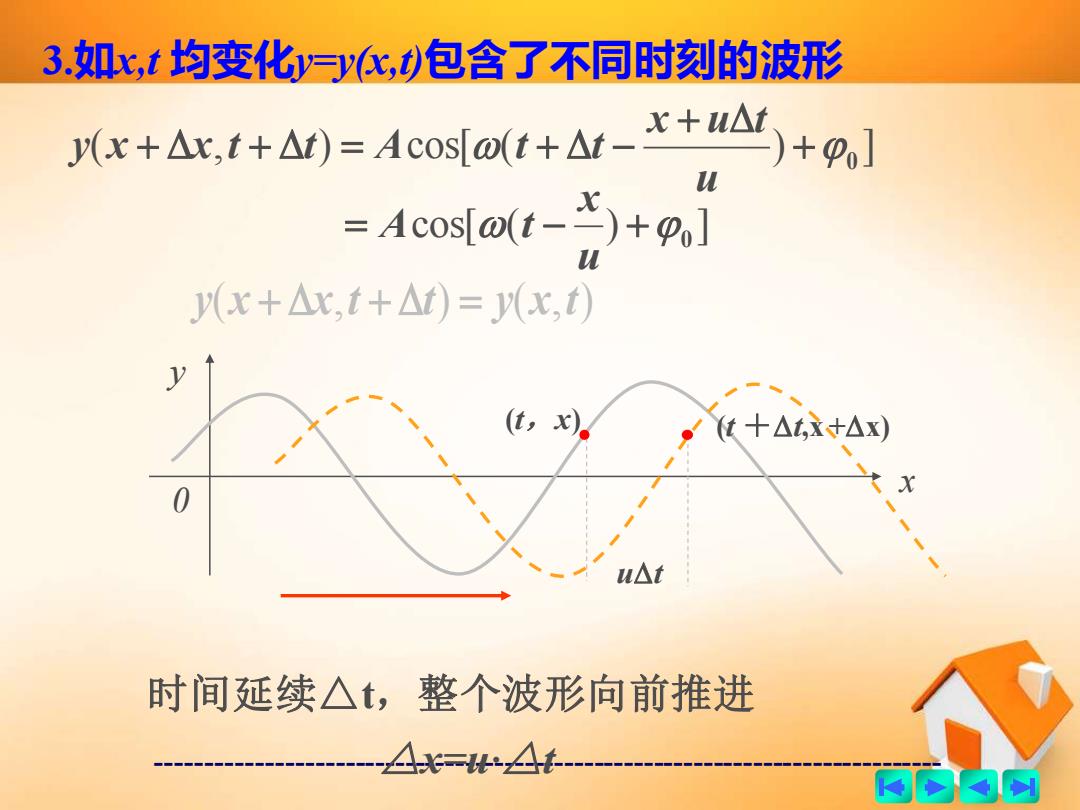
3如x,t均变化y化,)包含了不同时刻的波形 川x+Ax,t+△)=cosf[ot+af-x+A+m,] =Acos[@(t-X)+o] 儿 x+△x,t+△t)=Jy(x,t) (t, x 使十△,这+△x) X u△t 时间延续△t,整个波形向前推进 △比=W44 两的肉例
------------------------------------------------------------------------------- 3.如x,t 均变化y=y(x,t)包含了不同时刻的波形 ( , ) cos[ ( ) ] +0 + + + = + − u x u t y x x t t A t t cos[ ( ) ] = − +0 u x A t y(x + x,t + t) = y(x,t) 0 y x ut (t +t,x +x) (t,x) 时间延续△t,整个波形向前推进 △x=u·△t