
University of Electronic Science and Technology of China 1.平板光波导的几何光学分析 1956 有效折射率 利用有效折射率可将平板波导的色散方程写为: k,hd-N)=m元+aretan( N2- -N2 +arctan( (TE) (2-23) N2- 2 khVm-N2)=mπ+arctan( arctan( N) 居VR-N2 (TM)(2-24) 26
University of Electronic Science and Technology of China 26 ➢ 有效折射率 (2-23) (2-24) 利用有效折射率可将平板波导的色散方程写为: ( ) arctan( ) 2 2 1 2 2 2 2 2 0 1 n N N n k h n N m − − − = + arctan( ) (TE) 2 2 1 2 3 2 n N N n − − + ( ) arctan( ) 2 2 1 2 2 2 2 2 2 2 2 1 0 1 n N N n n n k h n N m − − − = + arctan( ) (TM) 2 2 1 2 3 2 2 3 2 1 n N N n n n − − + 1. 平板光波导的几何光学分析

University of Electronic Science and Technology of China 1.平板光波导的几何光学分析 1956 基本结论 平板波导的色散方程中,取值的离散性说明平板波导中 光波的模式(表现为传播常数B或有效折射率川): 不是连续的,而是一系列确定的分立值。 2) 可以表示为TEm(横电)或TMm(横磁)。 3) m取不同的值时对应不同的模式,不同的模式具有不 同的模角(传播路径特征),并且它们之间是不相干的, 或者说是独立传播的。 =0的模称为基模,基模以上依次称为一阶模,二阶 模…。 5) 对给定的材料,芯层越薄,越小。当波导厚度薄到仅 基模可以传播时,该波导称为单模波导。 27
University of Electronic Science and Technology of China 27 ➢ 基本结论 平板波导的色散方程中,m取值的离散性说明平板波导中 光波的模式 (表现为传播常数 或有效折射率N ): 1) 不是连续的,而是一系列确定的分立值。 2) 可以表示为TEm(横电)或TMm (横磁)。 3) m取不同的值时对应不同的模式,不同的模式具有不 同的模角(传播路径特征),并且它们之间是不相干的, 或者说是独立传播的。 1. 平板光波导的几何光学分析 4) m=0的模称为基模,基模以上依次称为一阶模,二阶 模……。 5) 对给定的材料,芯层越薄,m越小。当波导厚度薄到仅 基模可以传播时,该波导称为单模波导
University of Electronic Science and Technology of China X 2.平板光波导的电磁理论 1956 定性解释 图2-11.平板波导及坐标系 侧视图 截面图 n3 n3 ni ni n2 n2 基底 基底 假设波导材料为均匀、各向同性、无源、无损的非磁性 介质(4=1h),同时假设上、下包层厚度无限大,波 导在y,z方向无限延伸。一般的平板波导可以认为是满 足以上条件的。 28
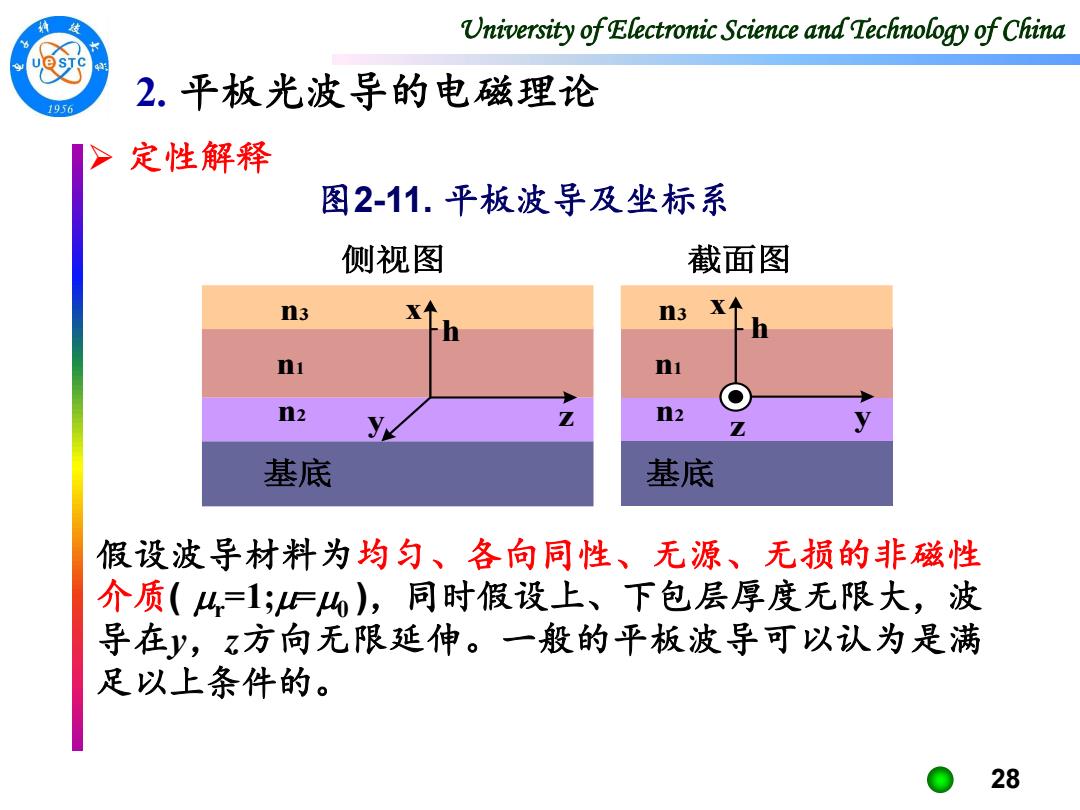
University of Electronic Science and Technology of China 28 ➢ 定性解释 图2-11. 平板波导及坐标系 假设波导材料为均匀、各向同性、无源、无损的非磁性 介质( r =1;=0 ),同时假设上、下包层厚度无限大,波 导在y,z方向无限延伸。一般的平板波导可以认为是满 足以上条件的。 基底 n1 n2 n3 基底 n1 n2 x n3 y z z x y 侧视图 截面图 h h 2. 平板光波导的电磁理论

University of Electronic Science and Technology of China 2.平板光波导的电磁理论 1956 > 定性解释 波导内传输的场应满足亥姆霍滋方程: V2E+kon2E=0 (2-25) V2H+kin2H=0 (2-26) 设波为沿z方向传播的简谐波,则上式的解为: E(r,t)=E(x,y)expli(@t-Bz)] (2-27) H(r,t)=H(x,y)expli(at-B)] (2-28) ∂2 根据以上两式,显然有 22→B2 (2-29) 29
University of Electronic Science and Technology of China 29 ➢ 定性解释 波导内传输的场应满足亥姆霍兹方程: 0 2 2 0 2 E + k ni E = 0 2 2 0 2 H + k ni H = 设波为沿z方向传播的简谐波,则上式的解为: E(r,t) = E(x, y)exp[i(t − z)] H(r,t) = H(x, y)exp[i(t − z)] (2-27) (2-25) (2-26) (2-28) 根据以上两式,显然有 2 2 2 → − z (2-29) 2. 平板光波导的电磁理论

University of Electronic Science and Technology of China X 2.平板光波导的电磁理论 1956 > 定性解释 由于波导在y方向一致均匀,因此 ∂ →0 (2-30) 从而有:E(x,y)=E:(x)=Ex(x)e+E,(x)°(2-31) 从而对电场分量有: C2E,(e)+(m-B2)E,()=0(2 -32) 30
University of Electronic Science and Technology of China 30 ➢ 定性解释 由于波导在y方向一致均匀,因此 → 0 y 从而对电场分量有: ( ) ( ) ( ) 0 2 2 2 2 0 2 + − = E x k n E x x i i i (2-32) (2-30) 从而有: E x y E x E x x E x y i i x y ( , ) = ( ) = ( ) ˆ + ( )ˆ (2-31) 2. 平板光波导的电磁理论