微观粒子的波动性与粒子行为的统 计性规律联系在一起,表现为: 无机化学电子款 微观粒子的波动性是大量微粒运动 表现出来的性质,即是具有统计意义的 概率波
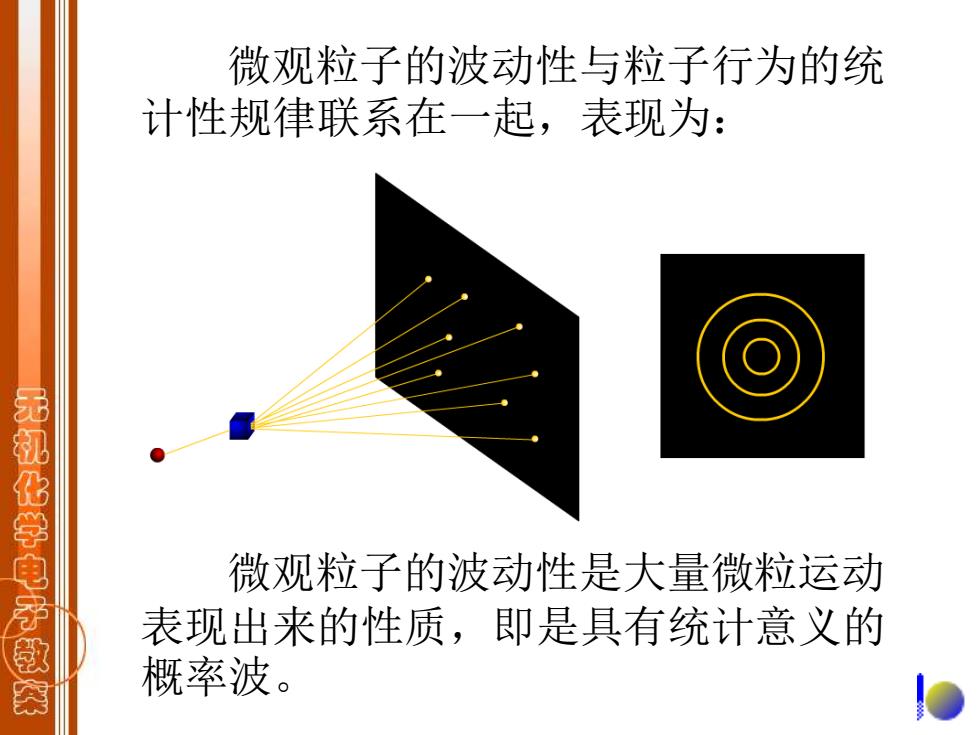
微观粒子的波动性与粒子行为的统 计性规律联系在一起,表现为: 微观粒子的波动性是大量微粒运动 表现出来的性质,即是具有统计意义的 概率波

§83氨原子结构的量子力学描述 8.3.1 Schrodinger?方程与波函数 8.3.2 量子数 3>8.3.3 概率密度与电子云 8.3.4原子轨道与电子云 的空间图像 返回
8.3.2 量子数 §8.3 氢原子结构的量子力学描述 8.3.3 概率密度与电子云 8.3.4 原子轨道与电子云 的空间图像 8.3.1 Schro ••dinger方程与波函数

8.3.1 Schrodinger方程与波函数 十 8x2 () w:波函数 E:能量 无机化学电子款 :势能 m: 质量 h:Planck常数 x,y,z:空间直角坐标
( ) 8π 2 2 2 2 2 2 2 2 E V h m x y z = − − + + x, y,z:空间直角坐标 h:Planck常数 V:势能 E:能量 :波函数 m:质量 8.3.1 Schro ••dinger方程与波函数

坐标变换 球坐标(,0,p)与直角坐标系的关系 z =rcose y=rsinsin) x=rsincos) 无机化学电子教突 r=vx2+y+z 0:0≈2元 Ψ(r,8,0)=R(rY(8,0) 0:0~元
球坐标(r,θ,φ)与直角坐标系的关系 2 2 2 r = x + y + z z = r cosq y = rsinq sin x = rsinq cos (r,θ,φ) = R(r)·Y(θ,φ) 0~2π 0~ π q : : 坐标变换

8.3.2量子数 l.主量子数n n=1,2,3,4,5,6.正整数 对应K,L,MN,O,P.电子层 与电子能量有关,对于氢原子而言, 电子能量唯一决定于n。 无机化学电子款 2.179×10-18 E- J 22 n愈大,电子离核平均距离愈远, 能量愈高
1. 主量子数 n n =1, 2, 3, 4, 5, 6. 正整数 8.3.2 量子数 对应 K, L, M, N, O, P. 电子层 •与电子能量有关,对于氢原子而言, 电子能量唯一决定于n。 J 2.179 10 2 1 8 n E − = − •n愈大,电子离核平均距离愈远, 能量愈高