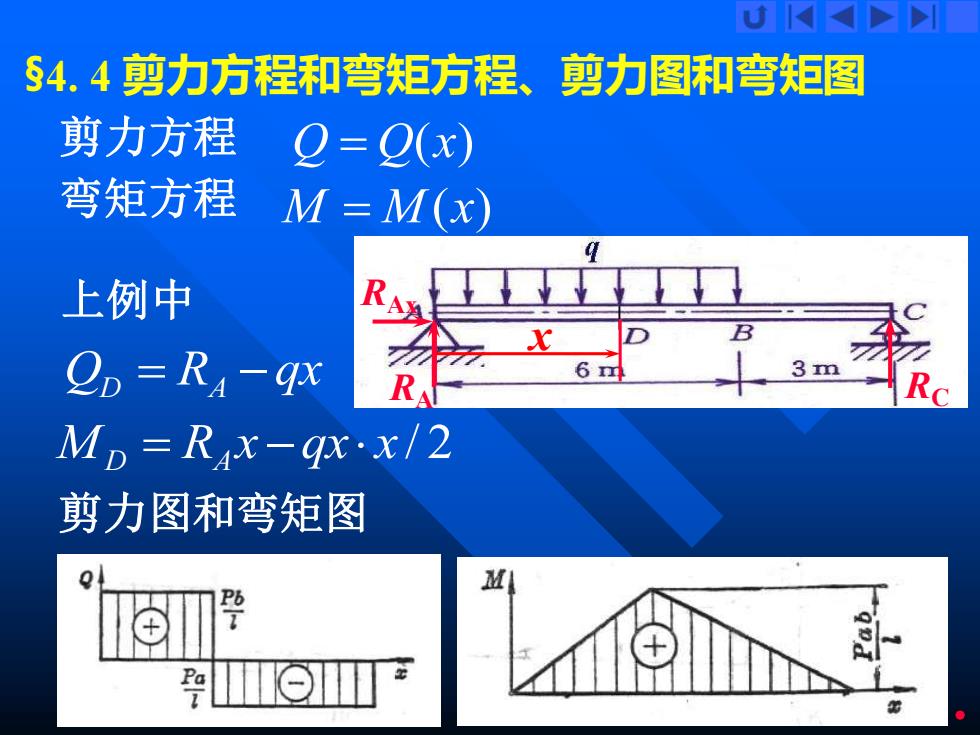
U K §4.4剪力方程和弯矩方程、剪力图和弯矩图 剪力方程 2=0(x) 弯矩方程 M=M(x) 上例中 Op=RA-9x 61 3m RA Mp=Rx-gx.x/2 剪力图和弯矩图 Pa
17 §4. 4 剪力方程和弯矩方程、剪力图和弯矩图 剪力方程 x RA RAx RC Q = Q(x) 弯矩方程 M = M (x) MD = RA x −qx x / 2 Q R qx D = A − 上例中 剪力图和弯矩图
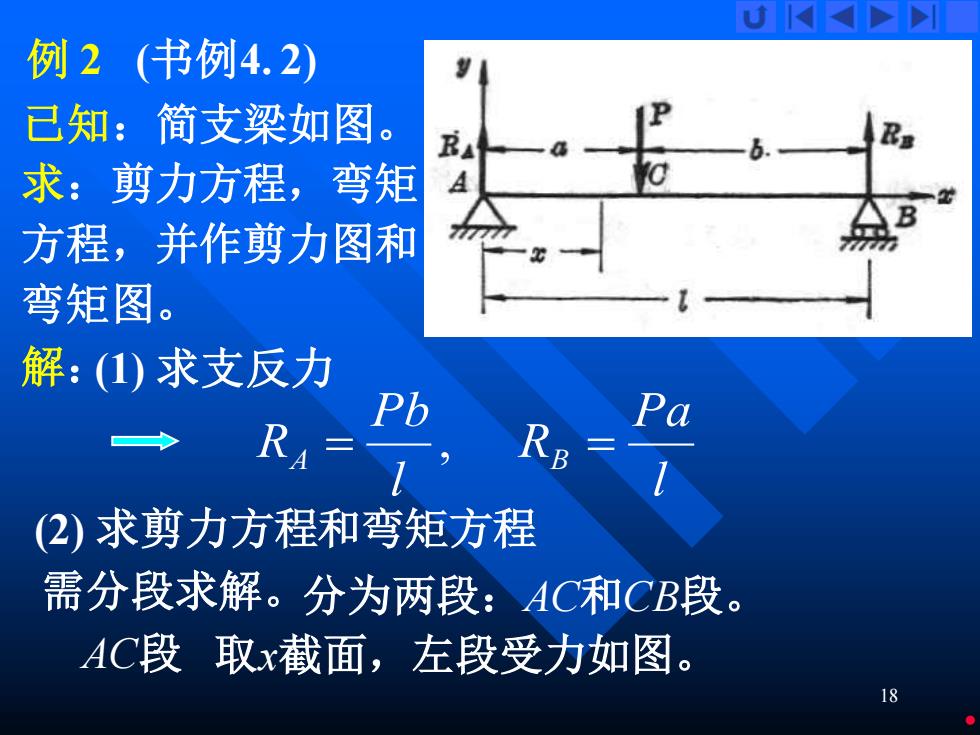
U K 例2(书例4.2) 已知:简支梁如图。 求:剪力方程,弯矩 A 方程,并作剪力图和 弯矩图。 解:(1)求支反力 >h Pa RA RB (2)求剪力方程和弯矩方程 需分段求解。分为两段:AC和CB段。 AC段取x截面,左段受力如图。 18
18 例 2 (书例4. 2) 已知:简支梁如图。 解: 求:剪力方程,弯矩 方程,并作剪力图和 弯矩图。 (1) 求支反力 , l Pb RA = 需分段求解。 l Pa RB = (2) 求剪力方程和弯矩方程 分为两段:AC和CB段。 AC段 取x截面,左段受力如图
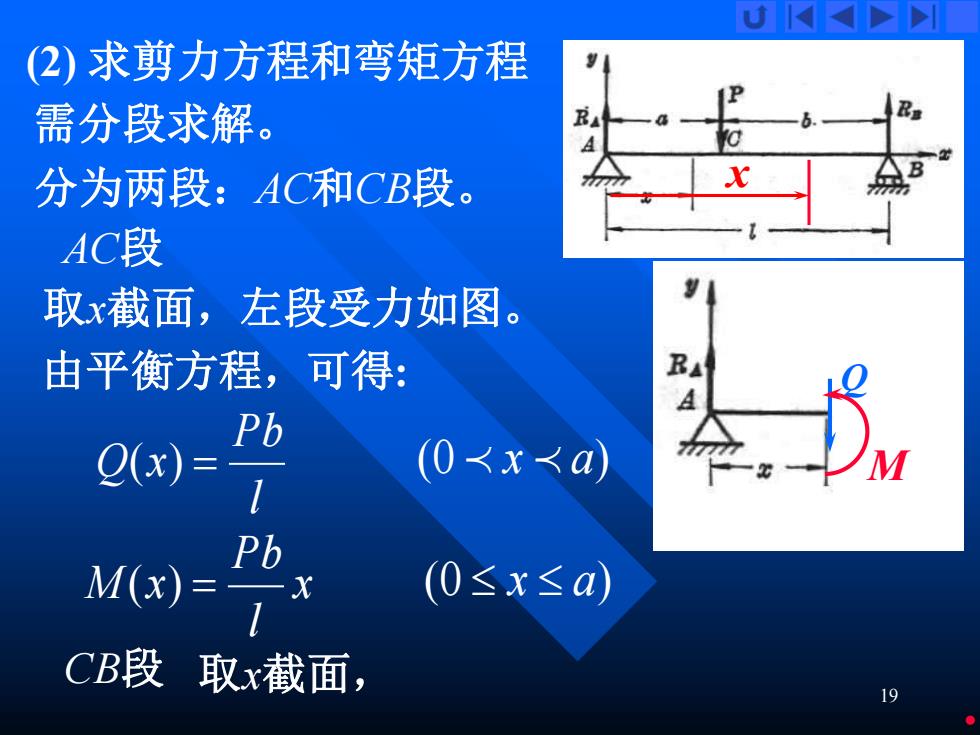
U (2)求剪力方程和弯矩方程 需分段求解。 分为两段:AC和CB段。 AC段 取x截面,左段受力如图。 由平衡方程,可得: Pb Q(x)= (03xRa) 1 Pb M(x) (0≤x≤a) CB段] 取x截面, 19
19 需分段求解。 l Pb Q(x) = (2) 求剪力方程和弯矩方程 分为两段:AC和CB段。 AC段 取x截面,左段受力如图。 Q M 由平衡方程,可得: (0 x a) x l Pb M (x) = (0 x a) CB段 x 取x截面
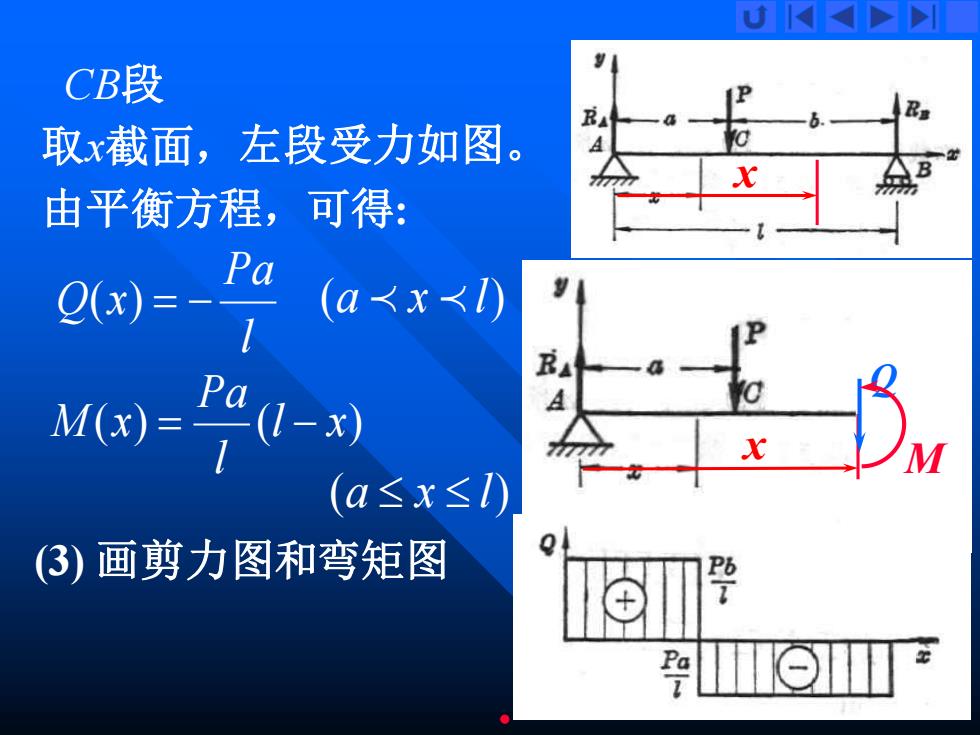
U K CB段 取x截面,左段受力如图。 A 由平衡方程,可得: 0(x)=-7 (a<x<) P M (a≤x≤) 3)画剪力图和弯矩图 Pa
20 l Pa Q(x) = − 由平衡方程,可得: (a x l) ( ) (l x) l Pa M x = − (a x l) CB段 x 取x截面, x Q M 左段受力如图。 (3) 画剪力图和弯矩图
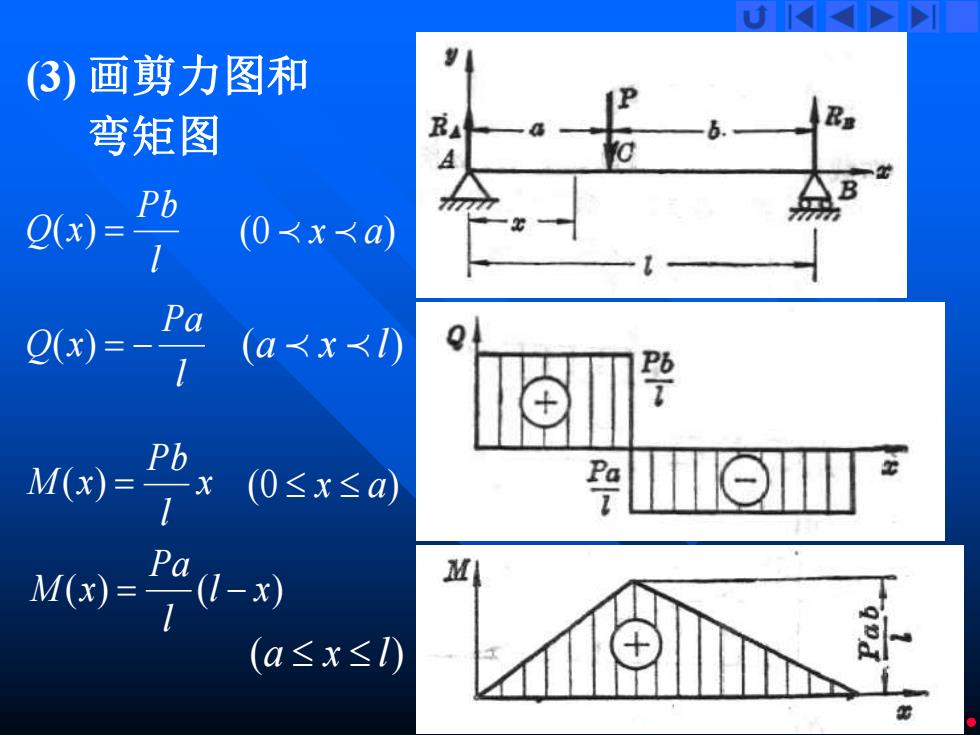
(3)画剪力图和 弯矩图 0c)= Pb (0<x人a Q=- a (a<x<1) Pb M(x)= (0sx≤a Pa M (a≤x≤
21 (3) 画剪力图和 弯矩图 l Pb Q(x) = (0 x a) x l Pb M (x) = (0 x a) l Pa Q(x) = − (a x l) ( ) (l x) l Pa M x = − (a x l)