S4.3剪力和弯矩 下面求解梁弯曲时的内力。 例子 已知:q=20 kN/m,尺寸 61 3m R 如图。 求:D截面处的内力。 解:求内力的方法 截面法。建立x坐标如图。 ()求支座反力 取整体,受力如图。 ∑X=0 Ri =0
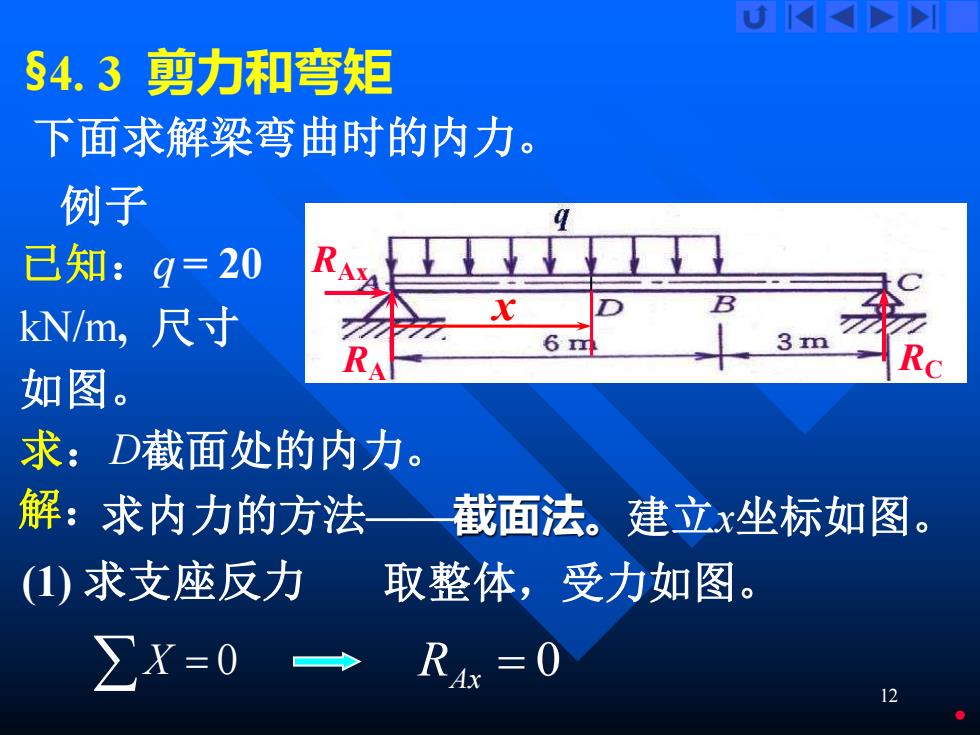
12 §4. 3 剪力和弯矩 下面求解梁弯曲时的内力。 例子 已知:q = 20 kN/m, 尺寸 如图。 求:D截面处的内力。 x 解:求内力的方法——截面法。建立x坐标如图。 (1) 求支座反力 RA RAx RC 取整体,受力如图。 X = 0 RAx = 0

U 61 3 (1)求支座反力 取整体,受力如图。 ∑X=0 =0 ∑M(F)=0 R=80kN ∑Y=0 Rc 40 kN (2)求D截面内力 从D处截开,取左段。 横截面上的内力如图
13 (1) 求支座反力 取整体,受力如图。 X = 0 RAx = 0 x RA RC RAx (F) = 0 MC RA = 80 kN Y = 0 RC = 40 kN (2) 求D截面内力 从D处截开,取左段。 x RA QD 横截面上的内力如图。 RAx N MD
(2)求D截面内力 从D处截开,取左段。 横截面上的内力如图。 MD R ∑X=0 N=-R4x=0 ∑Y=0 2D=R4-9X=80-20x ∑M(F)=0 MD=R4x-9X·x/2 =80x-10x2 规律 Q=截面一侧所有横向外力代数和 M=截面一侧所有外力对截面形心力矩的代数和 14
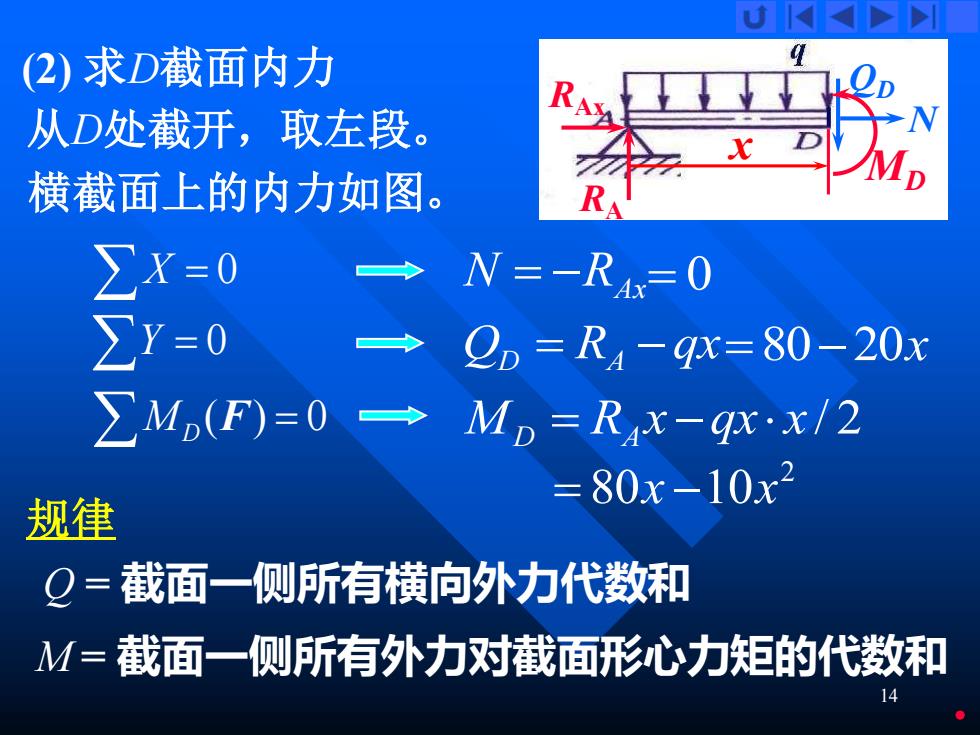
14 X = 0 N = −RAx (F) = 0 MD MD = RA x −qx x / 2 Y = 0 Q R qx D = A − (2) 求D截面内力 从D处截开,取左段。 横截面上的内力如图。 = 0 x RA QD MD N RAx = 80−20x 2 = 80x −10x 规律 Q = 截面一侧所有横向外力代数和 M = 截面一侧所有外力对截面形心力矩的代数和
3m R 若从D处截开,取右段。 横截面上的内力如图。 M Mp R 计算可得QD,M,的数值与取左段所得结果相同。 但从图上看,它们的方向相反。 剪力和弯矩的正负号规则如何?
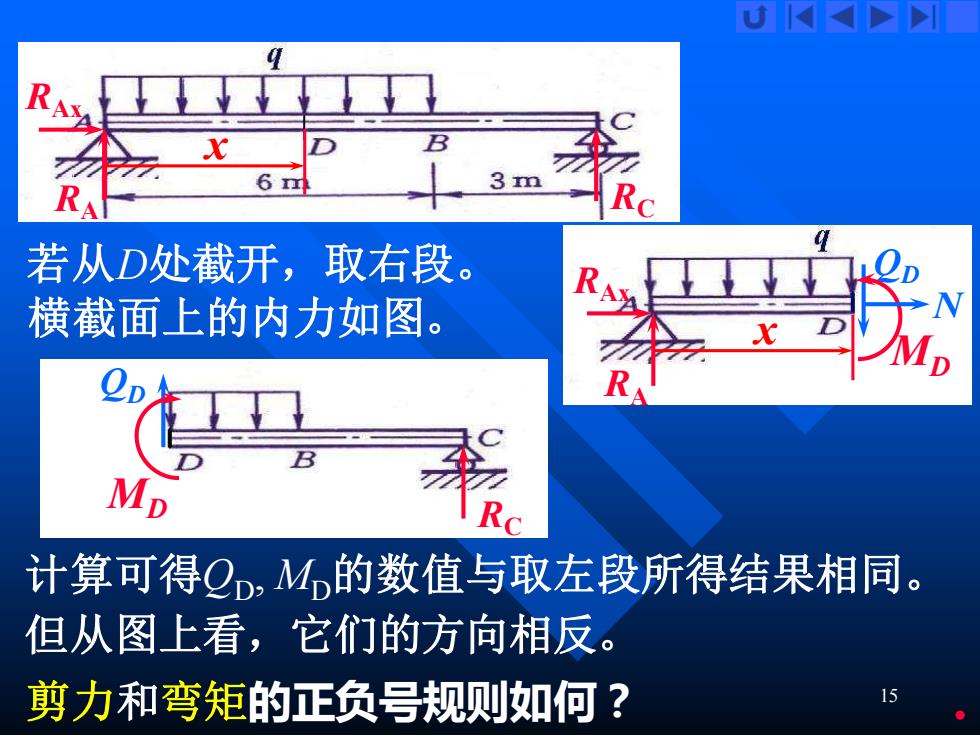
15 x RA RC RAx 若从D处截开,取右段。 横截面上的内力如图。 x RA QD MD N RAx RC QD MD 计算可得QD, MD的数值与取左段所得结果相同。 但从图上看,它们的方向相反。 剪力和弯矩的正负号规则如何?
U K 剪力和弯矩的正负号规定 剪力 使其作用的一 段梁产生顺时 针转动的剪力 为正。 弯矩 使梁产生上凹 M M (下凸)变形的 弯矩为正
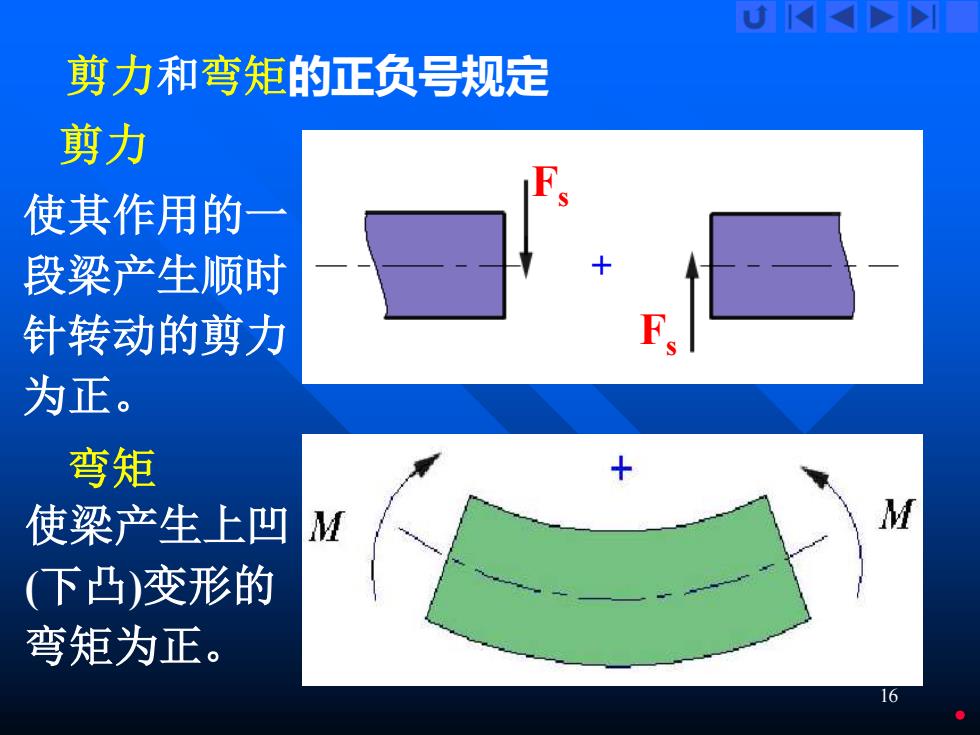
16 剪力 和弯矩的正负号规定F s F s 剪力 使其作用的一 段梁产生顺时 针转动的剪力 为正。 弯矩 使梁产生上凹 (下凸)变形的 弯矩为正