
If a o plane contains the principle axis and bisects the angle between two adjacent 2-fold axes then it is labeled od(Dihedral mirror planes 。Example:BFg Has a C3 principle axis Has three-C2 axes. Has three od planes (? C2 Example:H,C=C=CH, Od
If a σ plane contains the principle axis and bisects the angle between two adjacent 2-fold axes then it is labeled σd.(Dihedral mirror planes ) • Example: BF3 – Has a C3 principle axis – Has three-C2 axes. – Has three σd planes (?). σv Example: H2C=C=CH2 C2 C2 σd σd

5)The improper rotation axis a.n-fold rotation reflection,Rotary-reflection axis (S) Rotate 360/n followed by reflection in mirror plane perpendicular to axis of rotation Axis bisects the H-C-H bond angle Reflect through a plane that is perpendicular Rotate through to the original 90 rotation axis Example:H3C-CH; 56 The staggered form of ethane has an S axis composed of a 60 rotation followed by a reflection
Rotate 360°/n followed by reflection in mirror plane perpendicular to axis of rotation a. n-fold rotation + reflection, Rotary-reflection axis (Sn) 5) The improper rotation axis S4 The staggered form of ethane has an S6 axis composed of a 60° rotation followed by a reflection. S6 σh S6 Example: H3C-CH3
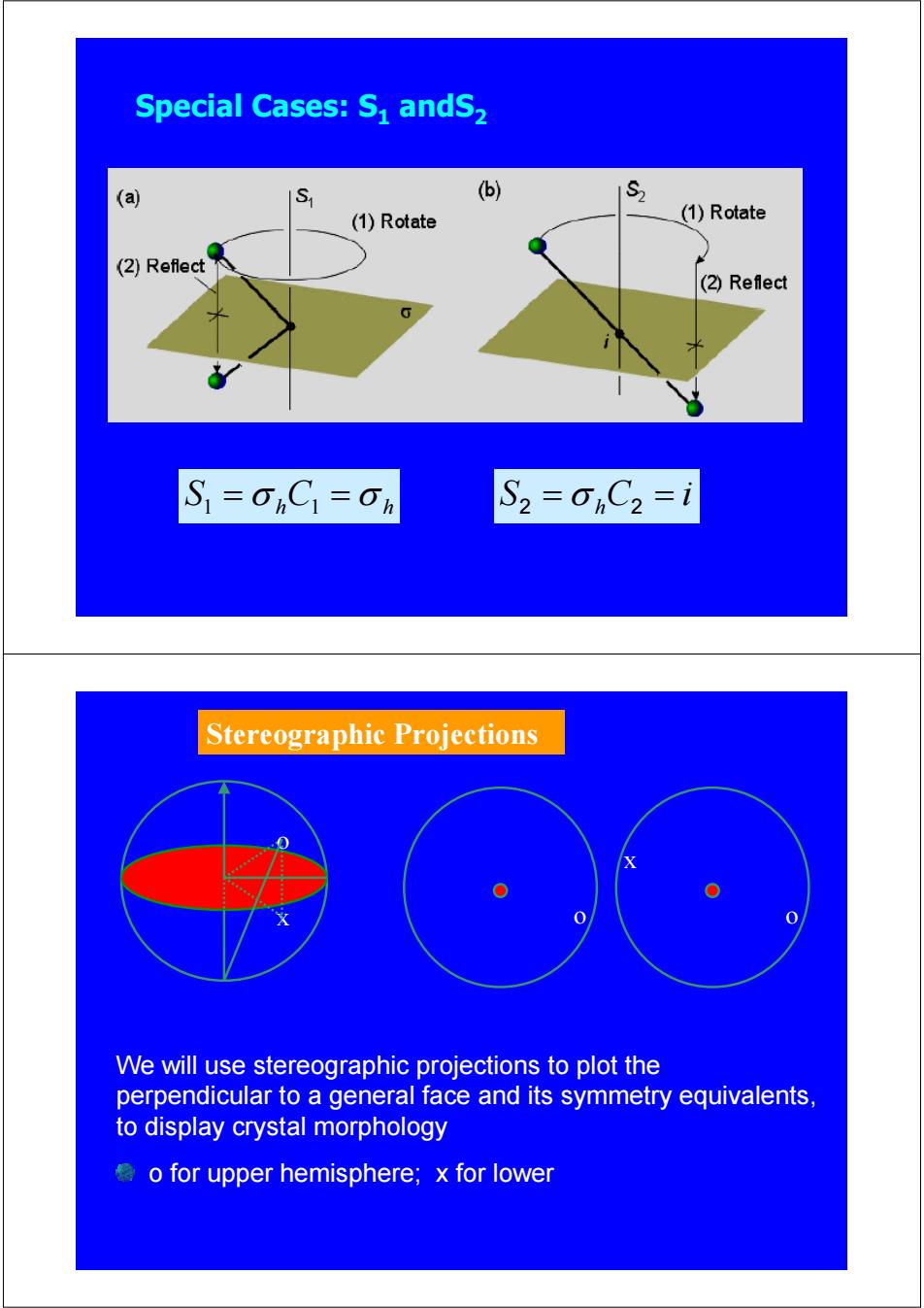
Special Cases:S andS, (a (6) S (1)Rotate (1)Rotate (2)Reflect (②Reflect S=OC=Oh S2=01C2=i Stereographic Projections 0 0 We will use stereographic projections to plot the perpendicular to a general face and its symmetry equivalents. to display crystal morphology o for upper hemisphere;x for lower
Special Cases: S1 andS2 S1 = σ hC1 = σ h S C i 2 = σ h 2 = Stereographic Projections o x o x We will use stereographic projections to plot the perpendicular to a general face and its symmetry equivalents, to display crystal morphology o for upper hemisphere; x for lower o

S3 S'=oC',S2=C32,S3=o,S4=C3,S5=oC32,S=E S3=OC3=C3+Om S4=oC41S42=C21,S43=oC4344=E S43 S5 =0C5=C5+O s=OCs:Ss2-Co2:Ss3=oCs:Ss-Cs:Sgs-0. =C6Sg7=oC2,S9=C3,S,9=oC61S10=E S6 =0C6
S3 = σ hC3 = C3 +σ h S = C S = C S = S = C S = C S = E 6 3 2 3 5 3 1 3 4 3 3 3 2 3 2 3 1 3 1 3 S σ ; ; σ; ; σ ; 3 4 C4 S =σ h S = C S = C S = C S = E 4 4 3 4 3 4 1 2 2 4 1 4 1 4 σ ; ; σ ; S C S C S C S C S E S C S C S C S C S = = = = = = = = = = 10 5 4 5 9 5 3 5 8 5 2 5 7 5 1 5 6 5 5 5 4 5 4 5 3 5 3 5 2 5 2 5 1 5 1 5 ; ; ; ; ; ; ; ; ; σ σ σ σ σ x S4 3 hC C h S5 =σ 5 = 5 +σ x S4 1 S4 2 S6 = σ hC6