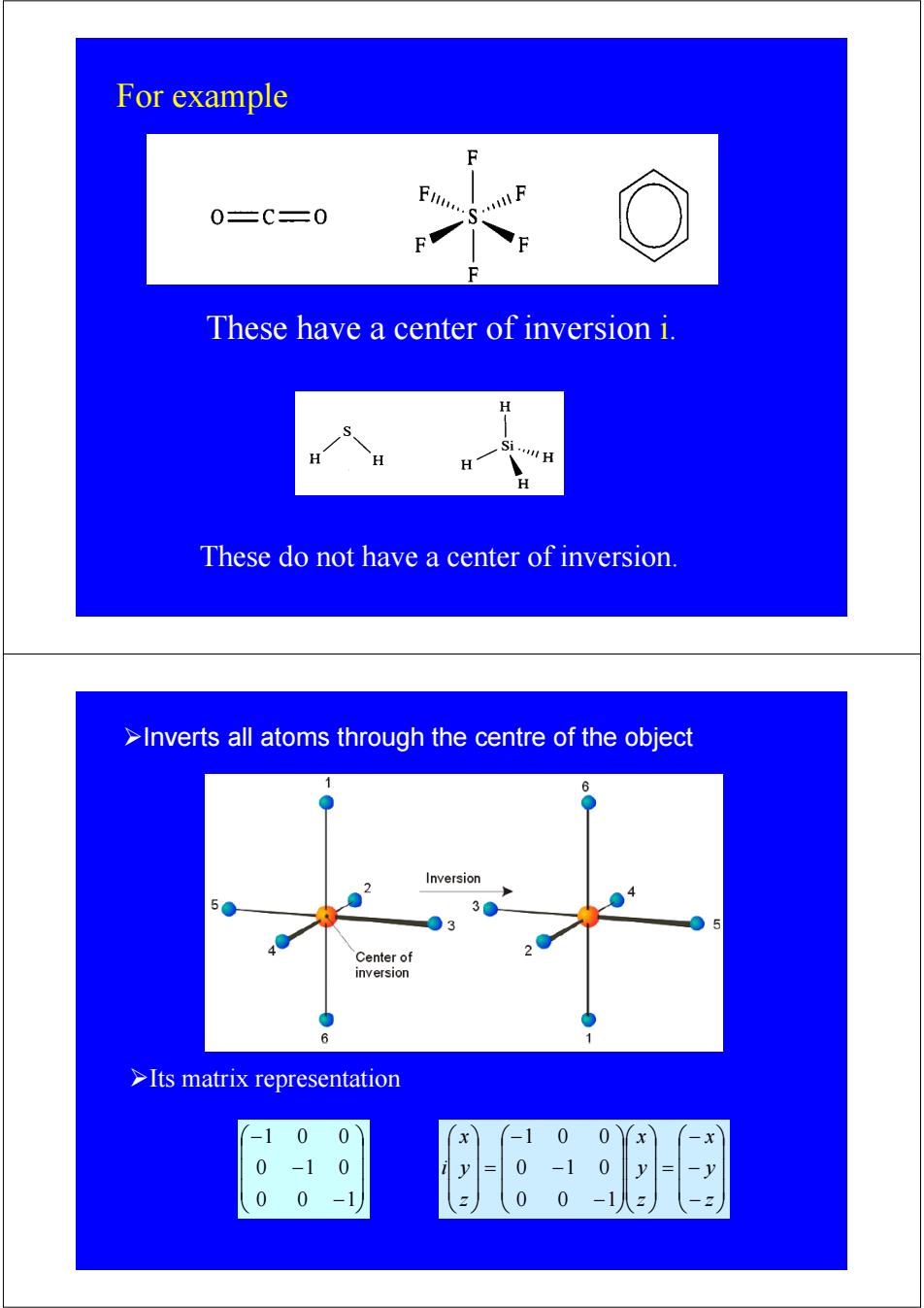
For example F 0=C=0 S. These have a center of inversion i. H H These do not have a center of inversion. >Inverts all atoms through the centre of the object 1 6 Inversion 5 30 03 Center of inversion 6 >Its matrix representation -1 0 0 0 0 -x 0 -1 0 0 -1 0 y 0 0 -1 0 0
These do not have a center of inversion. These have a center of inversion i. For example ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − − 0 0 1 0 1 0 1 0 0 ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − − = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − − = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ z y x z y x z y x i 0 0 1 0 1 0 1 0 0 ¾Its matrix representation ¾Inverts all atoms through the centre of the object
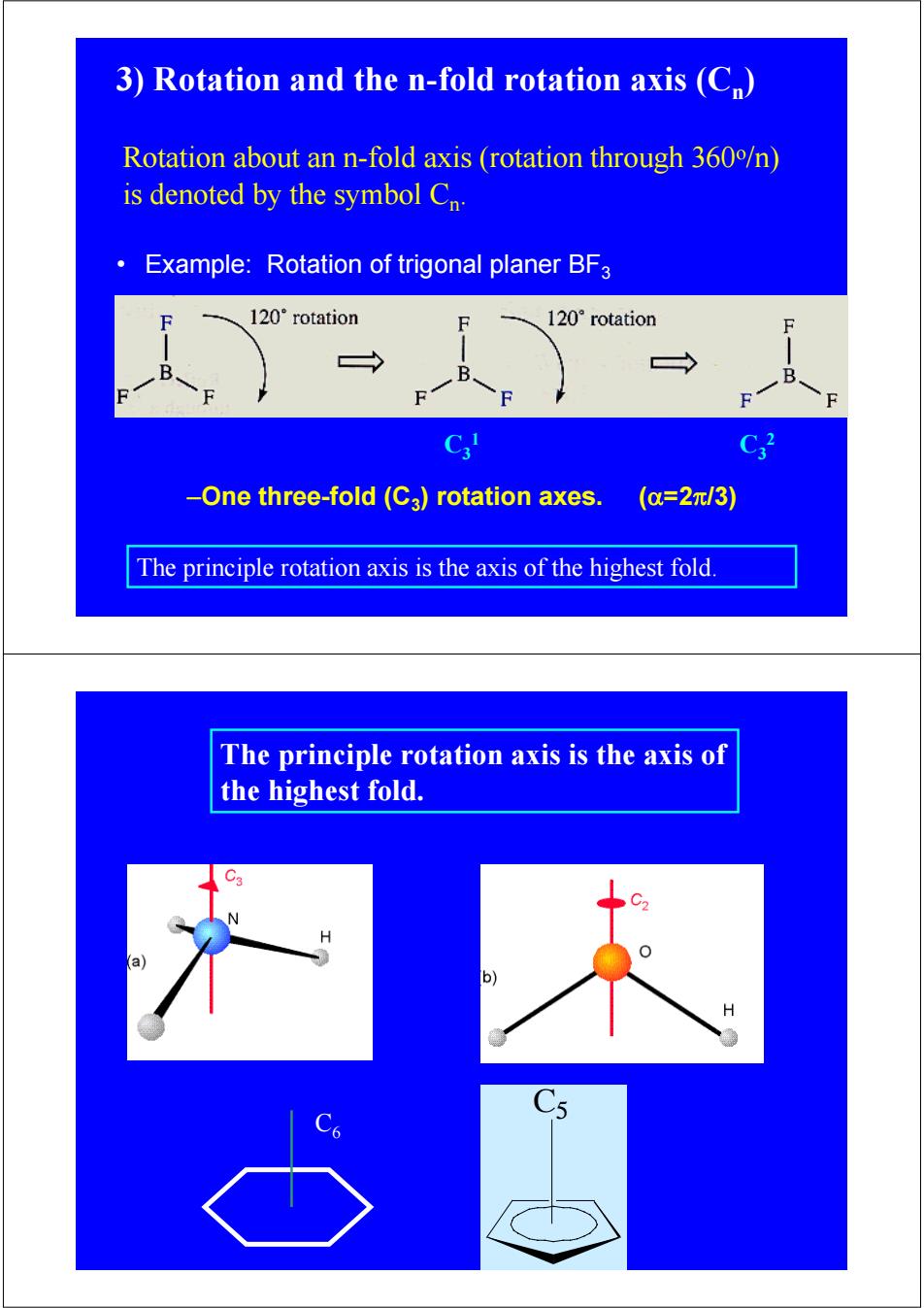
3)Rotation and the n-fold rotation axis(C) Rotation about an n-fold axis (rotation through 360/n) is denoted by the symbol Cn. Example:Rotation of trigonal planer BFa 120°rotation 120°rotation F → B C3 -One three-fold(C3)rotation axes. (a=2元/3) The principle rotation axis is the axis of the highest fold The principle rotation axis is the axis of the highest fold. H
• Example: Rotation of trigonal planer BF3 C3 1 C3 2 Rotation about an n-fold axis (rotation through 360o/n) is denoted by the symbol Cn. 3) Rotation and the n-fold rotation axis (Cn) The principle rotation axis is the axis of the highest fold. –One three-fold (C3) rotation axes. (α=2π/3) C5 The principle rotation axis is the axis of the highest fold. C6
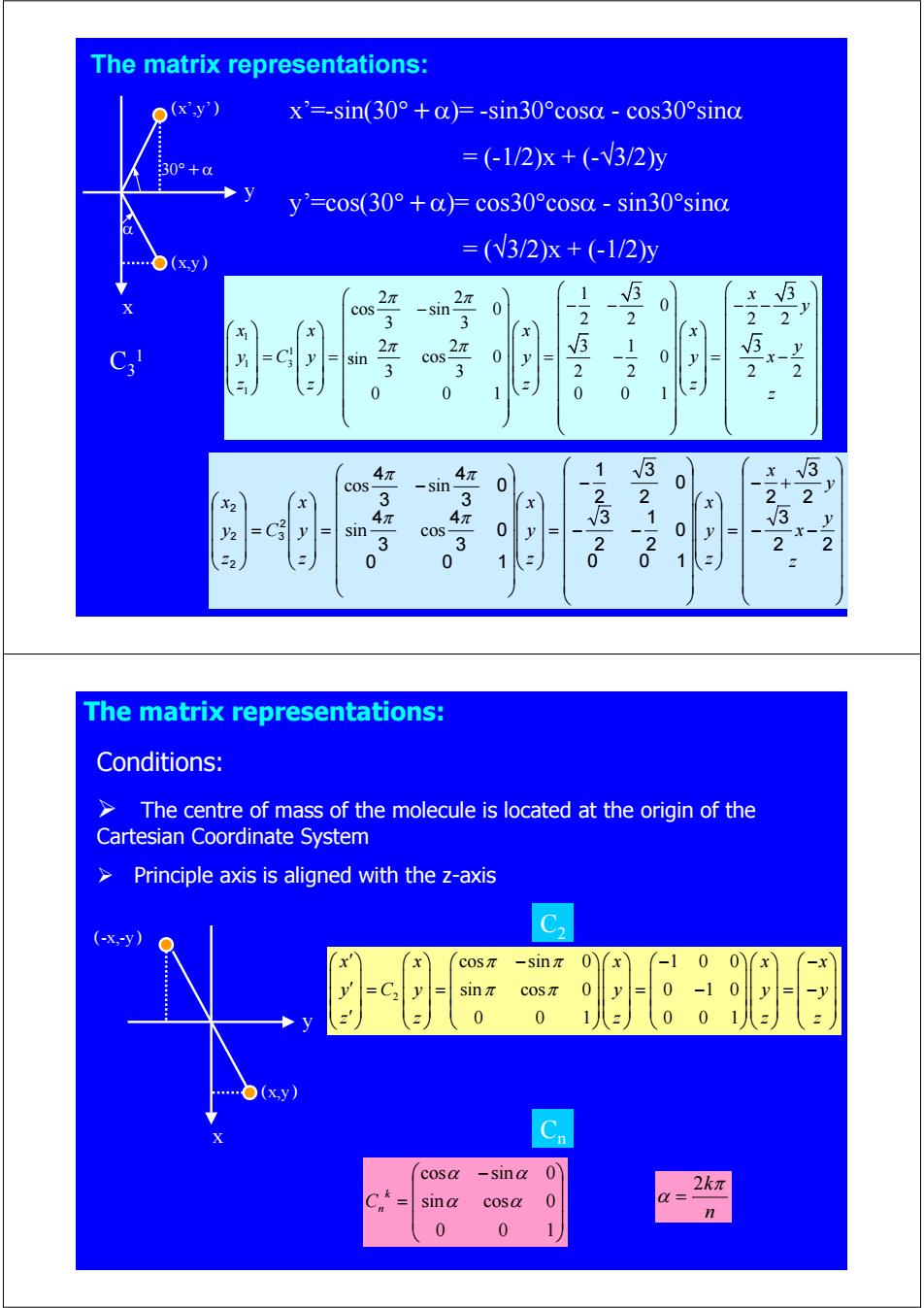
The matrix representations: o(xy) x'=-sin(30°+a)=-sin30°cosa-cos30°sina 30°+a =(-1/2)x+(-V3/2y y'=cos(30°+)=cos30°cosa-sin30°sind =(V3/2)x+(-1/2y (xy) 2π 2π 1 5 cos -sin 0 0 3 3 25 2 2 2 2 x x A N 2π sin 3 cos 3 0 y 0 x-x 2 2 y 0 0 0 0 1 4π 4π 1 3 3 cos sin 0 0 x 4 3 23 2 2 sin cos 0 0 x- 3 3 -20 y 2 2 z 0 0 1 1 The matrix representations: Conditions: > The centre of mass of the molecule is located at the origin of the Cartesian Coordinate System Principle axis is aligned with the z-axis C2 -snπ 0 0) -x sin 0 0 0 1 0 )(xy) cosa -sina 0 2kπ sin a cosa 0 0 0
The matrix representations: 30°+α α (x,y) (x’,y’) C3 1 x y x’=-sin(30°+α)= -sin30°cosα - cos30°sinα = (-1/2)x + (-√3/2)y y’=cos(30°+α)= cos30°cosα - sin30°sinα = (√3/2)x + (-1/2)y ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − − − + = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − − − = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ z y x y x z y x z y x z y x C z y x 2 2 3 2 3 2 0 0 1 0 2 1 2 3 0 2 3 2 1 0 0 1 0 3 4 3 4 0 3 4 3 4 2 3 2 2 2 π π π π sin cos cos sin 1 1 1 3 1 2 2 13 3 cos sin 0 0 3 3 2 2 22 2 2 31 3 cos cos 0 0 3 3 2 2 22 0 01 0 01 x y xx x x y y Cy y y x zz z z z π π π π ⎛ ⎞⎛ ⎞ ⎛ ⎞ − ⎜ ⎟⎜ ⎟ − − −− ⎜ ⎟ ⎛ ⎞ ⎛⎞ ⎛⎞ ⎛⎞ ⎜ ⎟ ⎜⎟ ⎜⎟ ⎜⎟ == = − =− ⎝ ⎠ ⎝⎠ ⎝⎠ ⎝⎠ ⎝ ⎠ ⎝ ⎠⎝ ⎠ sin ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − = 0 0 1 sin cos 0 cos sin 0 α α α α k Cn n kπ α 2 = 2 cos sin 0 1 0 0 sin cos 0 0 1 0 0 0 1 0 01 x x x xx y Cy y y y z z z zz π π π π ⎛ ⎞ ⎛ ⎞ ⎛ ⎞⎛ ⎞ ⎛ ⎞⎛ ⎞ ⎛ ⎞ ′ − − − ⎜ ⎟ ⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎜ ⎟ ′ = = = − =− ′ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠⎝ ⎠ ⎝ ⎠⎝ ⎠ ⎝ ⎠ The matrix representations: C2 Cn (x,y) (-x,-y) x y Conditions: ¾ The centre of mass of the molecule is located at the origin of the Cartesian Coordinate System ¾ Principle axis is aligned with the z-axis

4)Reflection and the Mirror plane (o) >If reflection of an object through a plane produces an indistinguishable configuration then that plane is a plane of symmetry (mirror plane) denoted s. (x.y,-Z 6对 0 0 >There are three types of mirror planes: -If the plane is perpendicular to the vertical principle axis then it labeled on -If the plane contains the principle axis then it is labeled ov. -If a o plane contains the principle axis and bisects the angle between two adjacent 2-fold axes then it is labeled od
¾ If reflection of an object through a plane produces an indistinguishable configuration then that plane is a plane of symmetry (mirror plane) denoted s. 4) Reflection and the Mirror plane (σ) ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − = 0 0 1 0 1 0 1 0 0 σ xy ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ z y x z y x z y x xy 0 0 1 0 1 0 1 0 0 σ (x, y,-z) z (x,y,z) y x ¾There are three types of mirror planes: If the plane is perpendicular to the vertical principle axis then it labeled σh. If the plane contains the principle axis then it is labeled σv. If a σ plane contains the principle axis and bisects the angle between two adjacent 2-fold axes then it is labeled σd

If the plane is perpendicular to the vertical principle axis then it labeled oh Example:BF3 also has a on plane of symmetry C3 9 C2 If the plane contains the principle axis then it is labeled o ● Example:Water Has a C2 principle axis. Has two planes that contain the principle axis,o,and o,. 6
If the plane is perpendicular to the vertical principle axis then it labeled σh. • Example: BF3 also has a σh plane of symmetry. If the plane contains the principle axis then it is labeled σv. • Example: Water – Has a C2 principle axis. – Has two planes that contain the principle axis, σv and σv ’. H H O σv σv