
Example I:Calculation Energy from Frequency Problem:What is the energy of a photon of electromagnetic radiation emitted by an FM radio station at 97.3 x 108 cycles/sec? What is the energy of a gamma ray emitted by Cs137 if it has a frequency of1.60x1020/s? Plan:Use the relationship between energy and frequency to obtain the energy of the electromagnetic radiation (E=hv). Solution: Ehom=hv=(6.626x10-34Js(9.73x10/s)=6.447098x10-24J Ephoton 6.45x10-24 J gamma ray-hv=(6.626x10-34Js(1.60x1020s)=1.06x10-13J gamma ray =1.06x 10-13J Example ll:Calculation of Energy from Wavelength Problem:What is the photon energy ofof electromagnetic radiation that is used in microwave ovens for cooking,if the wavelength of the radiation is 122 mm Plan:Convert the wavelength into meters,then the frequency can be calculated using the relationship;wavelength x frequency =c (where c is the speed of light),then using E=hvto calculate the energy. Solution: wavelength 122 mm 1.22 x 10-m frequency c 3.00x108ms=2.46x100/s wavelength 1.22x10-lm Energy=E=hv=(6.626x10-34Js)(2.46x1010/s)=1.63x10-23J
Example I: Calculation Energy from Frequency Problem: What is the energy of a photon of electromagnetic radiation emitted by an FM radio station at 97.3 x 108 cycles/sec? What is the energy of a gamma ray emitted by Cs137 if it has a frequency of 1.60 x 1020/s? Ephoton =hν = (6.626 x 10 -34Js)(9.73 x 109/s) = 6.447098 x 10 -24J Ephoton = 6.45 x 10 - 24 J Egamma ray =hν = ( 6.626 x 10-34Js )( 1.60 x 1020/s ) = 1.06 x 10 -13J Egamma ray = 1.06 x 10 - 13J Solution: Plan: Use the relationship between energy and frequency to obtain the energy of the electromagnetic radiation (E = hν). Example II: Calculation of Energy from Wavelength Problem: What is the photon energy of of electromagnetic radiation that is used in microwave ovens for cooking, if the wavelength of the radiation is 122 mm ? wavelength = 122 mm = 1.22 x 10 -1m frequency = = = 2.46 x 1010 /s 3.00 x108 m/s 1.22 x 10 -1m c wavelength Energy = E = hν = (6.626 x 10 -34Js)(2.46 x 1010/s) = 1.63 x 10 - 23 J Plan: Convert the wavelength into meters, then the frequency can be calculated using the relationship;wavelength x frequency = c (where c is the speed of light), then using E=hν to calculate the energy. Solution:

Example Ill:Photoelectric Effect The energy to remove an electron from potassium metal is 3.7 x 10-19J.Will photons of frequencies of 4.3 x 1014/s (red light)and 7.5 x 1014 /s (blue light) trigger the photoelectric effect? Ecd=hv=(6.626xl0-34Js)(4.3x1014/s) Ed=2.8x10-19J ·Ee=hv=(6.626xl0-34Js)(7.5x104/s) EMue=5.0x10-19J 。 The binding energy of potassium is 3.7 x 10-19 J 。 The red light will not have enough energy to knock an electron out of the potassium,but the blue light will eject an electron Kinetic Energy of Electron E Electron=ETotal-E Binding Energy E Electron =5.0x10-1J-3.7x10-19J =1.3 x 10-19Joules
Example III: Photoelectric Effect • The energy to remove an electron from potassium metal is 3.7 x 10 -19J. Will photons of frequencies of 4.3 x 1014/s (red light) and 7.5 x 1014 /s (blue light) trigger the photoelectric effect? • E red = hν = (6.626 x10 - 34Js)(4.3 x1014 /s) E red = 2.8 x 10 - 19 J • E blue = hν = (6.626 x10 - 34Js)(7.5x1014 /s) E blue = 5.0 x 10 - 19 J • The binding energy of potassium is = 3.7 x 10 - 19 J • The red light will not have enough energy to knock an electron out of the potassium, but the blue light will eject an electron ! • E Total = E Binding Energy + EKinetic Energy of Electron • E Electron = ETotal - E Binding Energy • E Electron = 5.0 x 10 - 19J - 3.7 x 10 - 19 J = 1.3 x 10 - 19Joules

1.1.3 Atomic and molecular spetra The Line Spectra of Several Elements 341nm 410.1 nm 36,1rm 6553nm 400 450 550 600 650 700 750nm Prism discharg hydrogen Visble spectrum nn 450 50 550 00 650 700 750n 400 450 50 550 e00 60 700 750nm 00 600 700 750 nm
1.1.3 Atomic and molecular spetra The Line Spectra of Several Elements
Planetary model: The electron are like planets---orbit the nucleus Light of energy E given off when electrons change orbits (i.e.,different energies) Why do the electrons not fall into the nucleus? Why only discrete energies? Storage Ring Utility Facilities Users Office (2nd Floor) Main Building A Central 2 自甸国 圃 圆 ☑ User Lounge ☑ ユ一步一談話室 回 Library 固 8 ☒害室 田 日 Liquid Nitrogen Station 液体蜜素補耠 圓 因 圓 Stock Comner 又卜y夕口一才一 面 母 Machine Shop 团 工作室 XGate 田 Health Office 健康管理室 四 Biology Preparation Room ☑ 生物试料準備室 Chemistry Preparation Room 化学赋料準備室 圆 Waste Bin 又卜术y夕又 圍圃 4+ 62 日006的000m
• The electron are like planets --- orbit the nucleus • Light of energy E given off when electrons change orbits (i.e., different energies) Why do the electrons not fall into the nucleus? Why only discrete energies? Planetary model:
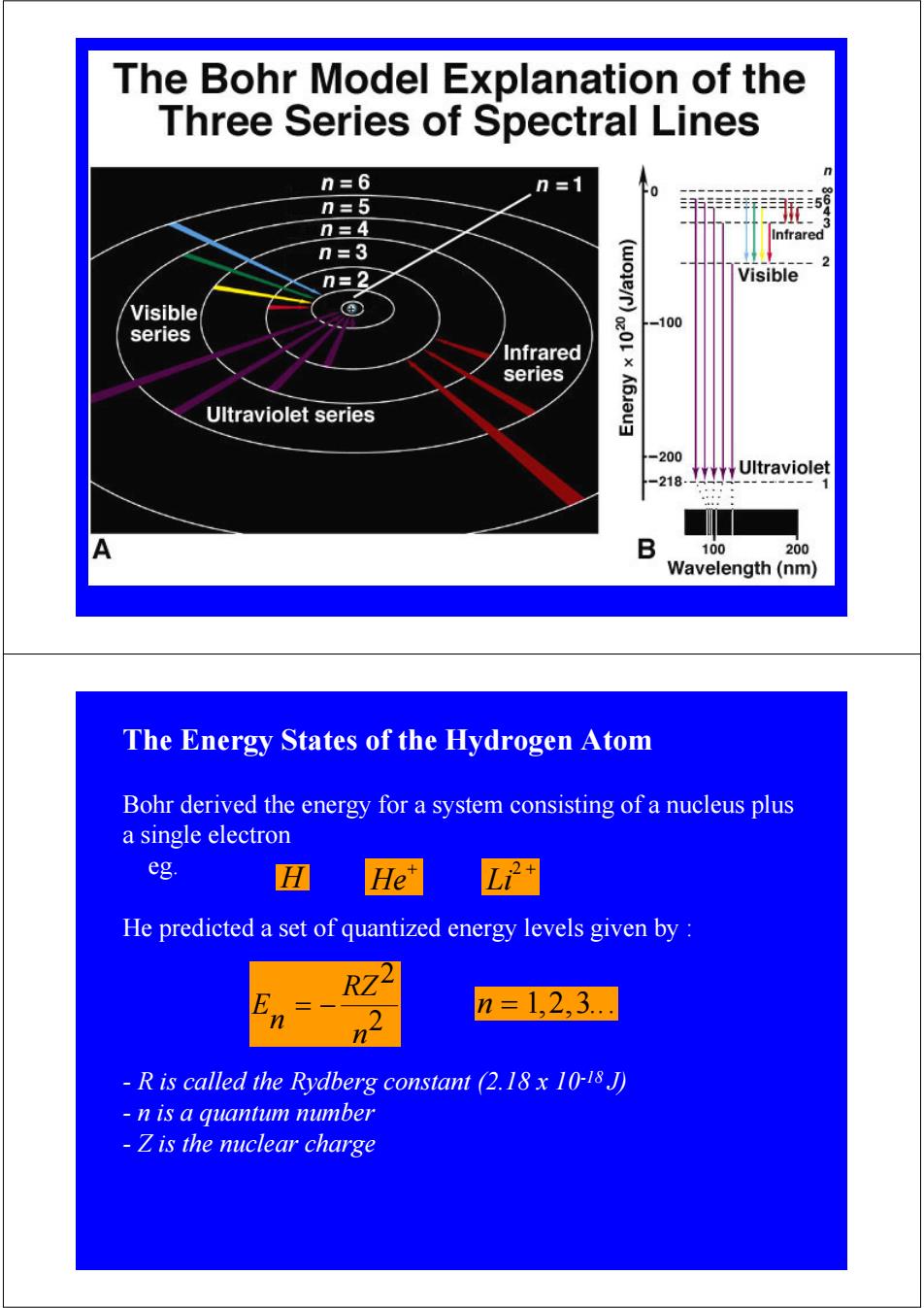
The Bohr Model Explanation of the Three Series of Spectral Lines n=6 n=1 n=5 n=4 Infrared n=3 n=2 Visible Visible ④ -100 series Infrared series × Ultraviolet series 200 Ultraviolet -218 B 100 200 Wavelength(nm) The Energy States of the Hydrogen Atom Bohr derived the energy for a system consisting of a nucleus plus a single electron eg. H He predicted a set of quantized energy levels given by RZ n=1,2,3. -R is called the Rydberg constant (2.18 x 10-18 J) n is a quantum number -Z is the nuclear charge
The Energy States of the Hydrogen Atom Bohr derived the energy for a system consisting of a nucleus plus a single electron eg. He predicted a set of quantized energy levels given by : - R is called the Rydberg constant (2.18 x 10-18 J) - n is a quantum number - Z is the nuclear charge E n = 1,2,3... n = − RZ2 n2 H He+ Li2 +