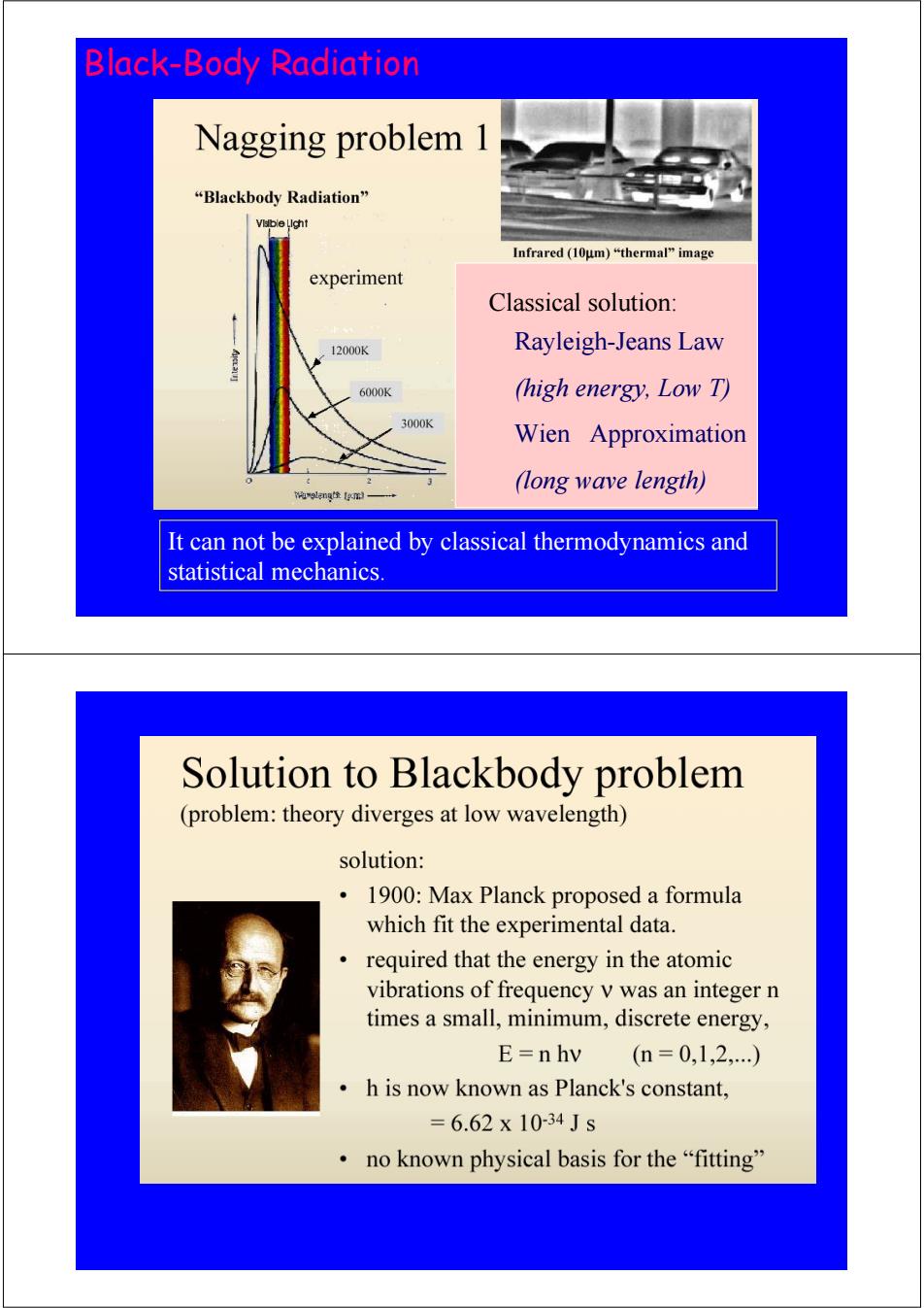
Black-Body Radiation Nagging problem “Blackbody Radiation'” Vlsble Llght Infrared(I0μm)“thermal"image experiment Classical solution: 12000K Rayleigh-Jeans Law 6000K (high energy,Low T) 3000K Wien Approximation (long wave length) 将9知g金m一 It can not be explained by classical thermodynamics and statistical mechanics Solution to Blackbody problem (problem:theory diverges at low wavelength) solution: 1900:Max Planck proposed a formula which fit the experimental data. required that the energy in the atomic vibrations of frequency v was an integer n times a small,minimum,discrete energy, E=n hv (n=0,1,2,…) h is now known as Planck's constant, =6.62x10-34Js no known physical basis for the“fitting
It can not be explained by classical thermodynamics and statistical mechanics. Black-Body Radiation Classical solution: Rayleigh-Jeans Law (high energy, Low T) Wien Approximation (long wave length)

Black Body Radiation Planck showed using quantum mechanics that a black body would emit radiation of the form B,(T)= 2hv3/c2 ehvlkT-1 Many stellar sources can usefully be approximated to be black bodies hv 1 B(T)= 2hv3 e-hvlkT Wien's Approximation (high energy,low T) hv 2v2 <<1 kT B,(T)= kT Rayleigh-Jeans Law (long wavelength,high T) 1.1.2 The photoelectric effect
1.1.2 The photoelectric effect

Nagging problem 2 “Photoelectron effect'” Observed by Hertz in 1887 Light causes electrons to come out of a metal,but only above a threshold frequency v (i.e.,a threshold energy hv) The photoelectric effect Evacuated tube Light sen itive etal plate Positive electrode Current meter Battery
The photoelectric effect
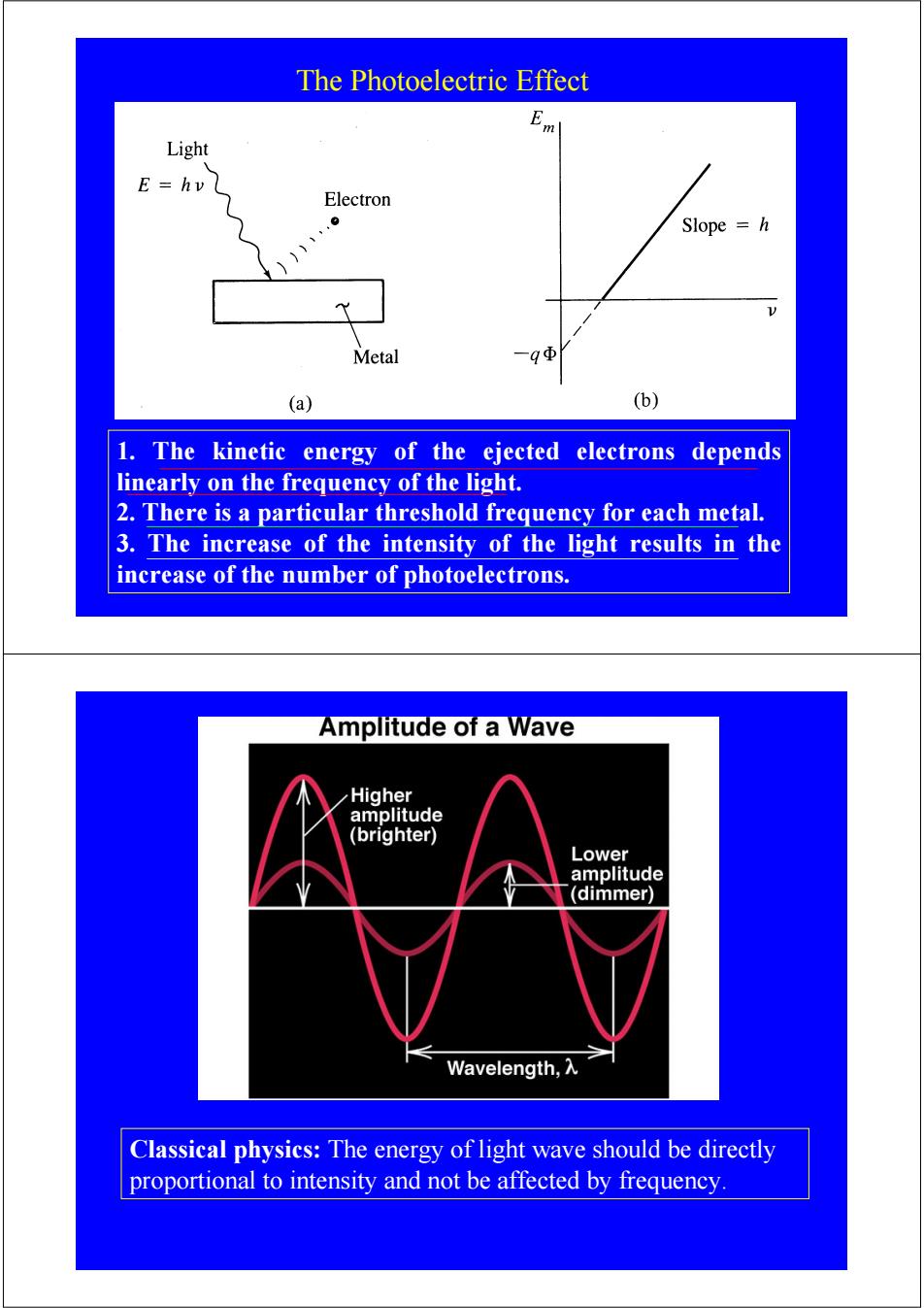
The Photoelectric Effect E Light E=hv Electron Slope h Metal -qΦ (a) (b) 1.The kinetic energy of the ejected electrons depends linearly on the frequency of the light. 2.There is a particular threshold frequency for each metal. 3.The increase of the intensity of the light results in the increase of the number of photoelectrons. Amplitude of a Wave Higher amplitude (brighter) Lower amplitude (dimmer) Wavelength,入 Classical physics:The energy of light wave should be directly proportional to intensity and not be affected by frequency
The Photoelectric Effect 1. The kinetic energy of the ejected electrons depends linearly on the frequency of the light. 2. There is a particular threshold frequency for each metal. 3. The increase of the intensity of the light results in the increase of the number of photoelectrons. Classical physics: The energy of light wave should be directly proportional to intensity and not be affected by frequency

Explaining the Photoelectric Effect Albert Einstein Proposed a corpuscular theory of light (photons) won the Nobel prize in 1921 1.Light consists of a stream of photons.The energy of a photon is proportional to its frequency. e三hv h=Planck's constant 2.A photon has energy as well as mass.m=hv /e2 3.A photon has a definite momentum.p=mc=hv /c=h/ 4.The intensity of light depends on the photon density Explaining the Photoelectric Effect Therefore,the photon's energy is equaled to the electron's kinetic energy added to the electron's binding energy Ephoton=E binding +E Kinetic energy hv=W+E
Explaining the Photoelectric Effect • Albert Einstein – Proposed a corpuscular theory of light (photons). – won the Nobel prize in 1921 1. Light consists of a stream of photons. The energy of a photon is proportional to its frequency. ε = hν h = Planck’s constant 2. A photon has energy as well as mass. m= hν /c2 3. A photon has a definite momentum. p=mc= hν /c=h/λ 4. The intensity of light depends on the photon density Therefore, the photon’s energy is equaled to the electron’s kinetic energy added to the electron’s binding energy • Ephoton = E binding + E Kinetic energy • hν=W+Ek Explaining the Photoelectric Effect