《大学物理》课程教学资源（PPT课件讲稿）第八章 静电场和稳恒电场

8.1.6带电体在外电场中所受的作用 (1)带电体在匀强场中： F=gE （2)带电体在非匀强场中： F-∫Edg 21 首页上页下页退出

首 页 上 页 下 页 退 出 21 8.1.6 带电体在外电场中所受的作用 （１） 带电体在匀强场中： F qE   = （２） 带电体在非匀强场中：  = Q F Edq  

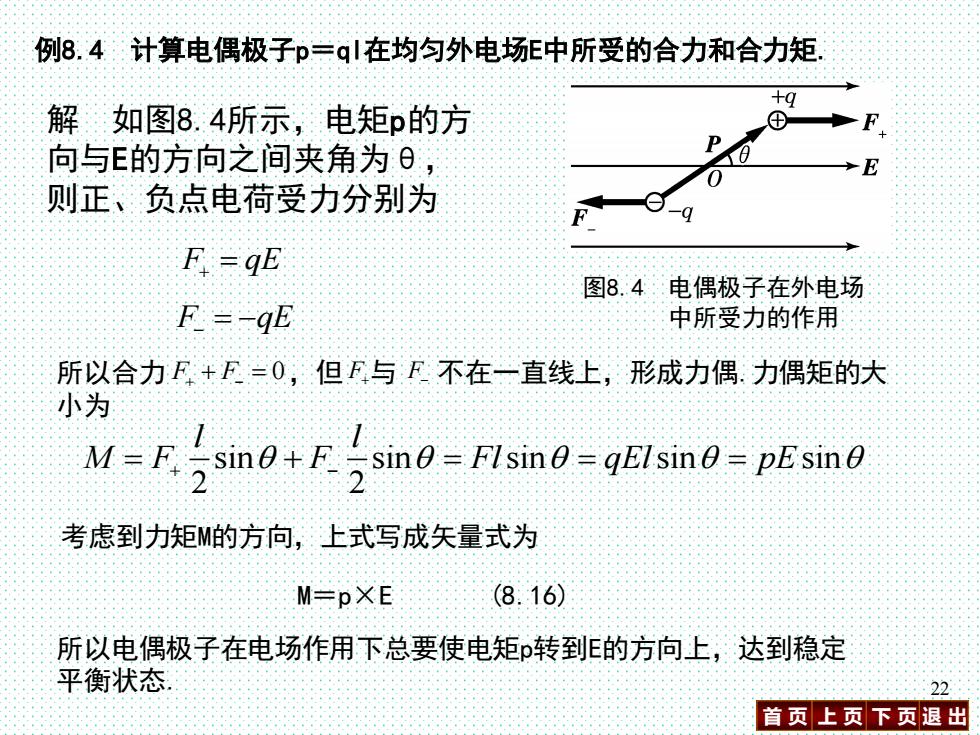
例8.4计算电偶极子p=ql在均匀外电场E中所受的合力和合力矩， +9 解如图8.4所示，电矩p的方 向与E的方向之间夹角为， 则正、负点电荷受力分别为 F=gE 图84电偶极子在外电场 F=-9E 中所受力的作用 所以合力F+F=0,但F与F不在一直线上，形成力偶：力偶矩的大 小 M=F.sin0Fsin0=FIsin0-qFIsin0-pEsin0 2 考虑到力矩M的方向，上式写成矢量式为 M-pXE (8.16) 所以电偶极子在电场作用下总要使电矩转到的方向上，达到稳定 平衡状态 22 首页上页下页退出

首 页 上 页 下 页 退 出 22 例8.4 计算电偶极子p＝ql在均匀外电场E中所受的合力和合力矩. 解 如图8.4所示，电矩p的方 向与E的方向之间夹角为θ， 则正、负点电荷受力分别为 sin sin sin sin sin 2 2 l l M F F Fl qEl pE = + = = = + −      图8.4 电偶极子在外电场 中所受力的作用 F qE + = F qE − = − 所以合力 ，但 与 不在一直线上，形成力偶.力偶矩的大 小为 F F 0 + − + = F+ F− 考虑到力矩M的方向，上式写成矢量式为 M＝p×E (8.16) 所以电偶极子在电场作用下总要使电矩p转到E的方向上，达到稳定 平衡状态

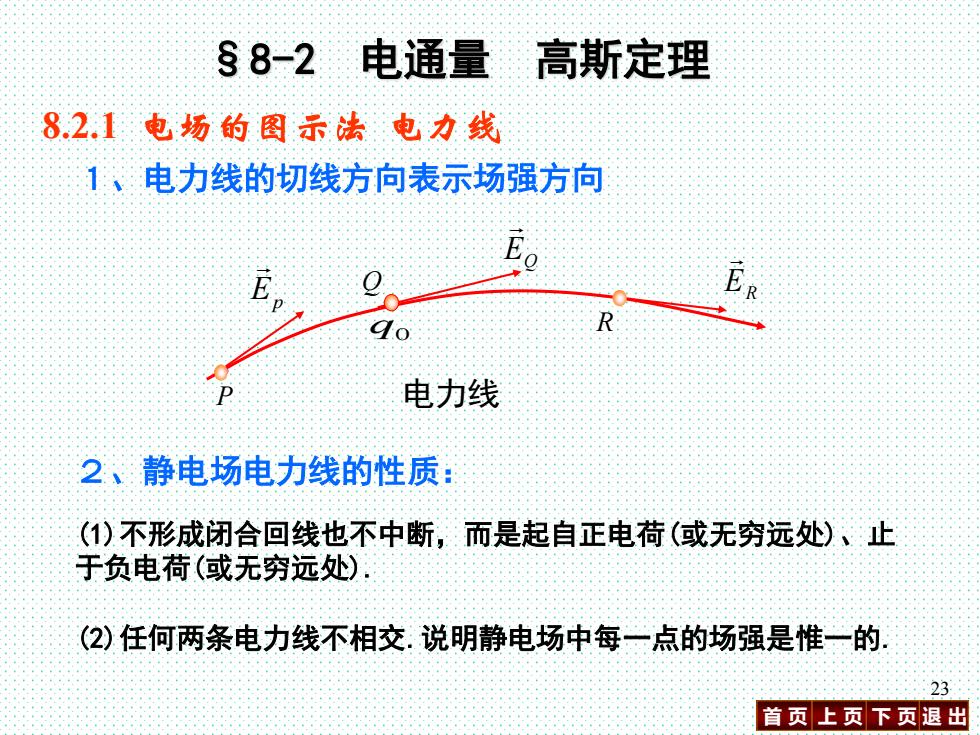
§8-2 电通量 高斯定理 8.2.1电场的图示法电力线 1、电力线的切线方向表示场强方向 E。 E E o 电力线 2、静电场电力线的性质： (1)不形成闭合回线也不中断，而是起自正电荷（或无穷远处）、止 于负电荷（或无穷远处）. (2)任何两条电力线不相交.说明静电场中每一点的场强是惟一的 23 首页上页下页退出

首 页 上 页 下 页 退 出 23 8.2.1 电场的图示法 电力线 １、电力线的切线方向表示场强方向 ２、静电场电力线的性质： (1)不形成闭合回线也不中断，而是起自正电荷(或无穷远处)、止 于负电荷(或无穷远处). 电力线 Q q0 EQ  R ER  P Ep  (2)任何两条电力线不相交.说明静电场中每一点的场强是惟一的. §8-2 电通量 高斯定理

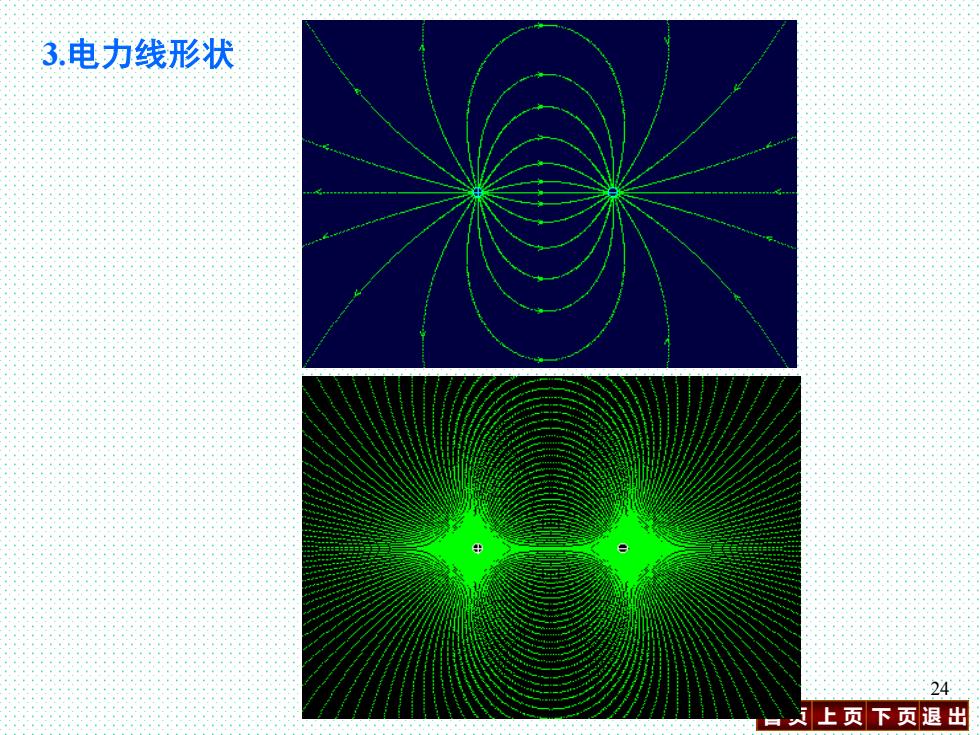
3.电力线形状 24 过上页下页退出

首 页 上 页 下 页 退 出 24 3.电力线形状

8.2.2电通量 1、定义：通过电场中任一给定截面的电力线的总数称为通 过该截面的电通量，记为。 2、电通量的计算 在匀强场中（平面）(E与S平行S=Sn) 0 4。=EAS,=EAS=EAS cos0° φ。=E4S 在匀强场中(E与成0角) φ。=EASL=E4Scos0 4。=E·1S 25 首页上页下页退出

首 页 上 页 下 页 退 出 25 8.2.2 电通量 ２、电通量的计算 e E S    =  e = ES⊥ = ES cos e E S    =  １、定义：通过电场中任一给定截面的电力线的总数称为通 过该截面的电通量，记为e 在匀强场中(平面）(E与S平行 S=Sn0） 在匀强场中(E与S成 角 ） e = ES⊥ = ES  = ES cos0 / S E  n0 S E  S n0 