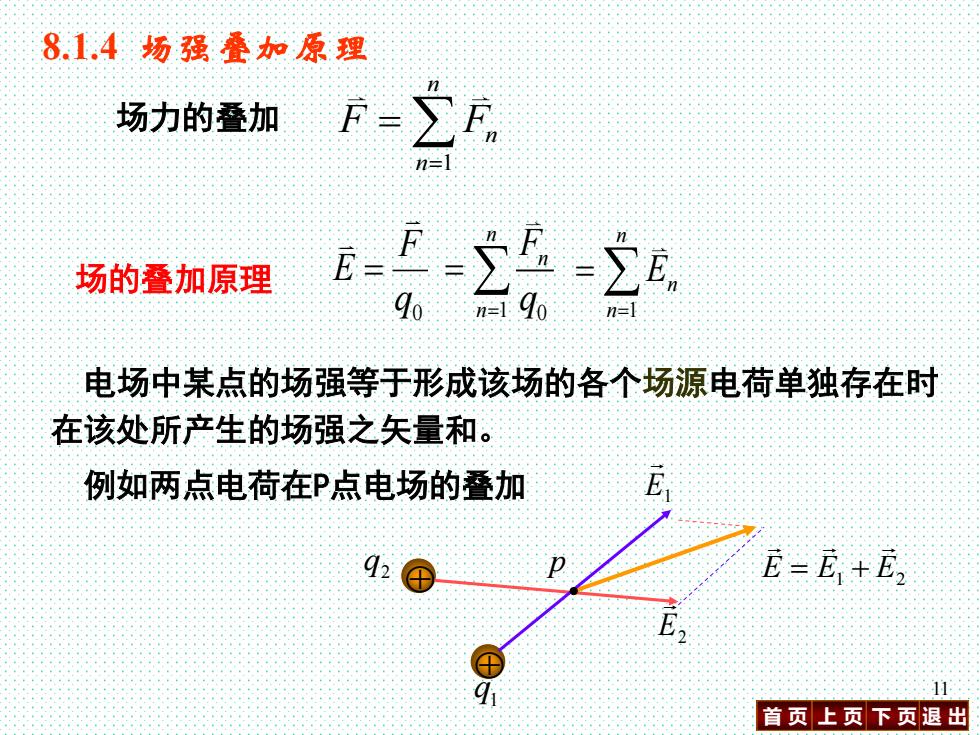
8.1.4场强叠如加原理 场力的叠加 f- 公 n=1 场的叠加原理 E-F-) -E. 90 电场中某点的场强等于形成该场的各个场源电荷单独存在时 在该处所产生的场强之矢量和。 例如两点电荷在P点电场的叠加 E 92 E=E+E 首页上页下页退出
首 页 上 页 下 页 退 出 11 8.1.4 场强叠加原理 场力的叠加 1 n n n F F = = 场的叠加原理 电场中某点的场强等于形成该场的各个场源电荷单独存在时 在该处所产生的场强之矢量和。 例如两点电荷在P点电场的叠加 0 q F E = 1 0 n n n F = q = 1 n n n E = = E E1 E2 = + E2 q2 1 q E1 p
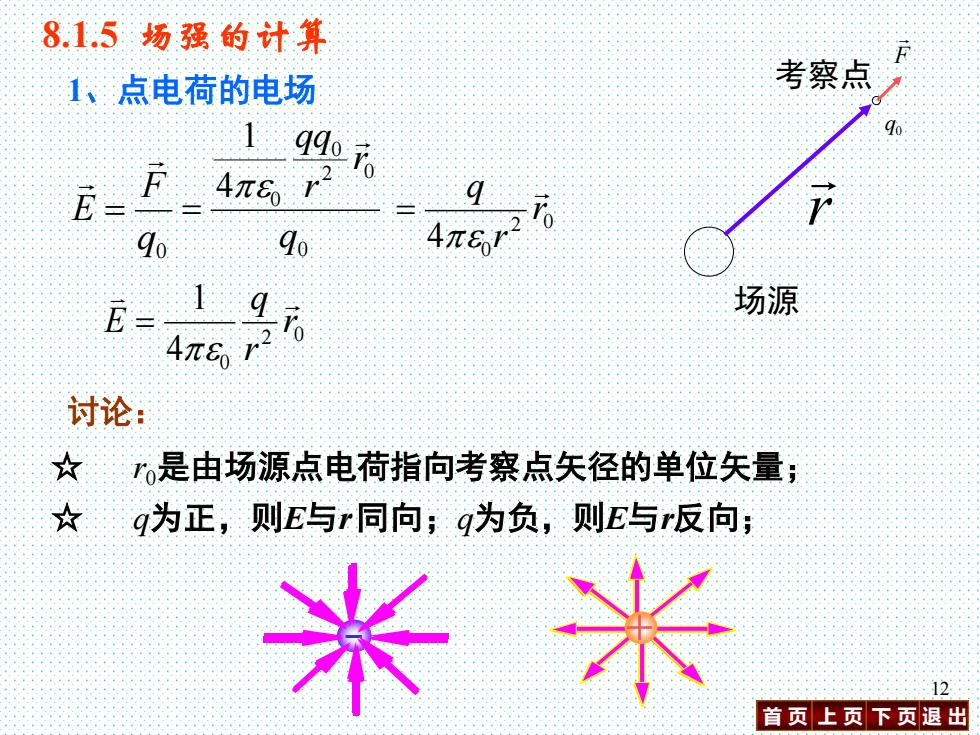
8.1.5场强的计算 1、点电荷的电场 考察点 qdo ro E- F 4π6r 26 90 90 E= 1 场源 4π6r 讨论: 女 r是由场源点电荷指向考察点矢径的单位矢量; ☆ q为正,则E与r同向;q为负,则E与r反向; 米米 12 首页上页下页退出
首 页 上 页 下 页 退 出 12 8.1.5 场强的计算 1、点电荷的电场 2 0 0 4 1 r r q E = 讨论: ☆ r0是由场源点电荷指向考察点矢径的单位矢量; ☆ q为正,则E与r 同向;q为负,则E与r反向; q0 F E = 0 2 0 0 4 0 1 q r r qq = 2 0 4 0 r r q = r 场源 考察点 0 q F +

☆ →∞,则E=0 →0,则E→∞,点电荷模型不成立。 ☆在各向同性均匀无限大的电介质中 F= 990 9 4π88,r - 各向同性均匀无限大电介质中的场强等于真空中场强的/6 这个结论可以推广到:各向同性均匀电介质均匀充满两等 势面之间的场强,等于真空中场强的1/ε。 2、点电荷系的电场 E= 13 首页上页下页退出
首 页 上 页 下 页 退 出 13 ☆ r→∞,则 E = 0 r→0 ,则 E →∞ ,点电荷模型不成立。 ☆ 在各向同性均匀无限大的电介质中 2 0 0 0 4 r r qq F r = r r E r r q E 0 2 0 4 0 = = 2、 点电荷系的电场 2 0 1 4 0 i i i n i r r q E = = 各向同性均匀无限大电介质中的场强等于真空中场强的 r 1 这个结论可以推广到:各向同性均匀电介质均匀充满两等 势面之间的场强,等于真空中场强的 1/ r

3、电荷连续分布的带电体的电场 将其分割成点电荷系,求每个点电荷元的电场 dE dg P O 然后对所有点电荷元求积分: B-S dq dq 带电体 dg=pdv 带电面 dq=o dS 带电线 dq=λdl 首页上页下页退出
首 页 上 页 下 页 退 出 14 3、 电荷连续分布的带电体的电场 将其分割成点电荷系,求每个点电荷元的电场 2 0 4 0 r r dq dE = 然后对所有点电荷元求积分: 2 0 0 V 4 dq E r r = 带电体 dq= dV 带电面 dq= dS 带电线 dq= dl E d V P dq

例8.2真空中有一均匀带电直线,长为L,总电量9,试求 距直线上距离为a的P点的场强: 解见图8.2,取P点到L的垂足0点为坐标原点,x轴与y轴 正向如图所示.P点到1两端的连线与x轴正方向的夹角分别 为0和A:线元dx位于x处,则g=d=号k,dq在P点产生 的场强dE方向如图,大小为 I Adx dE= 4πr2 r为P点到dx的距离,r与x正向的 夹角为日,则 dE,=dE cos0 图8.2均匀带电直线外任一点的场强 dE,=dE sin 15 首页上页下页退出
首 页 上 页 下 页 退 出 15 例8.2 真空中有一均匀带电直线,长为L,总电量q,试求 距直线上距离为a的P点的场强. 解 见图8.2,取P点到L的垂足O点为坐标原点,x轴与y轴 正向如图所示.P点到l两端的连线与x轴正方向的夹角分别 为 和 .线元dx位于x处,则 ,dq在P点产生 的场强dE方向如图,大小为 1 2 q dq dx dx L = = 2 0 1 4 dx dE r = 图8.2 均匀带电直线外任一点的场强 r为P点到dx的距离,r与x正向的 夹角为θ,则 cos x dE dE = sin y dE dE =