
运动粘度:流体粘度μ与密度ρ之比称为运动粘度, 用符号ν表示 ν=μ/ρ (1-34) 其单位为m 2/s。而CGS单位制中,其单位为cm 2/s,称为斯托 克斯,用符号St表示。 各种液体和气体的粘度数据,均由实验测定。可在有关手 册中查取某些常用液体和气体粘度的图表。 温度对液体粘度的影响很大,当温度升高时,液体的粘度 减小,而气体的粘度增大。压力对液体粘度的影响很小,可忽 略不计,而气体的粘度,除非在极高或极低的压力下,可以认 为与压力无关
运动粘度:流体粘度μ与密度ρ之比称为运动粘度, 用符号ν表示 ν=μ/ρ (1-34) 其单位为m 2/s。而CGS单位制中,其单位为cm 2/s,称为斯托 克斯,用符号St表示。 各种液体和气体的粘度数据,均由实验测定。可在有关手 册中查取某些常用液体和气体粘度的图表。 温度对液体粘度的影响很大,当温度升高时,液体的粘度 减小,而气体的粘度增大。压力对液体粘度的影响很小,可忽 略不计,而气体的粘度,除非在极高或极低的压力下,可以认 为与压力无关
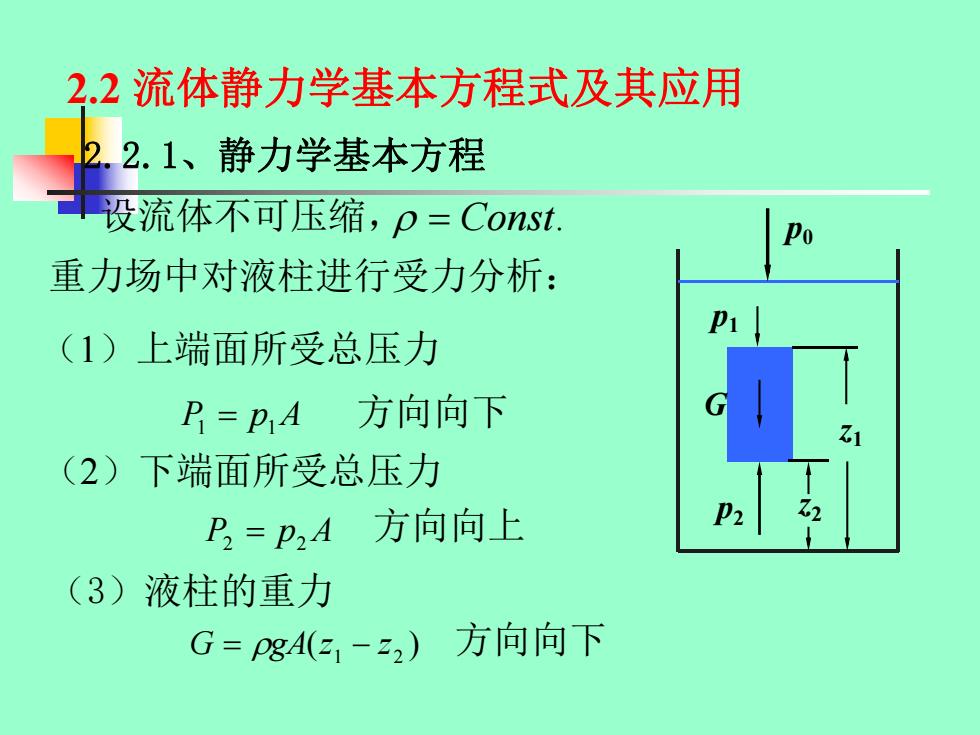
2.2 流体静力学基本方程式及其应用 2.2.1、静力学基本方程 重力场中对液柱进行受力分析: P1 p1A (1)上端面所受总压力 P2 p2A (2)下端面所受总压力 (3)液柱的重力 ( ) 1 2 G gA z z 设流体不可压缩, Const. p0 p2 p1 z1 z2 方向向下 G 方向向上 方向向下
2.2 流体静力学基本方程式及其应用 2.2.1、静力学基本方程 重力场中对液柱进行受力分析: P1 p1A (1)上端面所受总压力 P2 p2A (2)下端面所受总压力 (3)液柱的重力 ( ) 1 2 G gA z z 设流体不可压缩, Const. p0 p2 p1 z1 z2 方向向下 G 方向向上 方向向下

液柱处于静止时,上述三项力的合力为零: p2A p1A gA(z1 z2 ) 0 ——静力学基本方程 压力形式 能量形式 ( ) 2 1 1 2 p p g z z z g p z g p 2 2 1 1
液柱处于静止时,上述三项力的合力为零: p2A p1A gA(z1 z2 ) 0 ——静力学基本方程 压力形式 能量形式 ( ) 2 1 1 2 p p g z z z g p z g p 2 2 1 1

讨论: (1)适用于重力场中静止、连续的同种不可压缩性 流体; (2)物理意义: zg ——单位质量流体所具有的位能,J/kg; p ——单位质量流体所具有的静压能,J/kg。 在同一静止流体中,处在不同位置流体的位 能和静压能各不相同,但二者可以转换,其总和 保持不变
讨论: (1)适用于重力场中静止、连续的同种不可压缩性 流体; (2)物理意义: zg ——单位质量流体所具有的位能,J/kg; p ——单位质量流体所具有的静压能,J/kg。 在同一静止流体中,处在不同位置流体的位 能和静压能各不相同,但二者可以转换,其总和 保持不变

(3)在静止的、连续的同种流体内,处于同一水 平面上各点的压力处处相等。压力相等的面称为 等压面。 (4)压力具有传递性:液面上方压力变化时,液 体内部各点的压力也将发生相应的变化
(3)在静止的、连续的同种流体内,处于同一水 平面上各点的压力处处相等。压力相等的面称为 等压面。 (4)压力具有传递性:液面上方压力变化时,液 体内部各点的压力也将发生相应的变化