
第三届全国周培源大学生力学竞赛理论力学试题 下面共计25分,请根据问题的类型将正确结果填写在答案纸上,全卷满分为120分。 一、是非题(共5题,每题3分,请在答案纸的相应题号括弧内填“是”或“非”) (1)一空间力系,若力作用线与某一固定直线相平行,则其独立的平衡方程只有5个。 (2)牵连运动为定轴转动时,不一定有科氏加速度。 (3)平面刚体各点的动量对一轴的动量矩之和可以用作用于质心的刚体动量对该轴的动量矩表示。 (4)平面运动刚体上惯性力系的合力必作用在刚体的质心上。 (5)拉氏二类方程的适用范围是完整、理想约束,而动力学普遍方程则没有这些限制。 二、选择题(共5题,每题3分,请将答案的序号填入答案纸的相应题号括弧内) (6)已知一正方体,各边长a,沿对角线BH作用一个力F, 2◆ H 则该力在x,轴上的投影为() G ②F/W2: E ①0: ③F/V6: ④-F/5。 A (7)三角形楔块B置于楔块A的斜面上,若A块以v4=3ms的速度向左运动,=30°,则B 块的速度vg=()ms。 LLLL2 B ①3:②2/3:③3:④√3/3. (8)在图示系统中,滑块A以匀速度v4=1m/s向 下运动,杆CD长1m,当a=45°且杆水平时,AB i0.5m 杆的角速度OB=( )rad/s,CD杆的角速度 0cp=( )rad/s。 0.5m ①0:②0.5:③1.0:④√2。 (9)以弹簧常数为k的弹簧下挂一质量为m的物体,若物体从静平衡位置(设静伸长为δ)下降 △距离,则弹性力所做的功为()。 @:②6+4:®6+4-:@62-6+4)
第三届全国周培源大学生力学竞赛理论力学试题 下面共计 25 分,请根据问题的类型将正确结果填写在答案纸上,全卷满分为 120 分。 一、是非题(共 5 题,每题 3 分,请在答案纸的相应题号括弧内填“是”或“非”) (1)一空间力系,若力作用线与某一固定直线相平行,则其独立的平衡方程只有 5 个。 (2)牵连运动为定轴转动时,不一定有科氏加速度。 (3)平面刚体各点的动量对一轴的动量矩之和可以用作用于质心的刚体动量对该轴的动量矩表示。 (4)平面运动刚体上惯性力系的合力必作用在刚体的质心上。 (5)拉氏二类方程的适用范围是完整、理想约束,而动力学普遍方程则没有这些限制。 二、选择题(共 5 题,每题 3 分,请将答案的序号填入答案纸的相应题号括弧内) (6)已知一正方体,各边长a ,沿对角线 BH 作用一个力 F , A O B C D H G F E x y z 1 x 则该力在 轴上的投影为() 1 x ① 0; ② F 2 ; ③ F 6 ; ④ − F 3 。 (7)三角形楔块 B 置于楔块 A 的斜面上,若 A 块以 = 3m s A v 的速度向左运动, ,则 B 块的速度 o α = 30 = ( ) m s B v 。 A v A α B ① 3 ;②2 3 ;③3;④ 3 3。 (8)在图示系统中,滑块 A 以匀速度 = 1m s A v 向 下运动,杆 CD 长1m ,当 且杆水平时,AB 杆的角速度 o α = 45 = ( )rad s ω AB ,CD 杆的角速度 = ( )rad s ωCD 。 ① 0;② 0.5;③ 1.0;④ 2 。 (9)以弹簧常数为k 的弹簧下挂一质量为m 的物体,若物体从静平衡位置(设静伸长为δ )下降 ∆ 距离,则弹性力所做的功为( )。 A C D B A v α 0.5m 0.5m ① 2 2 1 k∆ ;② 2 ( ) 2 1 k δ + ∆ ;③ (( ) ) 2 1 2 2 k δ + ∆ −δ ;④ ( ( ) ) 2 1 2 2 k δ − δ + ∆ 1
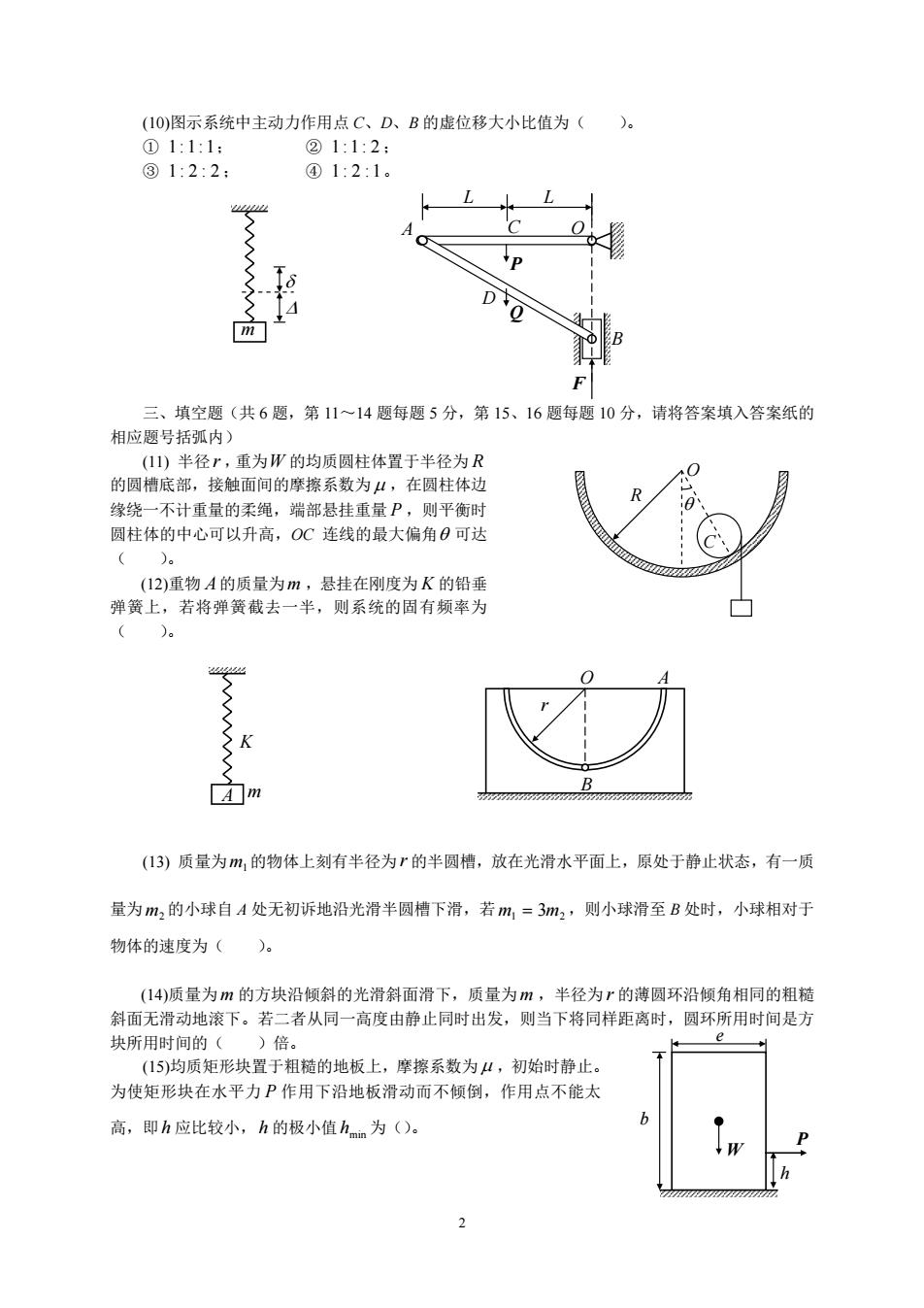
(1O)图示系统中主动力作用点C、D、B的虚位移大小比值为()。 ①1:1:1: ②1:1:2: ③1:2:2: ④1:2:1。 2☑ D m 三、填空题(共6题,第11~14题每题5分,第15、16题每题10分,请将答案填入答案纸的 相应题号括弧内) (11)半径P,重为W的均质圆柱体置于半径为R 的圆槽底部,接触面间的摩擦系数为4,在圆柱体边 R 缘绕一不计重量的柔绳,端部悬挂重量P,则平衡时 圆柱体的中心可以升高,OC连线的最大偏角日可达 ()。 (12)重物A的质量为m,悬挂在刚度为K的铅垂 弹簧上,若将弹簧截去一半,则系统的固有频率为 ()。 K A m 000W0W0 (13)质量为m1的物体上刻有半径为”的半圆槽,放在光滑水平面上,原处于静止状态,有一质 量为m2的小球自A处无初诉地沿光滑半圆槽下滑,若m1=3m2,则小球滑至B处时,小球相对于 物体的速度为()。 (14)质量为m的方块沿倾斜的光滑斜面滑下,质量为m,,半径为r的薄圆环沿倾角相同的粗糙 斜面无滑动地滚下。若二者从同一高度由静止同时出发,则当下将同样距离时,圆环所用时间是方 块所用时间的()倍。 e (15)均质矩形块置于粗糙的地板上,摩擦系数为4,初始时静止。 为使矩形块在水平力P作用下沿地板滑动而不倾倒,作用点不能太 高,即h应比较小,h的极小值hmim为()。 6 w☑
(10)图示系统中主动力作用点 C、D、B 的虚位移大小比值为( )。 ① 1: 1: 1; ② 1 : 1 : 2 ; ③ 1: 2 : 2 ; ④ 1 : 2 : 1。 A C O P Q D B F L L δ ∆ m 三、填空题(共 6 题,第 11~14 题每题 5 分,第 15、16 题每题 10 分,请将答案填入答案纸的 相应题号括弧内) (11) 半径 r ,重为W 的均质圆柱体置于半径为 R 的圆槽底部,接触面间的摩擦系数为 µ ,在圆柱体边 缘绕一不计重量的柔绳,端部悬挂重量 P ,则平衡时 圆柱体的中心可以升高,OC 连线的最大偏角θ 可达 ( )。 O R C θ (12)重物 A 的质量为m ,悬挂在刚度为 K 的铅垂 弹簧上,若将弹簧截去一半,则系统的固有频率为 ( )。 K A m O A r B (13) 质量为m1的物体上刻有半径为 r 的半圆槽,放在光滑水平面上,原处于静止状态,有一质 量为m2 的小球自 A 处无初诉地沿光滑半圆槽下滑,若m1 = 3m2 ,则小球滑至 B 处时,小球相对于 物体的速度为( )。 (14)质量为 m 的方块沿倾斜的光滑斜面滑下,质量为 m ,半径为 r 的薄圆环沿倾角相同的粗糙 斜面无滑动地滚下。若二者从同一高度由静止同时出发,则当下将同样距离时,圆环所用时间是方 块所用时间的( )倍。 e h P W b (15)均质矩形块置于粗糙的地板上,摩擦系数为 µ ,初始时静止。 为使矩形块在水平力 P 作用下沿地板滑动而不倾倒,作用点不能太 高,即h 应比较小,h 的极小值hmin 为()。 2

(16)从载人飞船上观察到地球海洋某处有一作逆时针旋转的稳定的海洋环流,旋转周期是16小 时。可以确定,这个海洋环流处于()半球,纬度为()度。 四、综合分析题(A)(每题5分,答案请写在答案纸相应题号的括弧内) 均质圆盘的半径为”,可绕其中心O在铅垂平面内自由转动, 转动惯量为I,一质量为m的甲虫M,以不变的相对速度u沿此 圆盘的边缘运动,初瞬时,圆盘静止不动,甲虫M位于圆盘的最 底部,且己有相对速度u。 (17)圆盘的运动微分方程是(以转角0表示)是()。 (18)甲虫M的绝对运动微分方程是(以OM连线的转角B 表示)是()。 (19)圆盘沿切线方向给甲虫的作用力是()。 M y (20)甲虫能升高到与O点相同高度的条件是()。 五、综合分析题(B)(每题6分,答案请写在答案纸相应题号的括弧内) 质量为M的薄方圆盘上有一半径为R的光滑圆槽,方盘的质心在圆心O点。方盘对O的回转 半径为p。在圆槽内有一质量为m的小球B。将该系统静止地放置在光滑的水平面上。现给小球B 一沿圆周切线方向的冲击,使小球突然有一沿圆周切线方向的初速度V。,试求此后系统的运动。 (21)系统的自由度数是()。 (22)系统质心作()运动,其速度大小为()。 (23)在随系统质心运动的平动坐标系中观察,方盘作()运动,其质心0的轨迹是(), 速度大小为()。 (24)在上述平动坐标系中观察,小球B作()运动,速度大小为()。 (25)方盘对小球的作用力大小为(),方向()。 o 2
(16)从载人飞船上观察到地球海洋某处有一作逆时针旋转的稳定的海洋环流,旋转周期是 16 小 时。可以确定,这个海洋环流处于( )半球,纬度为( )度。 四、综合分析题(A)(每题 5 分,答案请写在答案纸相应题号的括弧内) 均质圆盘的半径为 r ,可绕其中心 O 在铅垂平面内自由转动, 转动惯量为 I ,一质量为m 的甲虫 M ,以不变的相对速度 沿此 圆盘的边缘运动,初瞬时,圆盘静止不动,甲虫 u M 位于圆盘的最 底部,且已有相对速度u 。 M O θ ϕ y (17) 圆盘的运动微分方程是(以转角ϕ 表示)是( )。 (18) 甲虫 M 的绝对运动微分方程是(以OM 连线的转角θ 表示)是( )。 (19) 圆盘沿切线方向给甲虫的作用力是( )。 (20) 甲虫能升高到与 O 点相同高度的条件是( )。 五、综合分析题(B)(每题 6 分,答案请写在答案纸相应题号的括弧内) 质量为 M 的薄方圆盘上有一半径为 R 的光滑圆槽,方盘的质心在圆心 O 点。方盘对 O 的回转 半径为 ρ 。在圆槽内有一质量为 的小球 B。将该系统静止地放置在光滑的水平面上。现给小球 B 一沿圆周切线方向的冲击,使小球突然有一沿圆周切线方向的初速度 ,试求此后系统的运动。 m 0 v (21) 系统的自由度数是()。 (22) 系统质心作( )运动,其速度大小为( )。 (23) 在随系统质心运动的平动坐标系中观察,方盘作( )运动,其质心 O 的轨迹是( ), 速度大小为( )。 (24) 在上述平动坐标系中观察,小球 B 作( )运动,速度大小为( )。 (25) 方盘对小球的作用力大小为( ),方向( )。 O B 0 v 3

第三届全国过周培源大学生力学竞赛理论力学试题解答 一、是非题 (1)非(2)是 (3)是(4)非 (⑤)非 二、选择题 (6)①(7)① (8)③①(9)④(10)③ 三、填空题 (11)arctan u (12)√2k/m (13)动能定理 1 mm+2m:--0=m%gr 1 动量定理 mv。+m2(v。-y,)=0 (m1+m2P。=m2', 己知 m1=3m2得y,=4v。 代入动能定理 3v2+9v2=2g 得 2W6后 .=V68r,v= (14)动能定理 1 方块下滑,乏m=mgs sin8 得,a1=mgy1sin0,a1=gsin0 4 圆环下滚, m) =ngs sin0或 2 mgssin 得2w2a2=mgY2sin0,a2= 1 1 21 a 故 g-4=2,万=m (15)当h过小时,矩形块可能绕A点向后倾倒。考虑临界情况: b 动静法P=Q+F P Ph+W=0号 b 2 A N=W F=uN 得P政+r含=e-m月 2 b W 2-2p(ub+c) 废s产r-n⅓-i网 4
第三届全国过周培源大学生力学竞赛理论力学试题解答 一、是非题 (1) 非 (2) 是 (3) 是 (4) 非 (5) 非 二、选择题 (6) ① (7) ① (8) ③① (9) ④ (10)③ 三、填空题 (11) arctan µ (12) 2 k m (13) 动能定理 m m m ( ) v v m gr e e r 2 2 2 2 1 0 2 1 2 1 + − − = O A r B e v r v 动量定理 m1ve + m2 ( ) ve − vr = 0 ( ) e r m m v m v 1 + 2 = 2 已知 m1 = 3m2 得 r e v = 4v 代入动能定理 v v gr e e 3 9 2 2 2 + = 得 v gr e 6 1 = ,v gr r 3 2 6 = (14) 动能定理 方块下滑, sinθ 2 1 2 mv1 = mgs 得 mv1a1 = mgv1 sinθ , a1 = g sinθ 圆环下滚, ( ) sinθ 2 1 2 1 2 2 2 2 2 mgs r v mv mr ⎟ = ⎠ ⎞ ⎜ ⎝ ⎛ + 或 2 sinθ 2 1 2 mv2 = mgs 得 θ sinθ 2 1 2 sin , mv2a2 = mgv2 a2 = g 但 2 2 2 2 1 1 2 1 , 2 1 s = a T s = a T 故 2 1 2 1 2 1 2 2 2,T 2T a a T T = = = (15) 当h 过小时,矩形块可能绕 A 点向后倾倒。考虑临界情况: a hmin P W b A c Q F N 动静法 P = Q + F 2 2 min b Q c Ph +W = N = W F = µN 得 ( ) 2 2 min b P W c Ph +W = − µ ( ) b c P b W h = − µ + 2 2 min 或 [ ] (P W )b Wc P h = − µ − 2 1 min 4

当P(a+r时,上:当<P(+}时,=0, b》 (16)此海洋环流有科氏惯性力引起 地球 2 S4=-mak=-m(22×y,) 逆时针转动→在南半球 5 =2m2sino.v 圆周运动Sk=m R sino 2coso 所以2m2sinp·v,=m R 22sinp= R 又知:周期T= 2πR 8⑧-- 得兰=2 π sino= π Qsino π π 123 sin= To 16小时 2 16 =4 24小时 3 p=arcsin≈48.6 四、综合分析题(A) (17)对0轴的动量矩定理 lo+mrd小-in0 0=p+“1,0=0+”,6=0 所以 (18)(1+mr2)8+mgrsin0=0 (19)F-mgsine=mre M y 得F=mg sin0-,mr ↓mg mg I+mr2 mgsine (20)(1+mr2)8d0=-mgrsin6u0 (mgr sin ado I+mr2 条件:u≥1+mn 2mgr3 五、综合分析题(B) (21)系统自由度数3+1=4 5
当 W b c P ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ > µ + 时,hmin 取上值;当 W b c W P ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ µ < ≤ µ + 时,hmin = 0 。 (16) 此海洋环流有科氏惯性力引起 Ω Ω Ωsinϕ Ω cosϕ ϕ 地球 Ωsinϕ R ak r v k s ϕ (2 ) k mak m r s = − = − Ω × v 逆时针转动→在南半球 k r s = 2mΩ sinϕ ⋅ v 圆周运动 R v s m r k 2 = , 所以 R v m v m r r 2 2 Ω sinϕ ⋅ = , R vr 2Ω sinϕ = 又知:周期 r v R T 2π = , 得 R T vr 2π = , T π Ω sinϕ = 4 3 16 12 24 2 16 sin = = = = 小时 小时 π Ω π ϕ T , o 48.6 4 3 ϕ = arcsin ≈ 四、综合分析题(A) (17) 对 O 轴的动量矩定理 [ ] ϕ θ sinθ d d 2 I mr mgr t + = − & & θ ϕ θ ϕ θ ϕ&& && & & = + , = + , = r u t r u 所以 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + t r u mgr r u I mr t ϕ ϕ sin ϕ d d 2 & & ( ) sin 0 2 ⎟ = ⎠ ⎞ ⎜ ⎝ ⎛ + + + t r u I mr ϕ&& mgr ϕ (18) ( ) sin 0 2 I + mr θ + mgr θ = && (19) θ θ F mg mr && − sin = 得 sinθ sinθ sinθ 2 2 2 mg I mr I mg I mr mr F mg + = + = − M O θ ϕ y mg r M F θ N y mg r (20) (I mr )θdθ mgrsinθdθ 2 + = − & & ∫ ∫ + = − 2 0 0 2 ( ) sin π I mr θdθ mgr θdθ u r & & 2 3 2 2 I mr mgr u + = 条件: 2 3 2 I mr mgr u + ≥ 五、综合分析题(B) (21) 系统自由度数 3+1=4 5