
h=h先 E振=hv光=2πV4 hk 2πY4 1 V振=V光 v= 2πV4 2πc1V (2.15) 由(2.15)式看出:分子固有振动频率也就是它所能吸 收的辐射光的频率。 哈潮清黛大多 HARBIN LNTVERSITY OP COMMERCE
h k E hv 2 振 = 光 = h k hv hv 2 振 = 光 = k 2 1 v 振 = v 光 = k c v 2 ~ 1 = (2.15) 由(2.15)式看出:分子固有振动频率也就是它所能吸 收的辐射光的频率

任何分子的原子总是在围绕它们的平衡位置附近作 微小的振动,这些振动的振幅很小,而振动的频率却很 高(v=1013~1014Hz),正好和红外光的振动频率在同 一数量级。分子发生振动能级跃迁时需要吸收一定的能 量,这种能量通常可由照射体系的红外线供给。由于振 动能级是量子化的,因此分子振动将只能吸收一定的能 量,吸收能量后,从而使振动的振幅加大。这种吸收的 能量将取决于键力常数(k)与两端连接的原子的质量, 即取决于分子内部的特征。这就是红外光谱可以测定化 合物结构的理论依据。 给酒渭商業大是 HARBIN LNIVERSTTY OF COMMERCE
任何分子的原子总是在围绕它们的平衡位置附近作 微小的振动,这些振动的振幅很小,而振动的频率却很 高(v = 1013~1014Hz),正好和红外光的振动频率在同 一数量级。分子发生振动能级跃迁时需要吸收一定的能 量,这种能量通常可由照射体系的红外线供给。由于振 动能级是量子化的,因此分子振动将只能吸收一定的能 量,吸收能量后,从而使振动的振幅加大。这种吸收的 能量将取决于键力常数(k)与两端连接的原子的质量, 即取决于分子内部的特征。这就是红外光谱可以测定化 合物结构的理论依据
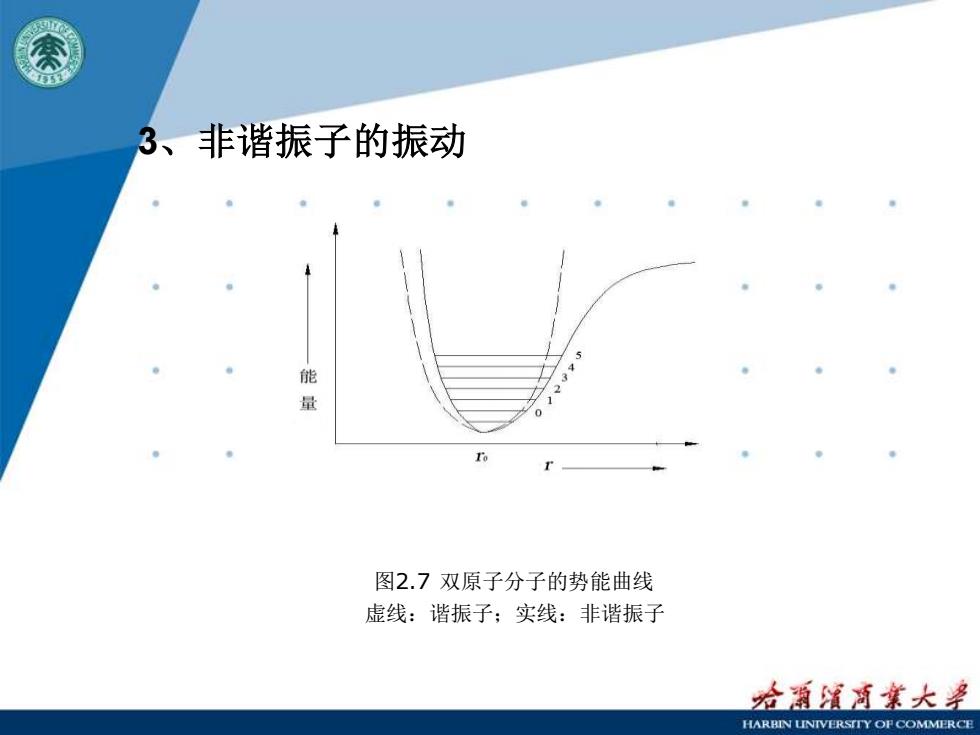
3、非谐振子的振动 能 量 图2.7双原子分子的势能曲线 虚线:谐振子;实线:非谐振子 疮潮清月業大孕 HARBIN LNTVERSITY OP COMMERCE
3、非谐振子的振动 图2.7 双原子分子的势能曲线 虚线:谐振子;实线:非谐振子

多原子分子的振动 。多原子分子由于组成原子数目增多,组成分子的键 或基团和空间结构的不同,其振动光谱比双原子分子要 复杂的多。但是可以把它们的振动分解成许多简单的基 本振动,即简正振动。 a简正振动 简正振动的状态是,分子的质心保持不变,整体不转 动,每个原子都在其平衡位置附近做简谐振动,其振动 频率和位相都相同,即每个原子都在同一瞬间通过其平 衡位置,而且同时达到其最大位移值。分子中任何一个 复杂振动都可以看成这些简正振动的线性组合。 宏酒演商業大圣 HARBIN LNIVERSTTY OF COMMERCE
4、多原子分子的振动 多原子分子由于组成原子数目增多,组成分子的键 或基团和空间结构的不同,其振动光谱比双原子分子要 复杂的多。但是可以把它们的振动分解成许多简单的基 本振动,即简正振动。 a 简正振动 简正振动的状态是,分子的质心保持不变,整体不转 动,每个原子都在其平衡位置附近做简谐振动,其振动 频率和位相都相同,即每个原子都在同一瞬间通过其平 衡位置,而且同时达到其最大位移值。分子中任何一个 复杂振动都可以看成这些简正振动的线性组合
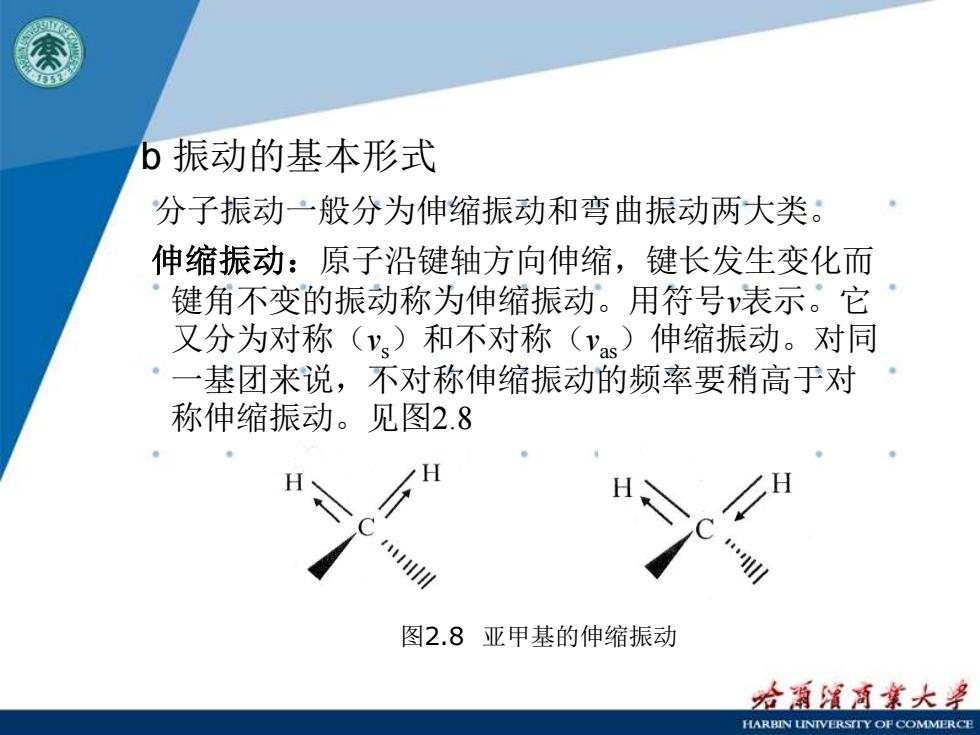
b振动的基本形式 分子振动一般分为伸缩振动和弯曲振动两大类。 伸缩振动:原子沿键轴方向伸缩,键长发生变化而 键角不变的振动称为伸缩振动。用符号v表示。它 又分为对称(ys)和不对称(vas)伸缩振动。对同 ·一基团来说,不对称伸缩振动的频率要稍高于对 称伸缩振动。见图2.8 图2.8亚甲基的伸缩振动 疮潮清月業大孕 HARBIN LNTVERSITY OF COMMERCE
b 振动的基本形式 分子振动一般分为伸缩振动和弯曲振动两大类。 伸缩振动:原子沿键轴方向伸缩,键长发生变化而 键角不变的振动称为伸缩振动。用符号v表示。它 又分为对称(vs)和不对称(vas)伸缩振动。对同 一基团来说,不对称伸缩振动的频率要稍高于对 称伸缩振动。见图2.8 图2.8 亚甲基的伸缩振动