
3.精密度的量度 r偏差(deviation 正值或负值 ☆绝对偏差d: d =x,-X 矿平均偏差 ☆平均偏差d (绝对) d-k +d3+.+d。 n ☆相对平均偏差: a-x100% d x 上一页下一页返回退出
上一页 下一页 返回 退出 3. 精密度的量度 偏差(deviation ) 绝对偏差di: 平均偏差 (绝对): 相对平均偏差: d x x i = i − d n d d d d n + ++ = 1 2 = 100% x d dr 返回 正值或负值 平均偏差

©标准偏差 (均方根偏差) 4一总体 平均值 ☆总体标准偏差σ: ☆n趋于无限次时, ∑(x-4)}月 ☆样本标准偏差§: f=n-1, ∑(x-x羽 自由度 ◇n为有限次时, n-1 ☆相对标准偏差RSD或变异系数CV: S RSD=二×100% x 上一页下一页返回退出
上一页 下一页 返回 退出 标准偏差(均方根偏差) 总体标准偏差: n趋于无限次时, 样本标准偏差s: n为有限次时, 相对标准偏差RSD或变异系数CV: n xi − = 2 ( ) 1 ( ) 2 − − = n x x s i f = n-1, 自由度 = 100% x s RSD 返回 -总体 平均值
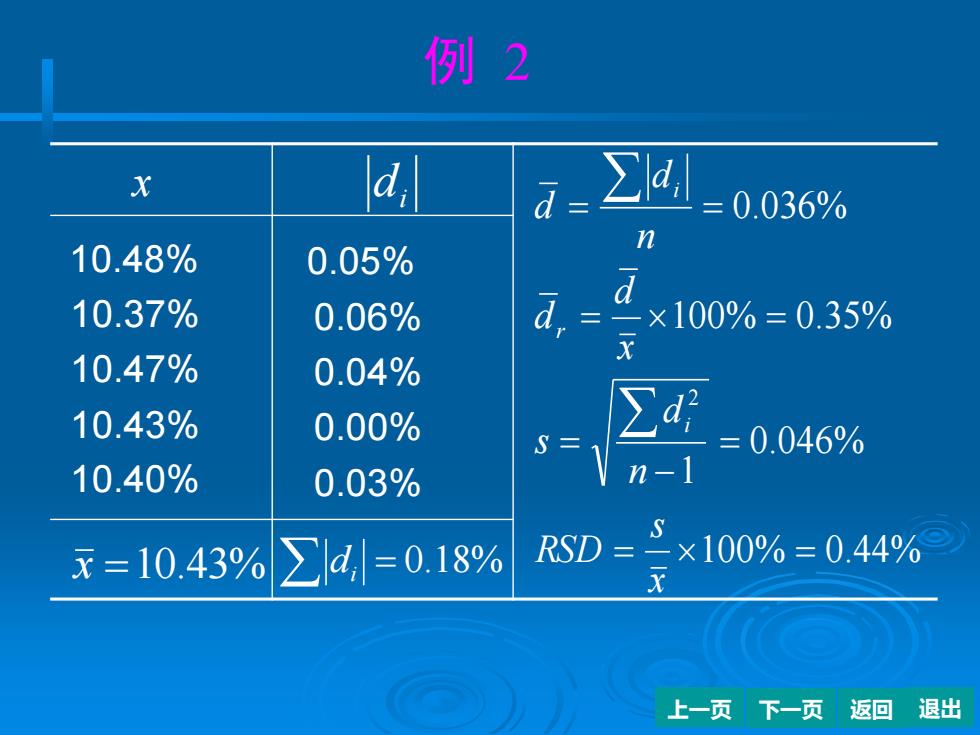
例2 x 0.036% n 10.48% 0.05% d 10.37% 0.06% d,=×100%=0.35% 10.47% 0.04% 10.43% 0.00% =0.046% 10.40% 0.03% n-1 S x=10.43% ∑d=0.18% RSD=2x100%=0.44% 上一页下一页返回退出
上一页 下一页 返回 退出 例 2 x 10.48% 10.37% 10.47% 10.43% 10.40% 0.05% 0.06% 0.04% 0.00% 0.03% x =10.43% di di = 0.18% 100% 0.44% 0.046% 1 100% 0.35% 0.036% 2 = = = − = = = = = x s RSD n d s x d d n d d i r i 返回
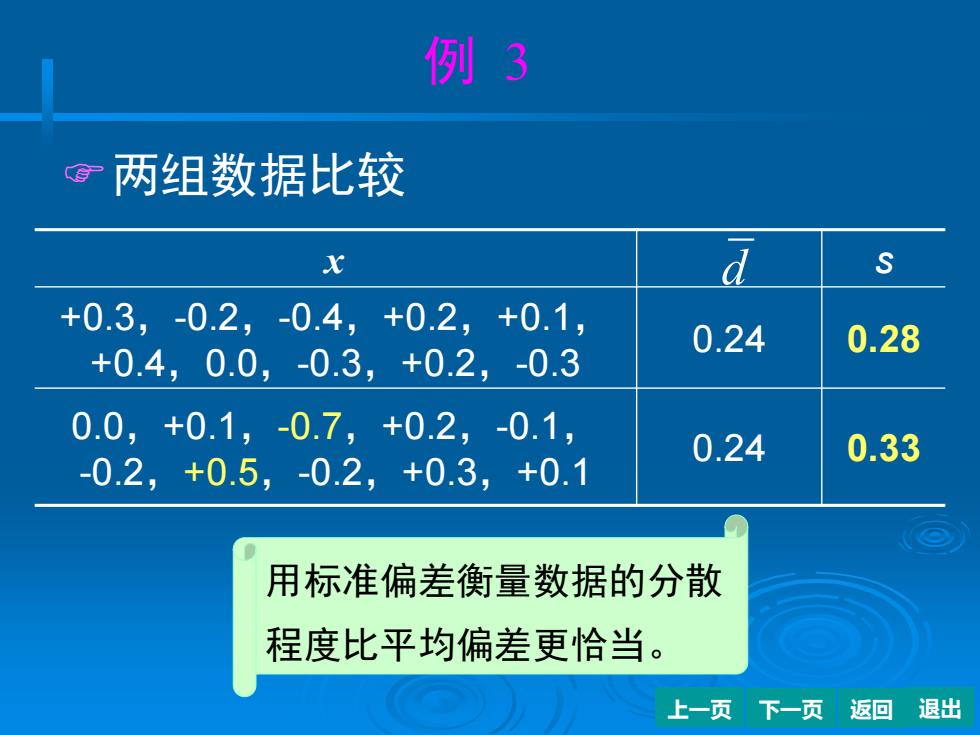
例3 G 两组数据比较 x a S +0.3,-0.2,-0.4,+02,+0.1, 0.24 0.28 +0.4,0.0,-0.3,+0.2,-0.3 0.0,+0.1,-0.7,+0.2,-0.1, 0.24 0.33 -0.2,+0.5,-02,+0.3,+0.1 用标准偏差衡量数据的分散 程度比平均偏差更恰当。 上一页下一页返回退出
上一页 下一页 返回 退出 例 3 两组数据比较 x s +0.3,-0.2,-0.4,+0.2,+0.1, +0.4,0.0,-0.3,+0.2,-0.3 0.24 0.28 0.0,+0.1,-0.7,+0.2,-0.1, -0.2,+0.5,-0.2,+0.3,+0.1 0.24 0.33 d 返回 用标准偏差衡量数据的分散 程度比平均偏差更恰当

4.准确度和精密度关系 甲二者均好 乙精密度好 丙二者皆不好 24.05%24.15%24.25%24.35%24.45% 真值 结论:精密度是保证准确度的先决条件! 上一页下一页返回退出
上一页 下一页 返回 退出 4. 准确度和精密度关系 结论:精密度是保证准确度的先决条件! 二者均好 精密度好 二者皆不好 ???? 甲 乙 丙 真值 24.05% 24.15% 24.25% 24.35% 24.45% 丁