华东师范大学：《高等数值分析（高性能计算/并行计算）》课程教学资源（讲义）10 二维Poisson方程的并行求解算法（基于MPI）

華束师免天学|数学科学学院 School of Mathematical Sciences.East China Normal University 二维Poisson方程的 并行求解算法 (基于MPI) http://math.ecnu.edu.cn/~jypan

http://math.ecnu.edu.cn/~jypan 1 二维 Poisson 方程的 并行求解算法 （基于MPI）

华东师范大学数学科学学院 目录页 School of Mathematical Sciences,ECNU Contents 问题的离散 2 Jacobi算法及并行实现 3 基于红黑排序的并行GS算法 http://math.ecnu.edu.cn/~jypan

http://math.ecnu.edu.cn/~jypan 目录页 Contents 华东师范大学 数学科学学院 School of Mathematical Sciences, ECNU http://math.ecnu.edu.cn/~jypan 1 2 问题的离散 Jacobi 算法及并行实现 3 基于红黑排序的并行 GS 算法

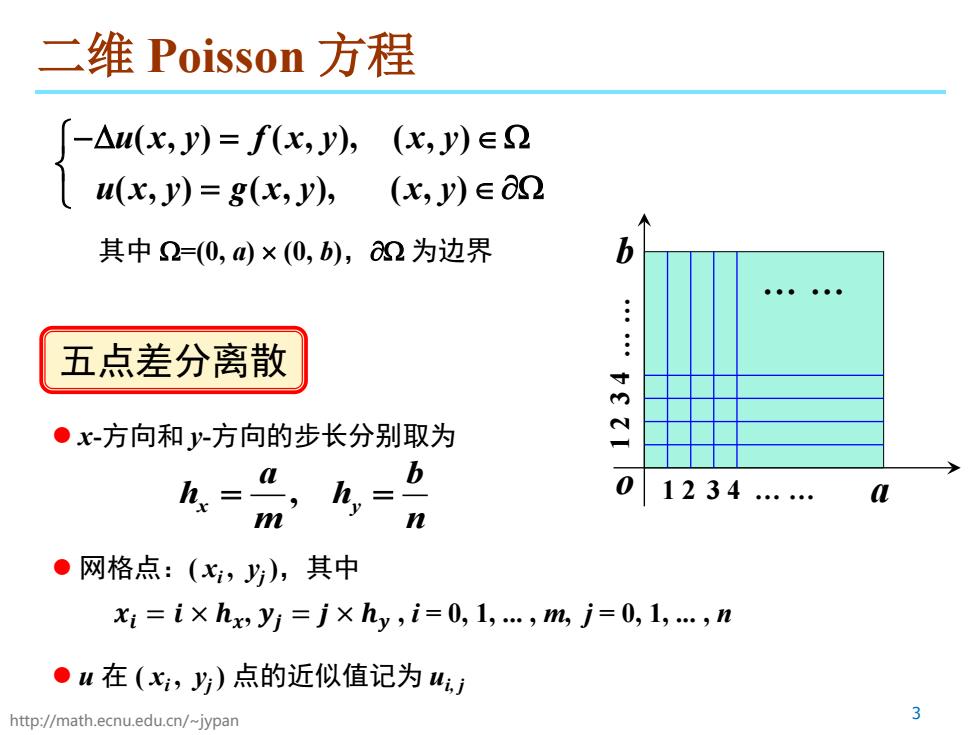
二维Poisson方程 -△u(x,y)=f(x,y) (x,y)∈2 (x,y)=g(x,y), (x,y)∈O2 其中2=(0，)×(0，b),2为边界 b 五点差分离散 ●x-方向和y-方向的步长分别取为 h=a, 1234 L n ●网格点：（x,),其中 xi=i×hx,yj=j×hy,i=0,1,…,m,j=0,1,…,n ●W在(，y)点的近似值记为 http://math.ecnu.edu.cn/~jypan 3

http://math.ecnu.edu.cn/~jypan 3 二维 Poisson 方程 ( , ) ( , ), ( , ) ( , ) ( , ), ( , ) uxy f xy xy uxy gxy xy −∆ = ∈ Ω   = ∈ ∂Ω 其中 Ω=(0, a) × (0, b)，∂Ω 为边界 o a b … … 1 2 3 4 … … 1 2 3 4 … …  x-方向和 y-方向的步长分别取为 , x y a b h h m n = =  网格点：( xi , yj )，其中 𝒙𝒙𝒊𝒊 = 𝒊𝒊 × 𝒉𝒉𝒙𝒙, 𝒚𝒚𝒋𝒋 = 𝒋𝒋 × 𝒉𝒉𝒚𝒚 , i = 0, 1, ... , m, j = 0, 1, ... , n  u 在 ( xi , yj ) 点的近似值记为 ui, j 五点差分离散

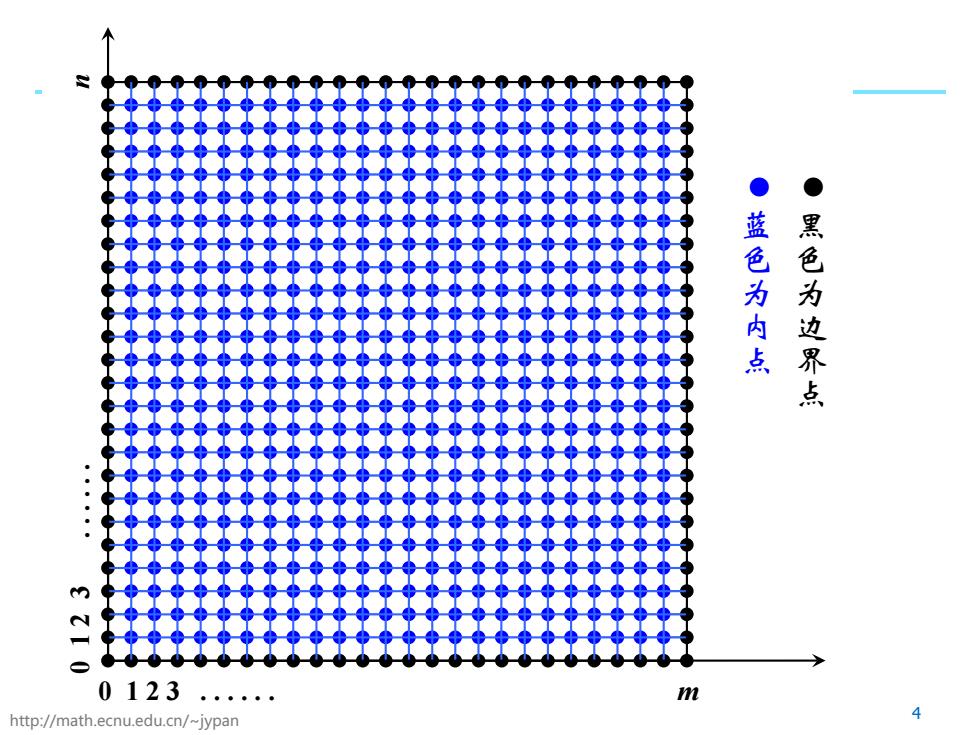
● ● 蓝色为内点 黑色为边界点 0123 m http://math.ecnu.edu.cn/~jypan 4

http://math.ecnu.edu.cn/~jypan 4 0 1 2 3 . . . . . . m 0 1 2 3 . . . . . . n  蓝色为内点  黑色为边界点

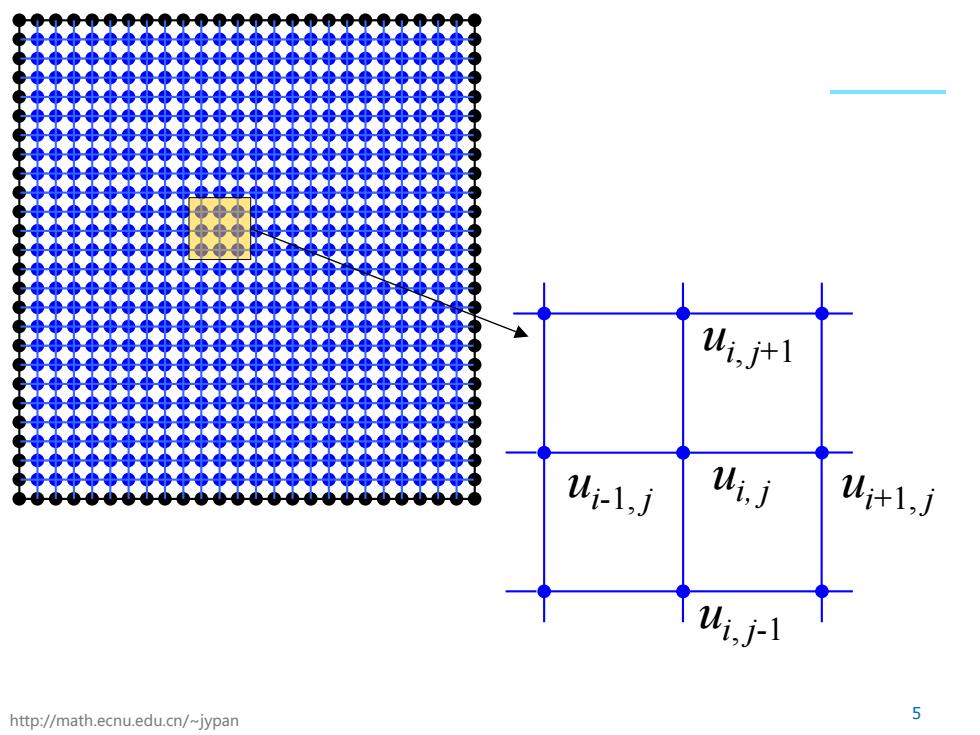
Ui,j计1 Ui-1,j Wi,j 认t1,j Ui,j- http://math.ecnu.edu.cn/~jypan 5

http://math.ecnu.edu.cn/~jypan 5 ui, j ui, j-1 ui+1, j ui, j+1 ui-1, j