
Which expert to follow? Each day,stock market goes up or down. TRUSSKEY FINANCIAL ADVISORS Let's Talk Investing N小d HERB WHITE TIAHOME.COM (936)588-0288 At the end of the day,we'll see whether the market actually goes up or down. We lose 1 if our prediction was wrong. 6
Which expert to follow? ◼ Each day, stock market goes up or down. ◼ At the end of the day, we’ll see whether the market actually goes up or down. ◼ We lose 1 if our prediction was wrong. 6

After a year,we'll see with hindsight that one expert is the best. But,of course,we don't know who in advance. nWe''ll think“'If we had followed his advice.” Theorem:We have a method to perform close to the best expert! We don't assume anything about the experts. They may not know what they are talking about They may even collaborate in any bad manner
◼ After a year, we’ll see with hindsight that one expert is the best. ❑ But, of course, we don’t know who in advance. ◼ We’ll think “If we had followed his advice…” ◼ Theorem: We have a method to perform close to the best expert! ❑ We don’t assume anything about the experts. ◼ They may not know what they are talking about. ◼ They may even collaborate in any bad manner. 7

Method and intuition Algorithm:Randomized Weighted Majority Use random choice:following expert i with probability pi If an expert predicts wrongly:punish him by decreasing the probability of choosing him/her in next round. If someone gives you wrong info,then you tend to trust him less in future. 8
Method and intuition ◼ Algorithm: Randomized Weighted Majority ◼ Use random choice: following expert 𝑖 with probability 𝑝𝑖 ◼ If an expert predicts wrongly: punish him by decreasing the probability of choosing him/her in next round. ❑ If someone gives you wrong info, then you tend to trust him less in future. 8

Randomized Weighted Majority w:weight of experti at time :probability of choosing expertiat time for each i∈[n] w0=1,p=1/m for each t>1,i∈[n]: if expert i was wrong at step t-1 w0=w-(1-e) else Decrease your weight! w=w-0 op40=w0/∑w0 Probability is proportional to weight Choose i with prob.p and follow expert i's advice. 9
Randomized Weighted Majority ◼ for each 𝑖 ∈ [𝑛] 𝑤𝑖 (1) = 1, 𝑝𝑖 (1) = 1/𝑛 ◼ for each 𝑡 > 1, ∀𝑖 ∈ [𝑛]: ❑ if expert 𝑖 was wrong at step 𝑡 − 1 𝑤𝑖 (𝑡) = 𝑤𝑖 (𝑡−1) (1 − 𝜀) else 𝑤𝑖 (𝑡) = 𝑤𝑖 (𝑡−1) ❑ 𝑝𝑖 (𝑡) = 𝑤𝑖 𝑡 /σ𝑖 𝑤𝑖 (𝑡) ❑ Choose 𝑖 with prob. 𝑝𝑖 (𝑡) , and follow expert 𝑖’s advice. 𝑤𝑖 (𝑡) : weight of expert 𝑖 at time 𝑡 𝑝𝑖 (𝑡) : probability of choosing expert 𝑖 at time 𝑡 Decrease your weight! Probability is proportional to weight 9
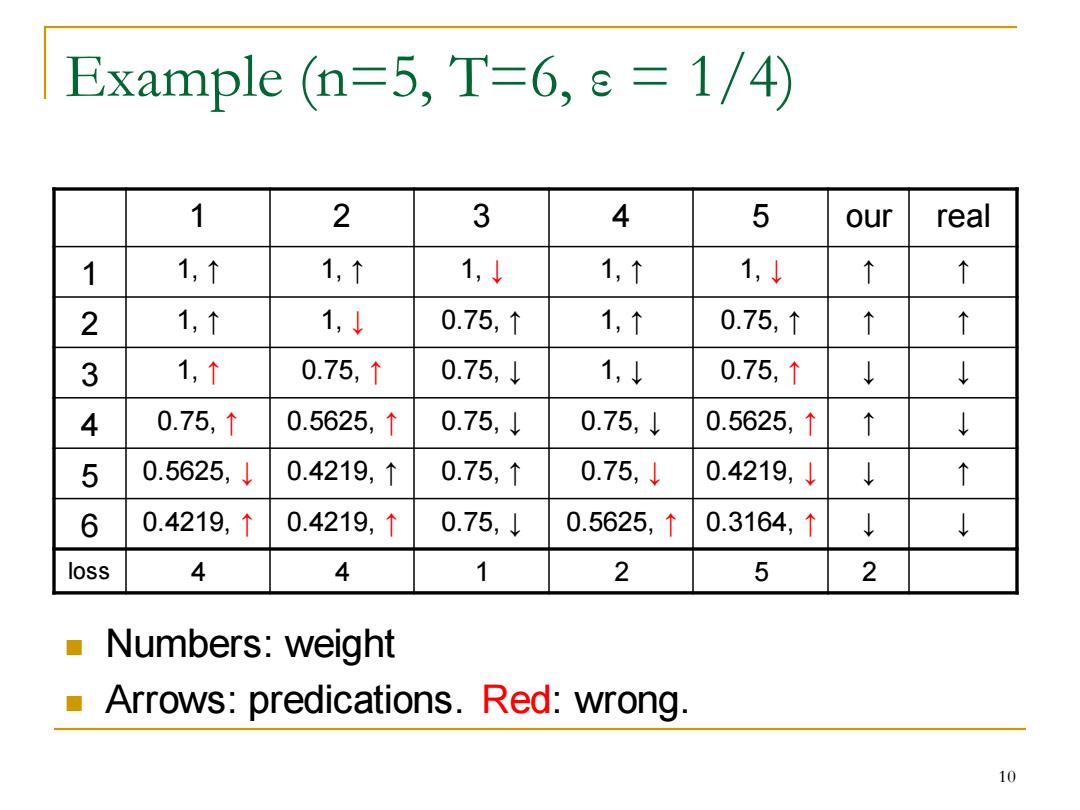
Example (n=5,T=6,e=1/4) 1 2 3 4 5 our real 1 1,↑ 1,↑ 1,↓ 1,↑ 1,↓ ↑ 2 1,↑ 1, 0.75,↑ 1,↑ 0.75,↑ 个 3 1,↑ 0.75,↑ 0.75,↓ 1,↓ 0.75,↑ ↓ 4 0.75,↑ 0.5625,↑ 0.75,↓ 0.75,↓ 0.5625,↑ 5 0.5625,↓ 0.4219,↑ 0.75,↑ 0.75,↓ 0.4219,↓ 6 0.4219,↑ 0.4219,↑ 0.75,↓ 0.5625,↑ 0.3164,↑ ↓ loss 4 4 1 2 5 2 Numbers:weight Arrows:predications.Red:wrong. 10
Example (n=5, T=6, ε = 1/4) 1 2 3 4 5 our real 1 1, ↑ 1, ↑ 1, ↓ 1, ↑ 1, ↓ ↑ ↑ 2 1, ↑ 1, ↓ 0.75, ↑ 1, ↑ 0.75, ↑ ↑ ↑ 3 1, ↑ 0.75, ↑ 0.75, ↓ 1, ↓ 0.75, ↑ ↓ ↓ 4 0.75, ↑ 0.5625, ↑ 0.75, ↓ 0.75, ↓ 0.5625, ↑ ↑ ↓ 5 0.5625, ↓ 0.4219, ↑ 0.75, ↑ 0.75, ↓ 0.4219, ↓ ↓ ↑ 6 0.4219, ↑ 0.4219, ↑ 0.75, ↓ 0.5625, ↑ 0.3164, ↑ ↓ ↓ loss 4 4 1 2 5 2 ◼ Numbers: weight ◼ Arrows: predications. Red: wrong. 10