Equivalence of Criteria:R is generated by B R B(v) P 3 L PPA Section 4.1 C F.Nielson H.Riis Nielson C.Hankin (Dec.2004) 11
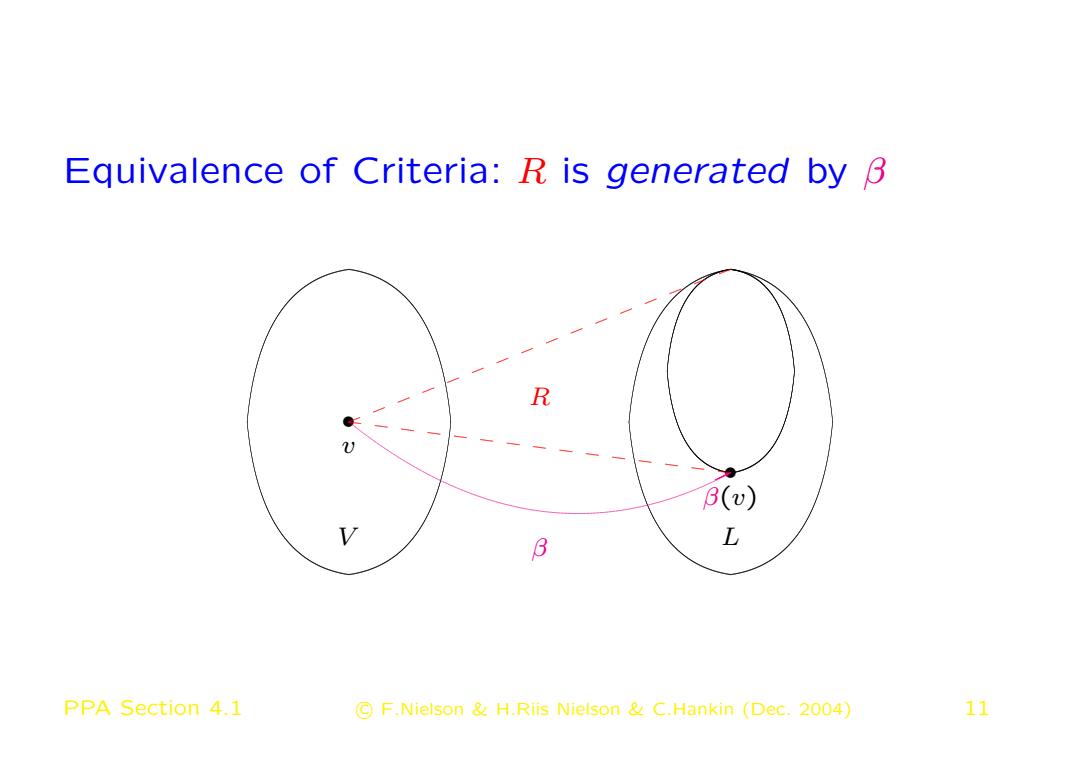
Equivalence of Criteria: R is generated by β • v V • β(v) L R ✟✟✯ β PPA Section 4.1 c F.Nielson & H.Riis Nielson & C.Hankin (Dec. 2004) 11

Example:Data Flow Analysis Representation function Bcp:State→Statecp is defined by Bcp(o)=λx.o(x) Rcp is generated by Bcp: o Rcp iff BCP(o)EcP PPA Section 4.1 C F.Nielson H.Riis Nielson C.Hankin (Dec.2004) 12
Example: Data Flow Analysis Representation function βCP : State → State d CP is defined by βCP(σ) = λx.σ(x) RCP is generated by βCP: σ RCP σb iff βCP(σ) vCP σb PPA Section 4.1 c F.Nielson & H.Riis Nielson & C.Hankin (Dec. 2004) 12

Example:Control Flow Analysis Representation function cFA:Val→Env x Val is defined by (入x.0,0) if v=c BcA@=了(片A(p),t)ifu=clo8etnp A(p)()=Upy()IBCFA(p(y))=(Py,u)and yedom(p)} {8} if xE dom(p)and BCFA(p())=(pa, otherwise RCFA is generated by BCFA: RCFA (p,)iff BCFA()ECFA (P,) PPA Section 4.1 C F.Nielson H.Riis Nielson C.Hankin (Dec.2004) 13
Example: Control Flow Analysis Representation function βCFA : Val → Env d × Val d is defined by βCFA(v) = ( (λx.∅, ∅) if v = c (β E CFA(ρ), {t}) if v = close t in ρ β E CFA(ρ)(x) = [ {ρby(x) | βCFA(ρ(y)) = (ρby, vby) and y ∈ dom(ρ)} ∪ ( {vbx} if x ∈ dom(ρ) and βCFA(ρ(x)) = (ρbx, vbx) ∅ otherwise RCFA is generated by βCFA: v RCFA (ρb, vb) iff βCFA(v) vCFA (ρb, vb) PPA Section 4.1 c F.Nielson & H.Riis Nielson & C.Hankin (Dec. 2004) 13

A Modest Generalisation Semantics: Program analysis: p卜v1v2 p-l112 where v1∈Vi,v2∈V2 where l1∈L1,l2∈L2 p卜 Ul U2 logical relation: Ri → R2 (p卜·→)(R1R2)(pFD) P人 l 12 PPA Section 4.1 C F.Nielson H.Riis Nielson C.Hankin (Dec.2004) 14
A Modest Generalisation Semantics: p ` v1 ❀ v2 where v1 ∈ V1, v2 ∈ V2 Program analysis: p ` l1 ✄ l2 where l1 ∈ L1, l2 ∈ L2 p ` v1 ❀ v2 ... ... R1 ⇒ R2 ... ... p ` l1 ✄ l2 logical relation: (p ` · ❀ ·) (R1 →→ R2) (p ` · ✄ ·) PPA Section 4.1 c F.Nielson & H.Riis Nielson & C.Hankin (Dec. 2004) 14

Higher-Order Formulation Assume that R1 is an admissible correctness relation for Vi and L1 that is generated by the representation function B1:Vi-L1 R2 is an admissible correctness relation for v2 and L2 that is generated by the representation function B2:V2-L2 Then the relation R1-R2 is an admissible correctness relation for V1→V2andL1→L2 that is generated by the representation function B132 defined by (B1B2)()=λl1☐{32(v2)|31(v1)El1∧v1w2} PPA Section 4.1 F.Nielson H.Riis Nielson C.Hankin (Dec.2004) 15
Higher-Order Formulation Assume that • R1 is an admissible correctness relation for V1 and L1 that is generated by the representation function β1 : V1 → L1 • R2 is an admissible correctness relation for V2 and L2 that is generated by the representation function β2 : V2 → L2 Then the relation R1 →→ R2 is an admissible correctness relation for V1 → V2 and L1 → L2 that is generated by the representation function β1 →→ β2 defined by (β1 →→ β2)(❀ ) = λl1. G {β2(v2) | β1(v1) v l1 ∧ v1 ❀ v2} PPA Section 4.1 c F.Nielson & H.Riis Nielson & C.Hankin (Dec. 2004) 15