
1.2流体静力学 9 有了连续介质假设,我们对流体的宏观性质的描述应该是,流体是均匀的连续体,而不是 含有大址分子的离散体。流体流动是流体质点的位移,而不是个别分子的位移。研究流体静 力学时,流体质点是静止不动的,虽然其中的分子热运动在不断进行。 1.1.3流体的易流动性和粘性 固体在静止时它的界面上可以承受切应力,固体沿界面切线方向发生微小的形变,而后达 到平衡,界面上承受着切应力。这说明固体在静止时既能承受法应力也能承受切应力。而流 体静止时只要持续施加切应力,都能使流体流动,发生任意大的形变,这种流体的宏观性质称 为易流动性。它说明流体静止时,只有法应力没有切应力。 流体在静止时虽不能承受切应力,但在运动时却对两层流体间的相对运动,即相对滑动速 率有抵抗。流体的这种抵抗两层流体相对滑动速率即抵抗形变的性质称作粘性,也称内摩擦 力。 当流体的粘性很小时,比如空气和水在运动速率不大时,所产生的粘性应力比起惯性力等 可忽略不计时,我们可近似地把它看成是无粘性的,称作理想流体。对粘性应力不可忽路的称 为粘性流体。理想流体在客观实际中是不存在的,它只是实际流体在某种条件下的近似模型。 1.1.4定态流动和非定态流动 流体流动空间各点的状态不随时间变化的流动称为定态流动。定态流动空间的任一固定 点,随着时间的流逝流体质点不断更新,但该点的运动参数(如压强、温度和流速等)不随时间 变化,系统的参数可随位置变化。相反,流体流动空间固定点的运动参数,随时间变化的流动 称为非定态流动。工业规模生产中连续运转的流动体系多为定态流动。 要注意定态性和稳定性是两个不同的概念,定态性指的是有关运动参数随时间的变化情 况。而稳定性则是指系统对外界干扰的反应,当系统受到瞬时扰动,使之偏离平衡状态,而扰 动消失后,它能自动恢服原平衡状态,则该平衡状态是稳定的。反之,则不稳定。例如后面要 学到的层流区的层流平衡状态的稳定性和反应器的热稳定性。 1.2流体静力学 流体静力学是研究流体在外力作用下达平衡,处于静止状态的规律。流体静力学基本方 程在工程实践中,应用很广泛。 1.2.1流体的密度 流体的密度p为单位体积流体的质量,法定单位为kg·m3。由于流体具有压缩性,一定 质址流体的体积要随温度、压力的变化而变化,即流体密度要随温度、压力变化。 液体密度基本上不随压力变化,随温度略有变化,手册上可查到。在工程计算中,带把液 体密度视为常数。 气体的密度随温度和压力的变化而变化。在压力不太高、温度不太低时,从手册上查得的 某指定条件下的密度,可按理想气体状态方程进行换算。 流体的密度在传递工程中也称为质量浓度。密度的倒数称为比体积,单位为m3·kg'。 化学工业过程处理的流体物料常常是混合物。液体混合物的平均密度Pm,在工程计算中

10 第1章流体的流动及输送 可忽略偏摩尔体积的影响,近似按下式计算: =宫兴 (1-1) 式中:w,一液体混合物中i组分的质量分数:,一液体混合物中i组分的密度。 气体混合物的平均密度用下式计算: Pm-0 (1-2) 式中: ,一气体混合物中:组分的体积分数。 若气体混合物可按理想气体处理,气体混合物的平均摩尔质量Mm用下式计算: Mm=∑Moy (1-3) 式中:M,一混合物气体中组分的摩尔质量:一混合物气体中i组分的摩尔分数。 则气体混合物的密度,用理想气体状态方程计算: Pm=RT (1-4) 1.2.2流体的静压强 压力是法向表面力,表面力是接触力与表面积成正比。单位面积上所受的压力称为压强。 在静止流体内,过任一点取任意界面其面积为△A,垂直作用于该面积上的压力为F,单位面 积上所受的压力称为流体的静压强 =AA (1-5) 式中:币为所取界面的平均静压强。 p=典后 (1-6) 式中:力为该点的静压强。 如前所述,流体具有易流动性,静止流体任意界面上只承受大小相等方向相反的静压力, 不存在切向力。 静压强的法定单位是N:m2,即Pa(帕[斯卡])。与历史上曾用过以往资料中常见的物理 大气压(atm)、工程大气压(1at=1kgf·cm2)、毫米汞柱(mmHg)、米水柱(mH,O)、巴(bar)等 压强单位间的关系如下: 1atm=1.0133×105Pa=1.0133bar=760mmHg=10.33mlH,0=1.033 kgf-cm2 1at=1kgcm2=735.6mmHg=10mH20=0.9807×103Pa=0.9807bar 式中:kgf称为公斤力,是历史上工程单位制的基本单位。1kg是质量为1kg的物质在重力加 速度为9.807ms2所受的重力。 1kgf=1kg×9.807ms2=9.807N 在工程上,压强有不同的基准不同的术语。绝对压强是以绝对零压为基准,表示流体的真 实压强。表压是以大气压强为基准,高出大气压强的数值,由压强表测定读数。真空度是以大 气压为基准,低于大气压强的数值,由真空表测得。其关系见图11,关系式如下: 表压强=绝对压强一大气压强 真空度=大气压强一绝对压强
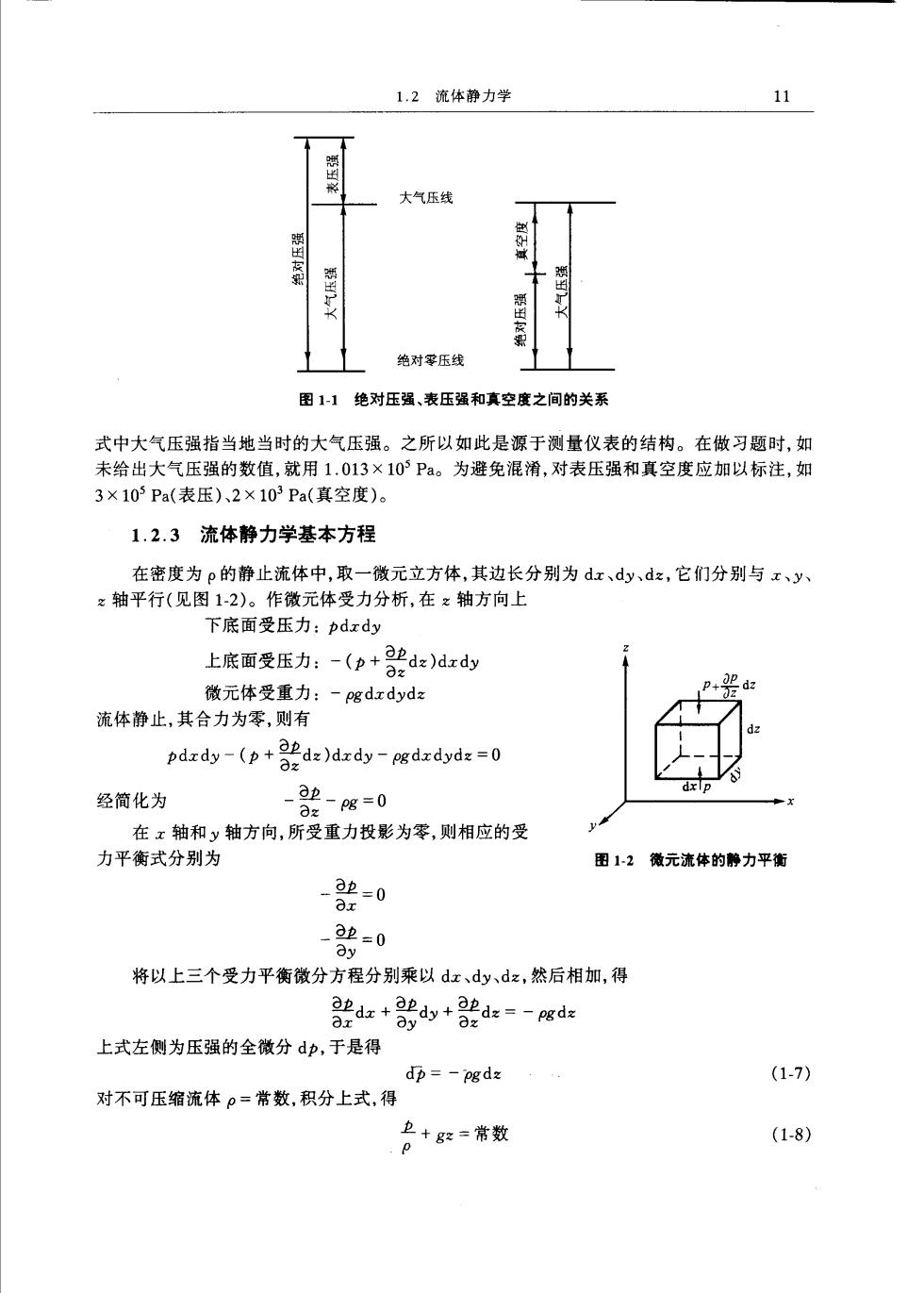
1.2流体静力学 11 大气压线 绝对压线 图1-1绝对压强、表压强和真空度之间的关系 式中大气压强指当地当时的大气压强。之所以如此是源于测量仪表的结构。在做习题时,如 未给出大气压强的数值,就用1.013×10P。为避免混滑,对表压强和真空度应加以标注,如 3×103Pa(表压)、2×103Pa(真空度)。 1.2.3流体静力学基本方程 在密度为p的静止流体中,取一微元立方体,其边长分别为dx、dy、dz,它们分别与x、y x轴平行(见图12)。作微元体受力分析,在z轴方向上 下底面受压力:pdxdy 上底面受压力:-(p+驶dx)ardy 微元体受重力:-pgdxdydz 流体静止,其合力为零,则有 pdxdy-(d)dxdyddyd0 经简化为 _22-0g=0 在x轴和y轴方向,所受重力投影为零,则相应的受 力平衡式分别为 里12微元流体的静力平衡 -82=0 2=0 oy 将以上三个受力平衡微分方程分别乘以dx、dy、dz,然后相加,得 82dr+的dy+32dx=-pgd 上式左侧为压强的全微分dp,于是得 db=-ogdz (1-7) 对不可压缩流体ρ=常数,积分上式,得 +8常数 (1-8)

、12 第1章流体的流动及输送 在静止液体内取1、2两点(见图13) (1-9) P2=p1+Pg(z1-2) 若将1点取在液面上,液面上方压强为p,被体内部任一点的 图1-3静止液体内的压强分布 压强为力,则 =pu+pgh (1-10) 式中:h为该点离液面的垂直距离,即该点上方的液柱高。 式(1-8) (1-10)称为重力场中流体静力学基本方程,是静止液体内压强分布规律。该方 程仅适用于重力场中静止的不可压缩流体。液体近似为不可压缩流体,气体虽具有较大压缩 性,但在化工容器里其密度的变化可忽略,故上式也适用于气体,所以统称为流体静力学方程。 由流体静力学方程可得,当液面上方压强一定时,静止液体内部任一点的压强仅与液体的 密度和该点上方的液柱高有关,从而得出,在静止的连续的同一液体内,同一水平面上各点的 压强相等,与容器形状无关 图14所示为4个形状不同,但底面积(为A)相等的容器,当其中盛有等高度h的水时, 理论和实验均表明其底面所受的压力均为(po+Pgh)A。显然,它与固体截然不同,这就是著 名的流体静力学矛盾。通过对该例的分析思考不难得出结论,流体中各质点间的相对位置可 以改变,是它与固体的重要区别,由此形成了流体运动的特有规律。 (a) (b) 图14几种形状不同(底面积相等)的容器 1.2.4流体静力学基本方程的应用 (一)压强的测量 以流体静力学基本方程为依据的测压仪器称为液柱压差计。主要有以下两种: 1.U型压差计 U型压差计的结构如图15所示,它是一根U型玻璃管,内装指 示液A,指示液不与被测流体B互溶,指示液的密度PA大于被测流 体的体度。m 当测量管道中1一1'与2一2两截面间流体的压强差时,将U管 两端口与测压口相连通。由于p1和p2不相等,压差计内指示液出 现高度差R。a,a是管内静止、连续、同一液体内等高的两点,故压 强相等,p.=p,即 PI+PBg(m+R)=p2+pBg(z+m)+PAgR 则 图15U型压差计 P1-P2=(PA-PB)gR+pBgz (1-11) 当被测压强处等高z=0

1.2流体静力学 13 P1-p2=(PA-PB)gR (1-12) 当被测流体是气体,且pB《PA P1-P2=PAgR (1-13) 要测某点的压强时,将U型压差计另一端口通大气。若被测压强高于大气压强,它就是 压强表。若被测压强低于大气压强,就是真空表。当压强差较大时选用密度大的指示液,如 Hg和CCL,等,当压强差较小时,要选用密度小的指示液如水等,可提高压差计读数精度。注 意,水银压差计开口端要注入一小段水,避免汞蒸气污染环境 【例11】采用串联U型压差计(指示液为汞)测量输 水管路A截面处的压强,见图1-6,其中R1=0.6m, R2=0.7m,h1=0.5m,h2=0.8m。两U管连接管充满水 当地大气压强o=9.807×104Pa。试求测得的压强。 解由静力学方程知 p1=p1=po+P粟gR2 p1=p2十P水gh2=p2十P水gh? p=p3=p的=p2+PgR1 p=P水gh1+p3 图16串联压差计 解得 p-po=0g(R1+R2)+g(h1-h2) =13600kgm-3×9.81ms2×(0.6+0.7)m-1000kgm3 ×9.81ms2×(0.8-0.5)m =1.705×103Pa(表压) 由本例可看出,把各参数联系在算式中的是“在静止的连缕的同一液体内等高处压强相 等“这一原理。另外它提示我们若压强差较大,为便于读数,可串联成复式U型压差计使用。 2.微压差计 若压强差很小,又要精确读出R值。人们就设计出双液杯式微压差计,如图17所示。U 管上端各装一扩大室,扩大室直径D与U管直径d之比要大于10。压 差计内装有A,C两种指示液,两者密度Pa和Pc相近,互不相溶不起反 应,也不与被测流体互溶。因为D/d>10,由R变化引起的扩大室内液 面变化很小,可视为等高,则压强差 P1-p2=(pA-pc)gR (1-14) 式中(PA-pC)值小,则R值大。即小的压强差,也可精确读取R值。通 常用它测气体的压强差。 例如要测的压强差△p=120Pa,若用苯(P苯=879kg°m3)作指示液 的U型压差计测量,压差计读数: R=0=879kgm 120P 9.81m*57=0.014m=14mm 图1-7徽压差计若用苯和水(ρ=998kg·m3)做指示液的双液杯式压差计测量,压差计读 数: