
U K 59.2两端铰支细长压杆的临界压力 两端铰支杆受压 力P作用 考察微弯平衡状态 x处截面的弯矩 (x) M=-Pv 挠曲线近似微分 方程 M dx2 EI 7一为截面最小的惯性矩 d2v Pv dx2 EI
7 §9. 2 两端铰支细长压杆的临界压力 两端铰支杆受压 力P作用 考察微弯平衡状态 x处截面的弯矩 M = −Pv 挠曲线近似微分 EI M x v = 2 2 d d I ⎯ 为截面最小的惯性矩 EI Pv x v = − 2 2 d d 方程 + v = 0 EI P v

D1) dx EI EI 引入记号 k2 EI v"+k2v=0 通解为 v=Asin kx+Bcoskx 其中,A、B为积分常数,由边界条件确定。 边界条件为:x=0时,v=0: x=1时,y=0 将x=0,y=0代入通解 B=0 将x=L,v=0代入通解 Asin kl=0
8 EI Pv x v = − 2 2 d d + v = 0 EI P v EI P k = 引入记号 2 0 2 v + k v = 通解为 v = Asin kx+ Bcoskx 其中,A、B为积分常数,由边界条件确定。 边界条件为: x = 0 时, v = 0; x = l 时, v = 0 将 x = 0, v = 0 代入通解 B = 0 将 x = l, v = 0代入通解 Asin kl = 0

UD 边界条件为:x=0时,v=0; x=1时,v=0 将x=0,v=0代入通解 B=0 将x=,v=0代入通解 Asin kl=0 因A≠0, 所以应有 sin kl=0 kl=nπ,(n=0,1,2, 代入2= n2元2El 12 因为临界压力是微弯平衡状态下的最 小压力,所以,应取n=1。 9
9 边界条件为: x = 0 时, v = 0; x = l 时, v = 0 将 x = 0, v = 0 代入通解 B = 0 将 x = l, v = 0 代入通解 Asin kl = 0 因 A 0, 所以应有 sin kl = 0 k l = n, (n = 0,1, 2, ) 代入 EI P k = 2 2 2 2 l n EI P = 因为临界压力是微弯平衡状态下的最 小压力,所以,应取 n = 1

U K 代入k2= n2π2E1 12 因为临界压力是微弯平衡状态下的最 小压力,所以,应取n=1。 元2E1 欧拉公式 12 这就是两端铰支细长压杆的临界压力公式。 当取n=1时,由kl=n元,→k= 则,挠曲线方程为v=Asim 元X 1 10
10 代入 EI P k = 2 2 2 2 l n EI P = 因为临界压力是微弯平衡状态下的最 小压力,所以,应取 n = 1 。 2 2 l EI Pcr = 这就是两端铰支细长压杆的临界压力公式。 ⎯ 欧拉公式 当取 n = 1 时,由 kl = n, l k = 则,挠曲线方程为 l x v A = sin
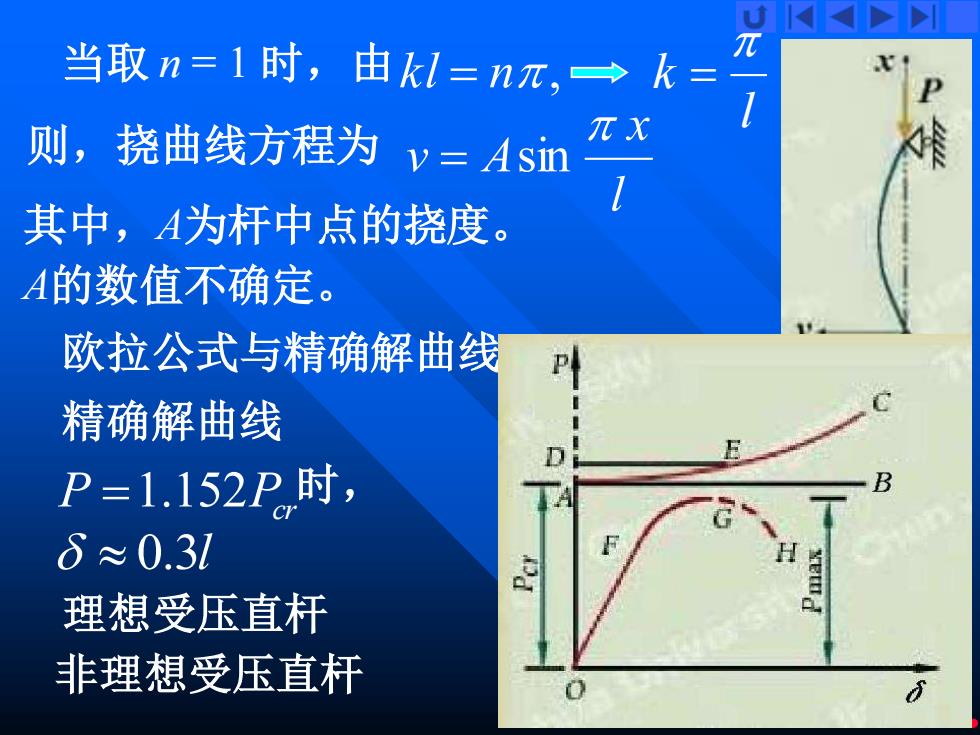
当取n=1时,由kl=n元,→k= π 则,挠曲线方程为v=Asin 元X 其中,A为杆中点的挠度。 A的数值不确定。 欧拉公式与精确解曲线 精确解曲线 P=1.152P时, δ≈0.31 理想受压直杆 非理想受压直杆
11 当 取 n = 1 时,由 kl = n , l k = 则,挠曲线方程为 lx v A = sin 其中, A为杆中点的挠度。 A的数值不确定。 欧拉公式与精确解曲线 精确解曲线 理想受压直杆 非理想受压直杆 P 152 Pcr = 1 . 0 . 3 l 时