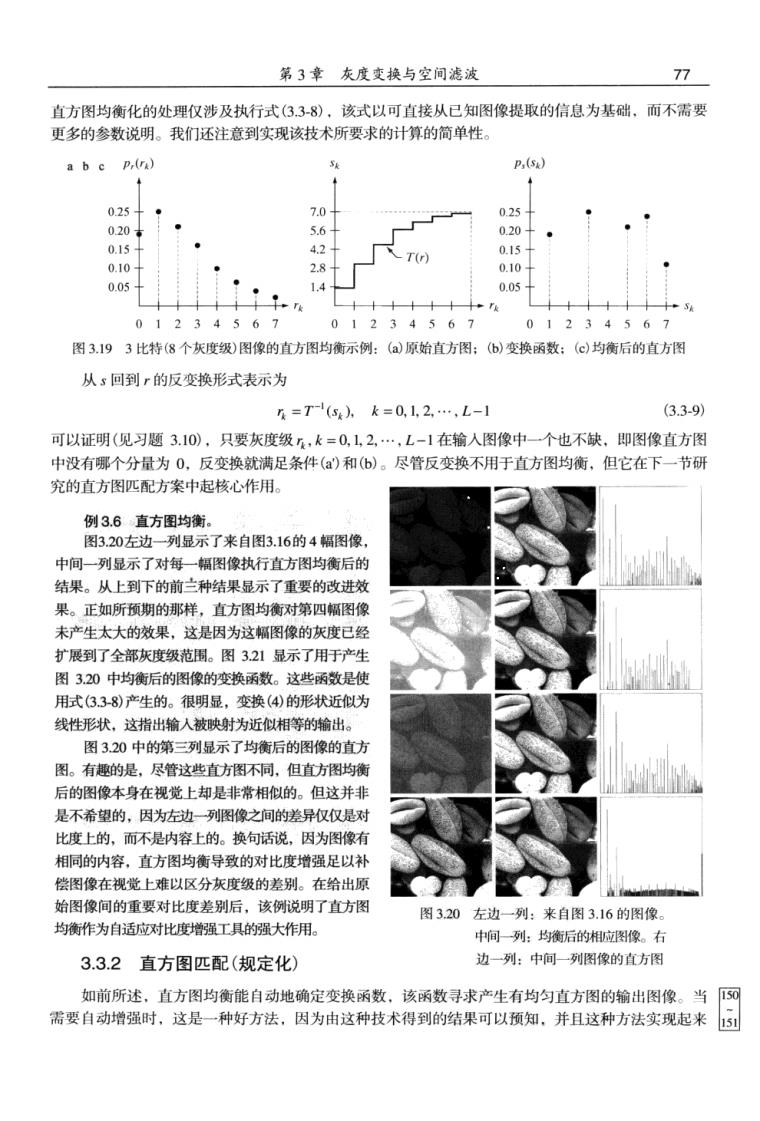
第3章灰度变换与空间滤波 直方图均衡化的处理仅涉及执行式(338》 该式以可直接从已知图像提取的信息为基础,而不需要 更多的参数说明。我们还注意到实现该技术所要求的计算的简单性。 a b c p,(ra) p() 025 7.0 025 020 5.6 0.20 0.15 4.2 0.15 -T(r) 0.10 2.8 0.10 0.05 1.4 0.05 十十十十十 十十十 十5 01234567 01234567 01234567 图3.193比特(8个灰度级)图像的直方图均衡示例:(a)原始直方图:(6)变换函数:(均衡后的直方图 从s回到r的反变换形式表示为 n=T(4,k=0,12,…,L-1 (3.3-9 可以证明(见习题3.10),只要灰度级,k=0,1,2,…,L-1在输人图像中一个也不缺,即图像直方图 中没有哪个分量为0,反变换就满足条件()和(b)。尽管反变换不用于直方图均衡,但它在下一节研 究的直方图匹配方案中起核心作用。 例3.6直方图均衡 图3.20左边一列显示了来自图3.16的4幅图修 中间一列显示了对每一幅图像执行直方图均衡后的 结果。从上到下的前兰种结果显示了重要的改进效 果。正如所预期的那样,直方图均衡对第四幅图像 未产生太大的效果,这是因为这幅图像的灰度已经 扩展到了全部灰度级范围。图321显示了用于产生 图320中均衡后的图像的变换承数。试些函数是使 用式3.38)产生的。很明显,变换(4④)的形状近似为 线性形状,这指出输人被映射为近似以相等的输出。 图3.20中的第三列显示了均衡后的图像的直方 图。有趣的是,尽管这些直方图不同,但直方图均线 后的图像本身在视觉上却是非常相似的。但这并非 是不希望的,因为左边一列图像之间的差异仅仅是对 比度上的,而不是内容上的。换句话说,因为图像有 相同的内容,直方图均衡导致的对比度增强足以补 偿图像在视觉上难以区分灰度级的差别。在给出质 始图像间的重要对比度差别后,该例说明了直方图 图320左边一列:来自图3.16的图像 均衡作为自话应对比度增强工具的强大作用 中间列:均衡后的相应图像。右 3.3.2直方图匹配(规定化) 边一列:中向一列图像的直方图 如前所述,直方图均衡能自动地确定变换函数,该函数寻求产生有均匀直方图的输出图像。当5可 需要自动增强时,这是一种好方法,因为由这种技术得到的结果可以预知,并且这种方法实现起来5
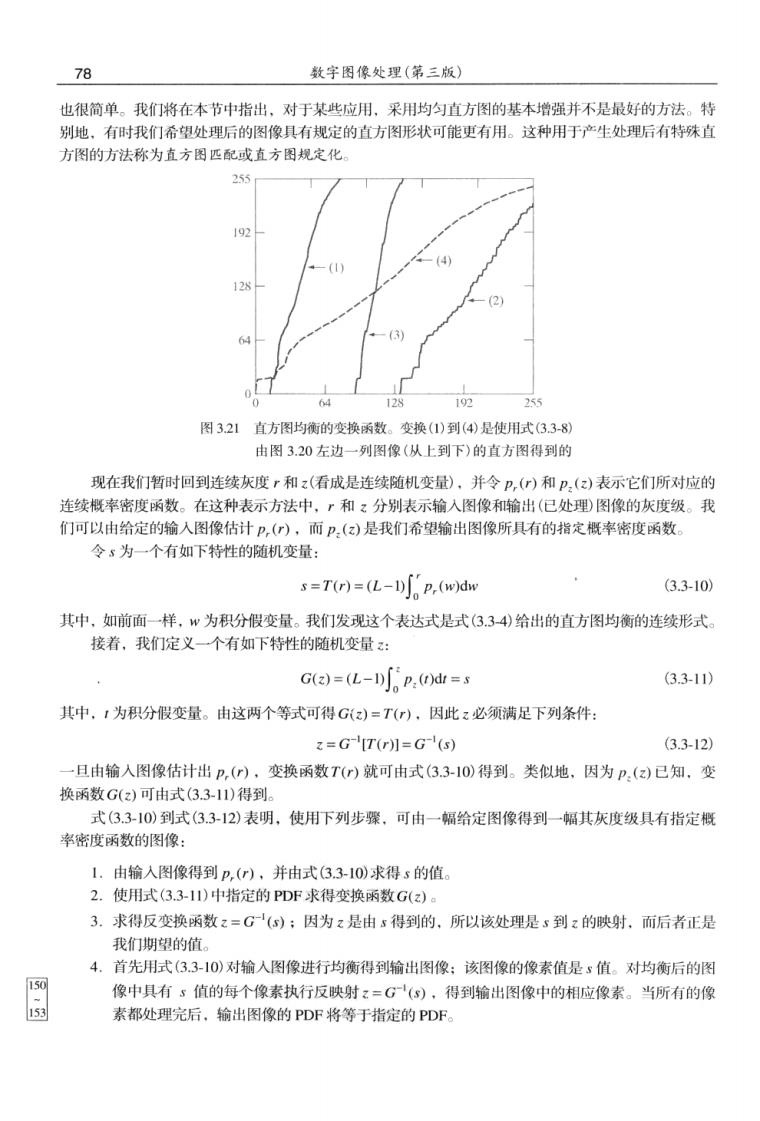
78 数字图像处理(第三斯) 也很简单。我们将在本节中指出,对于某些应用,采用均匀直方图的基本增强并不是最好的方法。特 别地。有时我们希烟处理后的图像且有规定的直方图形欣可能更有用。这种用于产生处理后有特殊直 方图的方法称为直方图匹配或直方图规定化 2 图321直方图均衡的变换函数。变换(1)到(4)是使用式(33-8) 由图3.20左边一列图像(从上到下)的直方图得到的 现在我们暂时回到连续灰度r和z(看成是连续随机变量),并令p,()和p,(:)表示它们所对应的 连续概率密度函数。在这种表示方法中,和分别表示输入图像和输出(已处理图像的灰度级。我 们可以由给定的输入图像估计P,(~),而p,(z)是我们希望输出图像所具有的指定概率密度函数 今s为一个有如下特性的随机变量: s=T(r)=(L-1)[p,(w)dw (3.3-10) 其中,如前面一样,w为积分假变量。我们发现这个表达式是式(3.34)给出的直方图均衡的连续形式 接着,我们定义一个有如下特性的随机变量: G(z)=(L-)p,)=s (33-11) 其中,,为积分假变量。由这两个等式可得G)=T(),因此z必须满足下列条件: z=G'T=G'() (33-12 一且由输入图像估计出p,(r),变换函数Tr)就可由式(3.3-10)得到。类似地,因为p,()已知,变 换函数G()可由式(3.311)得到 式(3.3-10)到式(3.312)表明,使用下列步骤.可由一幅给定图像得到一幅其灰度级具有指定概 率密度函数的图像: 1.由输入图像得到p,(),并由式3310)求得s的值 2.使用式(3.3-11)中指定的PDF求得变换函数G(z) 3.求得反变换函数z=G'(s);因为z是由s得到的,所以该处理是s到z的映射.而后者正是 我们期望的值。 4.首先用式(3.3-10)对输入图像进行均衡得到输出图像:该图像的像素值是s值。对均衡后的图 图 像中具有s值的每个像素执行反映射:=G(),得到输出图像中的相应像素。当所有的像 素都处理完后,输出图像的PDF将等于指定的PDF

第3章灰度变换与空间滤波 79 例3.7直方图规定化。 假设采用连续灰度值,并假设一幅图像的灰度PDF为p,(r)=2r(L-1)2,0≤r≤(L-),对于其他 r值有p,()=0。寻找一个变换函数,使得产生的图像的灰度PDF是p.(e)=3z2L-3,0≤z≤(L-), 而对于其他z值有p.(z)=0 首先,我们对区间0,L-】寻找直方图均衡变换 s-()--f p.(-wdw- 由定义可知,对于范围0,L-】外的值,该变换为0。输入灰度值的平方除以(亿-)将产生一幅灰度为 并具有均匀PDF的图像,因为这是早些时候讨论的直方图均衡变换。 我们感兴趣的是具有规定直方图的图像,因此,我们在0,L-】区间寻找下一个直方图均衡变换 ,3 c=u-可p.wdwL2raw- 3 由定义可知在该区间外这个函数也为0。最后,我们要求G()=s,但G()=(亿-2;因此 2亿-1)2=s,并且有 z=[(L-Is 如果我们用(亿-)乘以直方图均衡过的每一个像素,取该乘积的13次幂,结果将是一幅我们所期望的 图像,该图像在区间0,L-刂内z的灰度的PDF为P.(2)=3z2亿-1'。 因为s=r2亿-),我们可以直接由输入图像的灰度r生成: =L-023=L-12D=[-Dr273 这样,原图像中每一个像素值的平方与(亿-)相乘,然后再取该乘积的13次幂,将得到其灰度级之具有 规定PDF的图像。我《们看到,均衡输入图像的中间一步可以跳过:我们需要的是得到将,映射为s的变 换函数T)。然后,这两步可以合并为从,到z的一步变换 正如前边的例子所示,直方图规定化在原理上是简单的。在实践中,一个共同的困难是寻找 T()和G的有意义的表达式。幸运的是,在处理离散量时,向题可被大大简化。这里仅希望得到 一个近似的直方图,所以,付出的代价与直方图均衡一样。然而,不管这些,可以得到一些非常有用 的结果,尽管结果是粗糙的近似。 式(3.310)的离散形式是式(3.38)中的直方图均衡变换,为方便起见,我们重写如下: =T)=亿-2p,g=2n,k=0,2L- MN (3.3-13) 与前面一样,其中M八是图像的像素总数,m,是具有灰度值,的像素数,L是图像中可能的灰度级 数。类似地,给定一个规定的5,值,式(3.311)的离散形式涉及计算变换函数 G,)=(L-IΣp.(2) (3.3-14) 对一个q值.有 网 G(2)= (3.3-15)1

80 数字图像处理(第三版) 其中,P,(2)是规定的直方图的第i个值。与前面一样,我们用反变换找到期望的值乏,: 3。=G(s) (3.3-16) 换句话说.该操作对每一个s值给出一个z值:这样,就形成了从s到z的一个映射。 实践中,我们不需要计算G的反变换。因为我们处理的灰度级是整数(如8比特图像的灰度级是 从0到255),使用式(33-14)计算g=01,2,L-1时的所有可能G值是一件简单的事情。标定这些 值.并四舍五人为区间0,L-川内的最接近整数。将这些值存储在一个表中。然后,给定一个特殊的 5,值后,我们可以查找存储在表中的最匹配的值。例如,如果在表中第64个输入接近s,则9=63(注 意,我们是从0开始计数的),故是式(3.315)的最优解。这样,给定的s,值就与0关联在一起(即 规定的s,值将映射为,)。因为:项是用于规定的直方图P,()作为基础所用的灰度,它遵循 0=0,云=1。,211=L-1,因此,的灰度值为63。重复该过程,我们将找到每个s值到乙,值的 映射,它们是式(3.3-15)的最接近的解。这些映射也是直方图规定化问题的解。 回忆,是直方图均衡后的图像的值.我们可以总结直方图规定化过程如下: 1.计算给定图像的直方图P,(),并用它寻找式(3.313)的直方图均衡变换。把四舍五人为范 围0,L-内的整数。 2.用式(3.314)对g=0,1.2,,L-1计算变换函数G的所有值,其中p,(2)是规定的直方图的 值。把G的值四舍五人为范围0.L-]内的整数。将G的值存储在一个表中。 3.对每一个值s,k=01.2,L-1,使用步骤2存储的G值寻找相应的,值以使G(2,)最接 近,并存储这些从s到:的映射。当满足给定5,的乏,值多于一个时(即映射不唯一时),按 惯例选择最小的值。 4.首先对输入图像进行均衡,然后使用步骤3找到的映射把该图像中的每个均衡后的像素值s 映射为直方图规定化后的图像中的相应乙,值,形成直方图规定化后的图像。正如连续情况那 样,均衡输人图像的中间步骤是概念上的。它可以用合并两个变换函数T和G跳过这一步 如例3.8所示。 如早些时候提到的那样,对于满足条件()和(6)的G,G必须是严格单调的,根据式(3.3-14) 它意味着规定的直方图的任何P,()值都不能为零(见习题3.10)。当工作在离散数值的情况时,该条 件可能不满足的事实并不是一个严重的实现问题.如上面的步骤3中指出的那样。下面的例子用数字 说明了这一情况。 例3.8 一个简单例子 以便使其具有表3.2中第二列规定的值。图3,22(6)显示了该直方图的大概形状。 表3.2规定直方图和实际直方图(第三列的值来自例3.8中的计算结果) 规定的B,z》 实标的B,(Z) 8

第3章灰度变换与空间滤波 81 p.(re 030 030 025 025 020 020 015 015 010 010 005 70 025 020 015 0.10 0.05 06 图3,22(a)一幅3比特图像的直方图;(®)规定的直方图:(c)从规定的直方图 得到的变换函数:(@执行直方图规定化的结果。请比较图(b)和图(d) 过程的第一步是得到标定的直方图均衡后的值,就像在例35中那样 s0=1s2=534=6s6=7 3=3s1=6sg=7s,=7 接着,我们使用式(3.314)来计算变换函数G的所有值 G6)=7 P()=0.00 类似地,有 Ga)=7∑p.=7po)+p=00 和 Gz2)=0.00.G(z)=2.45,G(6)=5.95,G(z)=1.05,G(z)=4.55,Gz)=7.00。 如例35那样,要把这些分数值转换为有效区间0,7刀内的整数。结果是 G()=0.00→0G(z4)=2.45→2 G(z)=0.00→0G()=4.55→5 G(2)=0.00→0G(6)=5.95→6 G(3)=1.05→1G()=7.00→7 这些结果总结在表3.3中,变换函数画在图322()中。观察发现G并不是严格单调的,所以违反了条件 (:)。因此,我们使用算法的步骤3中描述的方法来处理这种情况。 在过程的第三步中,我们找到乙的最小值,所以值G(乙,)最接近。我们对悔一个值这样做,以 产生从s到z所需要的映射。例如。。=1,我们看到G(2)=1,在这种情况下,这是完美的匹配,因此 我们有对应。→。也就是说,直方图均衡后的图像中的每个值为1的像素映射为直方图规定化后的图 像中(相应位置上的值为3的像素。继续采用这一方法,我们得到表3.4中的映射 15