
72 数字图像处理(第三版) 3.3直方图处理 灰度级范围为0,L-)的数字图像的直方图是离散函数5)=m,其中万是第k级灰度值,m 是图像中灰度为的像素个数。在实践中,经常用乘积MN表示的图像像素的总数除它的每个分量来 归一化直方图,通常M和N是图像的行和列的维数。因此,归化后 的直方图由p()=n/MN给出其中k=0,1,…,L-1。简单地说。 暖。请读者 P(,)是灰度级在图像中出现的概率的一个估计。归一化直方图的 所有分量之和应等于1。 直方图是多种空间域处理技术的基础。直方图操作可用于图像增强,如本节所示。除了提供有 用的图像统计资料外,在后续章节中我们还会看到直方图中的固有信息在其他图像处理应用中也非常 有用。如图像压缩与分割。直方图在软件中计算简单,而且有助于商用硬件实现。因此已成为实时图 像处理的一种流行工具。 作为灰度变换的直方图处理的介绍.我们考虑图3.16,它是图3.10所示的以4个基本灰度级为特征 的花粉图像:暗图像、亮图像、低对比度图像和高对比度图像。图的右侧显示了与这些图像对应的直方 图。每个直方图的水平轴对应于灰度值,,垂直轴对应于值h(,)=,或的一化后的值p()=m4/MW 这样,方图就可以简单地被看成是()=对应于或p)=/MN对应于的图形 我们注意到,在暗图像中,直方图的分量集中在灰度级的低(暗)端。类似地,亮图像直方图的 分量则倾向于灰度级的高端。低对比度图像具有较窄的直方图.。且集中于灰度级的中部。对于单色图 像。这意味着暗淡。好像灰度被冲淡了一样。最后,我们看到高对比度图像中直方图的分量覆盖了 很宽的灰度级范围,而且像素的分布没有太不均匀,只有少量垂线比其他的高许多。直观上,可以得 出这样的结论:若一幅图像的像素倾向于占据整个可能的灰度级并且分布均匀,则该图像会有高对比 度的外观并展示灰色调的较大变化。最终效果将是一幅灰度细节丰富且动态范围较大的图像。很快将 会证明,仅仅依靠输入图像直方图中的可用信息就可开发出一个变换函数来自动地实现这种效果。 3.3.1直方图均衡 考虑连续灰度值。并用变量r表示待处理图像的灰度。通常,我们假设r的取值区间为0,L-】 且r=0表示黑色,「=L-1表示白色。在r满足这些条件的情况下,我们将注意力集中在变换形式 s=T(r.0≤r≤L-1 (3.3-1 上(灰度映射),对于输入图像中每个具有,值的像素值产生一个输出灰度值5。我们假设 (a)T)在区间0≤r≤L-1上为单调递增函数 (b)当0≤r≤L-1时,0≤T(r)≤L-1。 在稍后讨论的一些公式中,我们用反函数 r=T(s.0≤s≤L-】 (3.3-2) 在这种情况下,条件(a)改为 (a')T()在区间0≤r≤L-1上是一个严格单调递增函数 图 ①如果对于5>行有TG)≥T行),则称函数T)是单调递增的.如果对于5>5有T5)>T),则将函数T)是严格单剥 递增的。类似的定义适用于单调递减函数
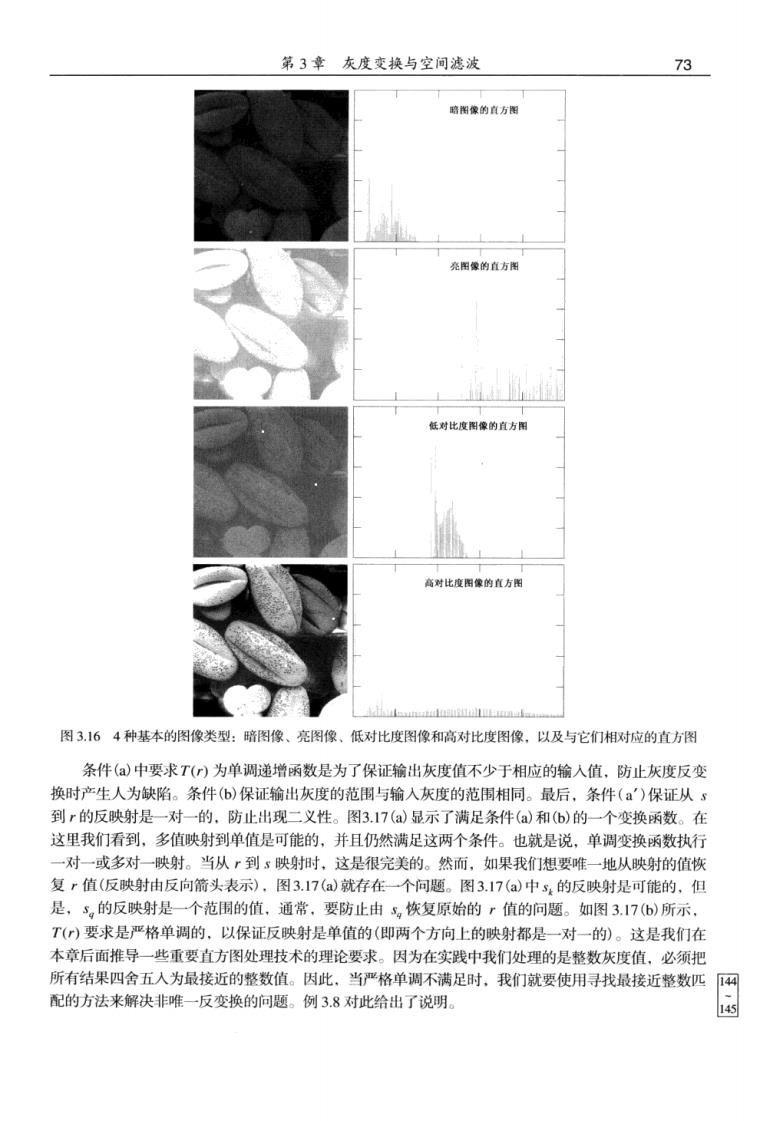
第3章灰度变换与空间滤波 73 围图象的直方图 亮用像的直方图 低对比度用像的直方闲 高对比度图像的直方用 图3,164种基本的图像类型:暗图像、亮图像、低对比度图像和高对比度图像,以及与它们相对应的直方图 条件(a)中要求T)为单调递增函数是为了保证输出灰度值不少于相应的输入值,防止灰度反变 换时产生人为缺陷。条件(6)保证输出灰度的范围与输入灰度的范围相同。最后,条件(a')保证从S 到r的反映射是一对一的,防止出现二义性。图3.17()显示了满足条件(a和b)的一个变换函数。在 这里我们看到,多值映射到单值是可能的,并且仍然满足这两个条件。也就是说,单调变换函数执行 一对一或多对一映射。当从,到s映射时,这是很完美的。然而,如果我们想要唯一地从映射的值恢 复r值(反映射由反向箭头表示),图3.17(a就存在一个问题。图3.17(a)中s的反映射是可能的,但 是,5的反映射是一个范围的值.通常,要防止由恢复原始的r值的问题。如图3.176)所示, T()要求是严格单调的,以保证反映射是单值的(即两个方向上的映射都是一对一的)。这是我们在 本章后面推导一些重要直方图处理技术的理论要求。因为在实践中我们处理的是整数灰度值、必须把 所有结果四舍五入为最接近的整数值。因此。当严格单调不满足时,我们就要使用寻找最接近整数匹 配的方法来解决非唯一反变换的问题。例3.8对此给出了说明
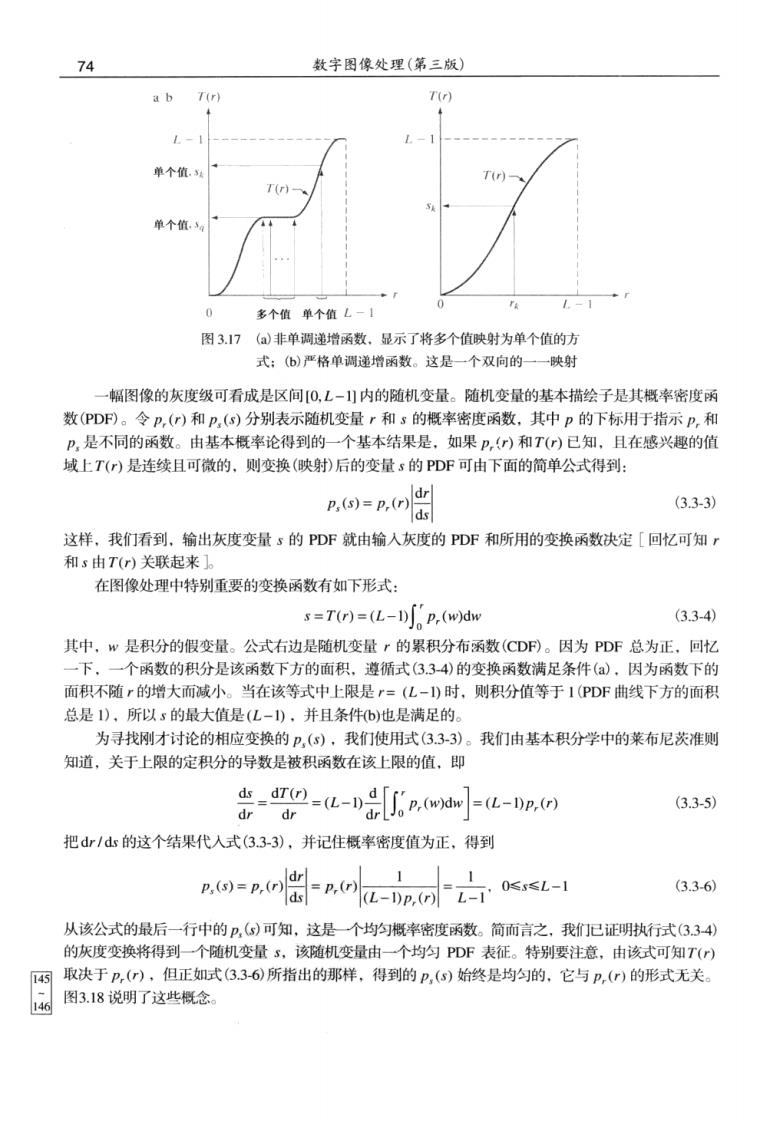
74 数字困像处理(第三版) ab -1 单个值 T)- T(r) 单个值 0多个值单个值L-1 图3.17(a)非单调递增函数。显示了将多个值映射为单个值的方 式:(⑥)严格单调递增函数。这是一个双向的一一映射 一幅图像的灰度级可看成是区间0,L-]内的随机变量。随机变量的基本描绘子是其概率密度函 数(PDF)。令p,()和p,(s)分别表示随机变量r和s的概率密度函数.其中p的下标用于指示p,和 p,是不同的函数。由基本概率论得到的一个基本结果是,如果p,)和T)已知,且在感兴趣的值 域上T()是连续且可微的,则变换(映射)后的变量s的PDF可由下面的简单公式得到: p.O-p.( (3.3-3) 这样,我们看到,输出灰度变量s的PDF就由输入灰度的PDF和所用的变换函数决定[回忆可知, 和s由T(r)关联起来]。 在图像处理中特别重要的变换函数有如下形式: s=T(r)=(L-I)['p,(w)dw (3.3-4) 其中,w是积分的假变量。公式右边是随机变量r的累积分布函数(CDF)。因为PDF总为正,同忆 一下,一个函数的积分是该函数下方的面积,遵循式(334)的变换函数满足条件(a,因为函数下的 面积不随r的增大而减小。当在该等式中上限是r=(亿-)时,则积分值等于1(PDF曲线下方的面积 总是1),所以s的最大值是(L-),并且条件b)也是满足的。 为寻找刚才讨论的相应变换的P,(s),我们使用式(3.33)。我们由基本积分学中的菜布尼茨准则 知道,关于上限的定积分的导数是被积函数在该上限的值,即 p.w-(-Dp.() 3.35) dr dr 把d/山的这个结果代入式(3.33),并记住概率密度值为正,得到 a-n() (L-DP,(L-T 05xSL-1 (3.36) 从该公式的最后一行中的,(s)可知,这是一个均匀概率密度函数。简而言之,我们已证明执行武(3.34) 的灰度变换将得到一个随机变量s,该随机变量由一个均匀PDF表征。特别要注意,由该式可知T() 固a 取决于p,(),但正如式33-6)所指出的那样,得到的p,()始终是均匀的.它与p,()的形式无关

第3章灰度变换与空间滤波 75 a b p.(r) +式334)+ 图3.18(a)一个任意的PDF:(b)对所有灰度级r应用式(334)中的变 换的结果。具有均的PDF的结果灰度与r的PDF的形式无关 例3.4式(3.34)和式(3.3-6)的说明 为牢记这一概念, 考虑下面这个简单的例子。假设图像中的(连续)灰度值有如下PDF 2r p,=亿- 0sr<L-1 0. 其他 从式(334)有 T()-f p.(dw 假设我们接着使用这个变换得到一幅灰度为s的新图像:也就是说,s值是通过求输人图像的相应灰度值 的平方,然后除以(亿-)形成的。例如,考虑一幅L=10的图像,并且假设输入图像中任意位置(x,y)处 的像素有灰度r=3。则新图像中在该位置的像素是s=T)=子/9=1。我们可以把p,()代人式(3.3-6), 并用s=己亿-)这样的事实验证新图像中的灰度的PDF是均匀的,即 其中,最后一步遵循了这样一个事实,即,是非负的并且假设L>1。正如所期望的那样,结果是一个均 匀的PDF 对于离散值,我们处理其概率(直方图值与求和来替代处理概率密度函数与积分。正如前面提 到的那样,一幅数字图像中灰度级出现的概率近似为 Pm)=k=012,L- (3.3-7) 其中,MN是图像中像素的总数.几,是灰度为的像素个数,L是图像中可能的灰度级的数量(即对8比 特图像是256)。正像本节开始说明的那样,与:相对的P,(:)图形通常称为直方图。 式(3.34)中变换的离散形式为 (3.3-8 ①先前声明的单调性条件同样适用于离散情形。我们简单地将变量的值限制为离散值

76 数字困像处理(第三版) 这样,已处理的图像(即输出图像)通过式(3.38)将输入图像中灰度级为,的各像素映射到输出图像中 灰度级为的对应像素得到。在这个公式中,变换(映射)T)称为直方图均街或直方图线性变换 不难证明(见习题3.10)该变换函数满足本节前面所述的条件(a)和(b)。 例3.5直方图均衡的简单说明 在继续之前,通过一个简单的例子来说明直方图均衡的工作原理是有帮助的。假设一幅大小为 64×64像素(MN=4096)的3比特图像亿=8)的灰度分布如表3.1所示,其中灰度级是范围0,L】=[Q,刀 中的整数。 表3.1大小为64×64像素的3比特数字图像的灰度分布和直方图值 pAr)n./MN 假设图像的直方图如图3.19(a)所示。直方图均衡变换函数的值使用式(3.38》得到。例如, 0=To)=7∑P,g)=7p,6)=1.33 类似地,有 与=T0=7交n=76+7W=38 及2=4.55,3=5.67,54=6.23,=6.65,56=6.86,s与=7.00。该变换函数的形状为阶梯形状,如图3.19b) 所示。 在这一点上,s值一直是分数,因为它们是通过求概率值的和产生的,因此我们要把它们近似为最接近 的整数: 0=1.33→154=6.23→6 =3.08→3 5=6.65→7 52=4.55.→556=6.86-→7 51=5.67→652=7.00→7 这些是均衡后的直方图的值。很明显,只有5个不同的灰度级。因为=0被映射为0=1,在均衡后的 图像中有790个像素具有该值(见表3.1)。另外,在图像中有1023个像素取5=3这个值.有850个像素 取2=5这个值。然而,,和,都被映射为同-个值6,所以在均衡后的图像中有(656+329=985个像素 取这个值。类似地,在均衡后的图像中有(245+122+81)=448个像素取7这个值。使用MN=4096除这 些数就得到了图3.19(。)所示的均衡后的直方图。 因为直方图是PD℉的近似,而且在处理中不允许造成新的灰度级,所以在实际的直方图均衡应用中, 很少见到完美平坦的直方图。因此,不像连续的情况,通常不能证明离散直方图均衡会导致均匀的直方 图。然面,正像您将很快看到的那样,式(3.3-8)具有展开输入图像直方图的趋势,均衡后的图像的灰度 级跨越更宽灰度级范围。最终结果是增强了对比度。 圆之纪财还有个,时吧北光全的,热的 在本节前面,讨论了具有覆盖整个灰度范围的灰度值的许多优点。除了产生有这样的趋势的灰