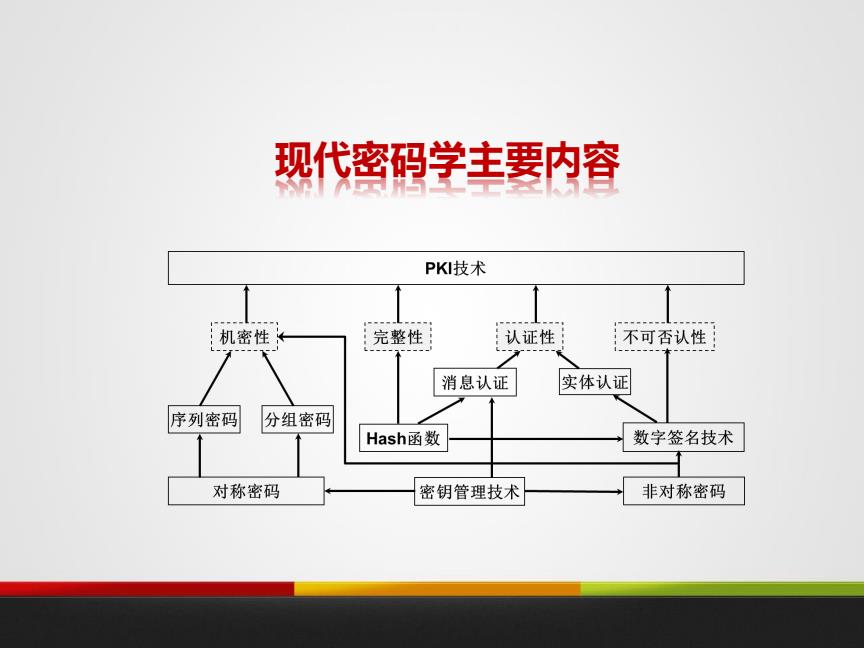
现代密码学主要内容 PKI技术 机密性女 完整性 认证性 不可否认性 消息认证 实体认证 序列密码 分组密码 Hash函数 数字签名技术 对称密码 密钥管理技术 非对称密码
现代密码学主要内容
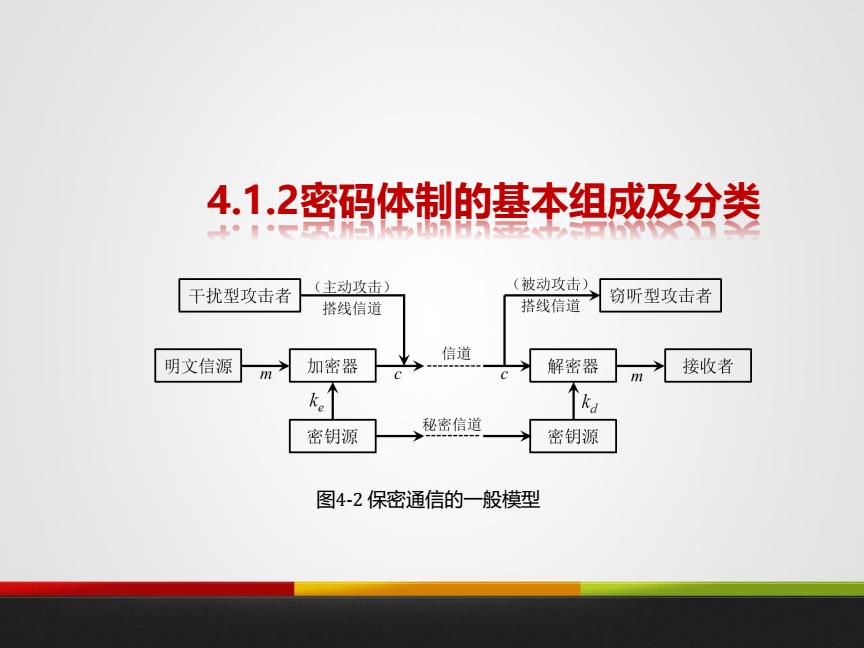
4.1.2密码体制的基本组成及分类 干扰型攻击者 (主动攻击) (被动攻击) 搭线信道 窃听型攻击者 搭线信道 信道 明文信源 m 加密器 解密器 接收者 m k. 密钥源 秘密信道 密钥源 图4-2保密通信的一般模型
4.1.2密码体制的基本组成及分类 图4-2 保密通信的一般模型

密码体制的组成 一个密码体制(cryptosystem)由五个部分组成: √明文空间M,它是全体明文m的集合; √密文空间C,它是全体密文c的集合 密钥空间K,它是全体密钥的集合。其中每一个密钥k均由加密密钥k和解密密钥k,组 成,即k=(ke,ka); 加密算法E,是在密钥控制下将明文消息从M对应到C的一种变换,即c=E(k。,m); 解密算法D,是在密钥控制下将密文消息从C对应到M的一种变换,即m=D(k,c)
密码体制的组成 一个密码体制(cryptosystem)由五个部分组成: 明文空间M,它是全体明文m 的集合; 密文空间C,它是全体密文c 的集合; 密钥空间K,它是全体密钥k的集合。其中每一个密钥k 均由加密密钥ke和解密密钥kd 组 成,即k = (ke , kd ); 加密算法E,是在密钥控制下将明文消息从M 对应到C 的一种变换,即c = E (ke , m ); 解密算法D,是在密钥控制下将密文消息从C 对应到M 的一种变换,即m =D (kd , c )
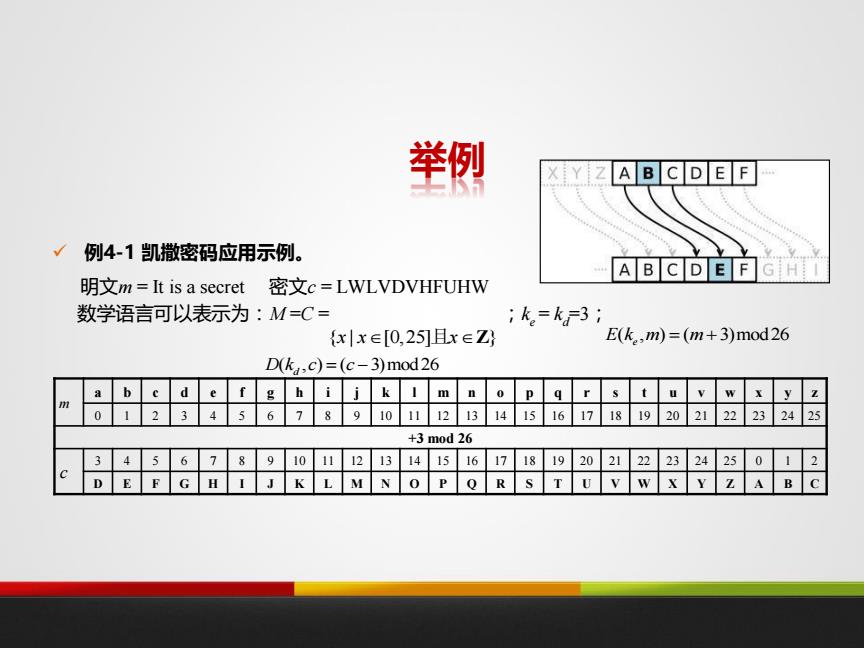
举例 X Y ZA B C D E F 例4-1凯撒密码应用示例。 ABCDEFGH 明文m=It is a secret密文c=LWLVDVHFUHW 数学语言可以表示为:M=C= ;k=k3 {x|x∈[0,25]且x∈Z E(k.,m)=(m+3)mod26 D(k,c)=(c-3)mod26 a bc d e f g h i j k 1 m n o p q r s t u v w xy z 0 123456789101112131415 16171819202122232425 +3m0d26 89 10 1112 13 1415 1617 1819202122232425 01 2 D H K L M N 0 R T U V W X Y Z A B C
举例 例4-1 凯撒密码应用示例。 明文m = It is a secret 密文c = LWLVDVHFUHW 数学语言可以表示为:M =C = ;ke = kd =3; { | [0,25] } x x x 且 Z ( , ) ( 3)mod26 E k m m e ( , ) ( 3)mod26 D k c c d m a b c d e f g h i j k l m n o p q r s t u v w x y z 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 +3 mod 26 c 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 0 1 2 D E F G H I J K L M N O P Q R S T U V W X Y Z A B C

举例 √例4-2 Vernam密码应用示例。 在对明文加密前,首先将明文编码为(0,1)序列,加密时用 明文与密钥进行模2相加,解密时将密文再与密钥模2相加即可。 1000111000 例如:明文为1000111000,密钥为1001000101时,加密得到 1001000101 的密文为0001111101。 0001111101 在应用/ernam密码时,如果每次使用不同的随机密钥对明文 进行加密,则被称为一次一密(one-time pad,OTP)密码
举例 例4-2 Vernam密码应用示例。 在对明文加密前,首先将明文编码为(0,1)序列,加密时用 明文与密钥进行模2相加,解密时将密文再与密钥模2相加即可。 例如:明文为10001 11000,密钥为10010 00101时,加密得到 的密文为00011 11101。 在应用Vernam密码时,如果每次使用不同的随机密钥对明文 进行加密,则被称为一次一密(one-time pad, OTP)密码。 10001 11000 10010 00101 00011 11101